Тема 3.4. Производная по направлению
Пусть в плоскости XOY расположена точка M0(x0,y0). Зададим произвольный угол a и рассмотрим множество точек на той же плоскости, координаты которых определяются из формул
x = x0 + t cosa, y = y0 + t sina. (3.4.1)
Здесь t ‑ параметр, который может быть равен любому числу. Из формул (3.4.1) следует:
(y - y0)/(x - x0) = tga
Это означает, что все точки M(x,y), координаты которых удовлетворяют равенствам (3.4.1), лежат на прямой, проходящей через точку M0(x0,y0) и составляющей угол a с осью OX. Каждому значению t соответствует единственная точка M(x,y), лежащая на этой прямой, причем согласно формуле (3.4.1) расстояние между точками M0(x0,y0) и M(x,y) равно t. Можно считать эту прямую числовой осью с положительным направлением, определяемым возрастанием параметра t. Обозначим положительное направление этой оси символом l.
Производной функции z = f(x,y) в точке M0(x0,y0)по направлению l называется число
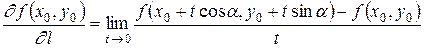 . (3.4.2)
. (3.4.2)
Производной функции по направлению можно дать геометрическую интерпретацию. Если через прямую l, определяемую формулами (3.4.1), провести вертикальную плоскость P (на самом деле в трехмерном пространстве уравнения (3.4.1) определяют эту самую плоскость), то эта плоскость пересечет поверхность-график функции z = f(x,y)вдоль
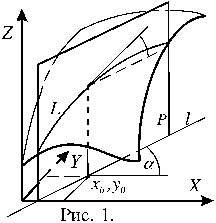 |
некоторой пространственной кривой L. Тангенс угла между горизонтальной плоскостью и касательной к этой кривой в точке M0(x0,y0)равен производной функции в этой точке по направлению l.
 В любом курсе математического анализа доказывается, что производная по направлению, определяемая формулой (3.4.2), может быть представлена в виде
В любом курсе математического анализа доказывается, что производная по направлению, определяемая формулой (3.4.2), может быть представлена в виде
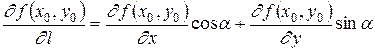 . (3.4.3) (3)
. (3.4.3) (3)
Заметим, что частная производная по x тоже является производной по направлению. Это направление определяется равенствами: cosa = 1; sina = 0. Аналогично частная производная по y — это производная по направлению, которое можно задать условиями cosa = 0; sina = 1.
Прежде, чем анализировать формулу (3.4.3), приведем некоторые понятия и факты из курса векторной алгебры. Пусть в плоскости с системой координат XOY задан направленный отрезок 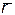 или (что то же самое) вектор, причем точка M0(x0,y0)является его начальной точкой, а M1(x1,y1)‑ конечной точкой. Определим координату вектора по оси OX как число, равное x1 ‑ x0, а координату по оси
или (что то же самое) вектор, причем точка M0(x0,y0)является его начальной точкой, а M1(x1,y1)‑ конечной точкой. Определим координату вектора по оси OX как число, равное x1 ‑ x0, а координату по оси 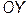 , как число, равное y1 ‑ y0. Если задать упорядоченную пару любых чисел a и b, то эти числа можно рассматривать как координаты некоторого вектора
, как число, равное y1 ‑ y0. Если задать упорядоченную пару любых чисел a и b, то эти числа можно рассматривать как координаты некоторого вектора 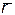 в плоскости XOY, причем длина этого вектора определена формулой
в плоскости XOY, причем длина этого вектора определена формулой
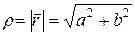 ,
,
а тангенс угла наклона g вектора к оси OX определяется из формулы tgg = b/a (отметим, что зная величину tgg , а также знак любого из чисел a и b, мы можем определить угол g с точностью до 2p ).
Представление вектора в виде пары его координат будем записывать в виде 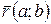 или
или 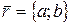 . Такое представление имеет одну характерную особенность: оно не определяет местоположение вектора на плоскости XOY. Чтобы его определить, нужно наряду с координатами вектора задавать, например, координаты его начальной точки или, как её можно назвать, точки приложения вектора.
. Такое представление имеет одну характерную особенность: оно не определяет местоположение вектора на плоскости XOY. Чтобы его определить, нужно наряду с координатами вектора задавать, например, координаты его начальной точки или, как её можно назвать, точки приложения вектора.
Если заданы два вектора: 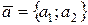 и
и 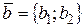 , то скалярным произведением
, то скалярным произведением 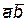 этих векторов называется число
этих векторов называется число 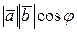 (j‑ угол между векторами).
(j‑ угол между векторами).
В любом курсе векторной алгебры доказывается, что скалярное произведение векторов 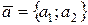 и
и 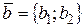 равно сумме произведений одноименных координат этих векторов:
равно сумме произведений одноименных координат этих векторов:
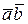 = a1b1 + a2b2. (3.4.4)
= a1b1 + a2b2. (3.4.4)
Пусть в некоторой области G плоскости XOYзадана функция z = f(x,y), имеющая непрерывные частные производные по обоим аргументам. Градиентом или вектором-градиентом 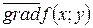 функции f(x,y) в точке (x,y) Î G называется вектор, который задается формулой
функции f(x,y) в точке (x,y) Î G называется вектор, который задается формулой
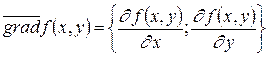 .
.
Функция f определяет для каждой точки области G вектор-градиент, исходящий из этой точки.
Возвратимся теперь к формуле (3.4.3). Ее правую часть мы можем рассматривать, как скалярное произведение векторов. Первый из них ‑ вектор-градиент функции z = f(x,y)в точке M0(x0,y0):
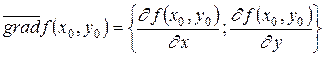 .
.
Второй – вектор 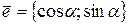 . Это вектор, имеющий длину 1 и угол наклона к оси
. Это вектор, имеющий длину 1 и угол наклона к оси 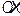 , равный a.
, равный a.
Теперь можно сделать вывод, что производная функции z = f(x,y)по направлению, определяемому углом a наклона к оси OX, в точке M0(x0,y0) может быть вычислена по формуле
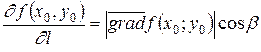 . (3.4.5)
. (3.4.5)
Здесь b ‑ угол между вектором 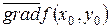 и вектором
и вектором 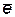 , задающим направление, по которому берется производная. Здесь также учтено, что
, задающим направление, по которому берется производная. Здесь также учтено, что 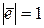 .
.
Из формулы (3.4.5) можно сделать очень важное заключение: производная по направлению от функции z = f(x,y) в точке M0(x0,y0)достигает наибольшего значения, если это направление совпадает с направлением вектора-градиента функции в рассматриваемой точке, так как cosb £1, и равенство достигается только если b = 0 (очевидно, что другие решения уравнения cosb = 1 нас в данном случае не интересуют). Иначе можно сказать, что вектор-градиент функции в точке направлен в сторону наискорейшего возрастания функции в этой точке.
Кроме того из формулы (3.4.5) следует, что наибольшее значение производной по направлению в точке или наибольшее значение скорости возрастания функции в точке равно длине вектора-градиента функции в этой точке.
Пример. Требуется найти производную функции 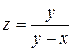 по направлению, составляющему угол в 60° с осью OX, в точке (1;3).
по направлению, составляющему угол в 60° с осью OX, в точке (1;3).
Найдем частные производные функции: 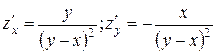 Теперь можно определить градиент функции в точке (1;3):
Теперь можно определить градиент функции в точке (1;3): 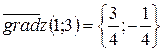 . Принимая во внимание равенство
. Принимая во внимание равенство 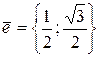 , воспользуемся формулой (3.4.4):
, воспользуемся формулой (3.4.4):
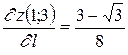 .
.
