Определение функции положения и кинематических характеристик выходного звена механизма
Рассмотрим механизм, изображенный на рис. 30. Размеры звеньев механизма и закон движения кривошипа приведены в таблице 2.
Таблица 2
| lOA , м | lO1O , м | lO1B , м | Закон движения кривошипа 1, рад | ω, рад/с |
| 0.1 | 0.3 | 0.6 | φ = ωt | 4 |
Построим план положений механизма в масштабе 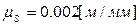 . За нулевое примем крайнее правое положение механизма; траектория точки A кривошипа 1 будет отображаться на плане положений окружностью радиуса
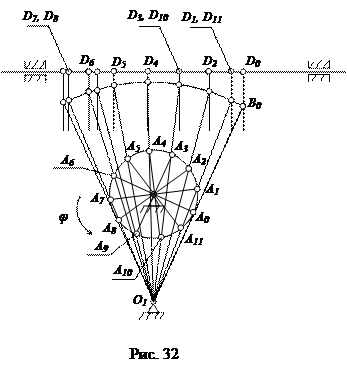
. За нулевое примем крайнее правое положение механизма; траектория точки A кривошипа 1 будет отображаться на плане положений окружностью радиуса 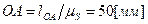 . Разделив эту окружность на 12 равных частей, начиная от нулевого положения, выполним построение кинематической схемы механизма в соответствующих 12 положениях. Положения механизма нумеруются в соответствии с направлением вращения кривошипа 1. Все построения выполняются на миллиметровой бумаге, размер которой соответствует формату А2. Результат построений приведен на рис. 32. План положений позволяет визуально оценить взаимное расположение звеньев при движении механизма, определить его крайние положения и диапазон перемещения выходного звена. На основе плана положений определяется график функции положения механизма, выполняется построение планов скоростей и ускорений, а также силовой анализ.
. Разделив эту окружность на 12 равных частей, начиная от нулевого положения, выполним построение кинематической схемы механизма в соответствующих 12 положениях. Положения механизма нумеруются в соответствии с направлением вращения кривошипа 1. Все построения выполняются на миллиметровой бумаге, размер которой соответствует формату А2. Результат построений приведен на рис. 32. План положений позволяет визуально оценить взаимное расположение звеньев при движении механизма, определить его крайние положения и диапазон перемещения выходного звена. На основе плана положений определяется график функции положения механизма, выполняется построение планов скоростей и ускорений, а также силовой анализ.
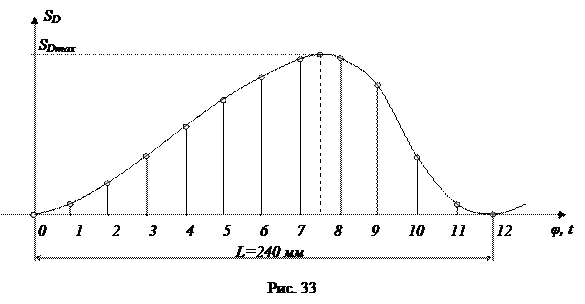
Построим функцию положения механизма. На оси абсцисс отложим отрезки по 20 мм, соответствующие поворотам кривошипа 1 на каждые 300. Все 12 положений (полный оборот кривошипа) займут отрезок L = 240 мм. Вдоль оси ординат отложим отрезки, соответствующие положениям точки D суппорта 5 относительно ее нулевого положения. Результат построений приведен на рис. 33.
 | |||
 |
Вычислим масштаб, в котором отложен угол φ поворота кривошипа 1: 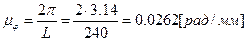 . Масштаб времени t:
. Масштаб времени t: 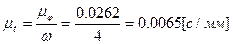 . Таким образом, изображенный на рис. 4 график является не только функцией положения механизма S(φ), но и законом движения S(t) суппорта 5. Такое совмещение справедливо только для случая равномерного вращения кривошипа 1 в установившемся режиме.
. Таким образом, изображенный на рис. 4 график является не только функцией положения механизма S(φ), но и законом движения S(t) суппорта 5. Такое совмещение справедливо только для случая равномерного вращения кривошипа 1 в установившемся режиме.
Найдем скорость VD суппорта 5 графическим методом. Так как скорость точки является производной по времени от ее перемещения, т.е. 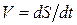 , то задача построения графика скорости точки D сводится к дифференцированию графика перемещения SD(t) по времени t. Для выполнения операции графического дифференцирования используем метод хорд. Этот метод основан на геометрическом смысле полной производной функции одного аргумента, которая определяется как тангенс угла наклона касательной, проведенной к графику функции в некоторой точке, к оси абсцисс. В методе хорд касательные заменяются хордами – прямолинейными отрезками, соединяющими соседние точки графика функции. Порядок дифференцирования методом хорд состоит в следующем.
, то задача построения графика скорости точки D сводится к дифференцированию графика перемещения SD(t) по времени t. Для выполнения операции графического дифференцирования используем метод хорд. Этот метод основан на геометрическом смысле полной производной функции одного аргумента, которая определяется как тангенс угла наклона касательной, проведенной к графику функции в некоторой точке, к оси абсцисс. В методе хорд касательные заменяются хордами – прямолинейными отрезками, соединяющими соседние точки графика функции. Порядок дифференцирования методом хорд состоит в следующем.
· Гладкая кривая графика перемещения заменяется ломаной линией, составленной из хорд.
· На оси абсцисс графика скорости, влево от начала отсчета, откладывается вспомогательный отрезок k, длина которого выбирается произвольно (рекомендуется k = 30 мм).

·
· От конца отрезка k откладываются прямые, параллельные соответствующим хордам. Эти прямые проводятся до пересечения с осью ординат графика скорости. Точка пересечения переносится на вертикальную линию, разделяющую хорду пополам.
· Полученные таким образом точки графика скорости соединяются плавной кривой.
· Отрезки на оси абсцисс графика перемещения 0 – 1, 1 – 2, и т.д., делятся пополам вертикальными линиями.
Результат выполнения указанных операций приведен на рис. 34. Стрелкой показан параллельный перенос хорды при построении графика скорости. Масштаб скорости 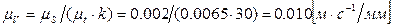 . Для того, чтобы вычислить значение скорости точки D в какой-либо момент времени, достаточно определить по графику VD(t) ординату и умножить ее на μV.
. Для того, чтобы вычислить значение скорости точки D в какой-либо момент времени, достаточно определить по графику VD(t) ординату и умножить ее на μV.
Ускорение точки D определяется аналогично, путем дифференцирования графика скорости (рис. 6). Если операция графического дифференцирования выполняется без применения компьютерных средств автоматизации, то, как правило, точность определения ускорения оказывается невысокой.
 |
Масштаб ускорения 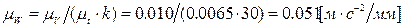 .
.
Таким образом, на основе плана положений получены искомые кинематические диаграммы перемещения, скорости и ускорения суппорта строгального станка.
4.2. Построение планов скоростей и ускорений
 |
Обозначим A1 точку A, принадлежащую кривошипу 1, а точку A, принадлежащую кулисе 3, обозначим A3. Тогда, по теореме о сложении скоростей, можно записать:
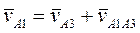 , (1)
, (1)
где 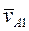 - абсолютная скорость точки A, принадлежащей кривошипу 1,
- абсолютная скорость точки A, принадлежащей кривошипу 1, 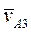 - скорость точки A, принадлежащей кулисе 3 (переносная скорость),
- скорость точки A, принадлежащей кулисе 3 (переносная скорость), 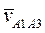 - скорость точки A кривошипа 1 относительно точки A кулисы 3 (относительная скорость). Найдем
- скорость точки A кривошипа 1 относительно точки A кулисы 3 (относительная скорость). Найдем 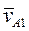 :
: 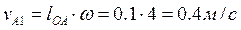 , направление вектора
, направление вектора 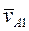 - перпендикуляр к OA в сторону вращения кривошипа 1. Скорости
- перпендикуляр к OA в сторону вращения кривошипа 1. Скорости 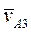 и
и 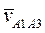 известны только по направлению:
известны только по направлению: 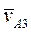 - перпендикуляр к O1B,
- перпендикуляр к O1B, 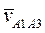 - вдоль O1B. Поэтому, для вычисления величин этих векторов удобно воспользоваться методом векторных планов. Из произвольной точки pv, называемой полюсом плана скоростей, отложим отрезок pva1 произвольной длины, отображающий абсолютную скорость
- вдоль O1B. Поэтому, для вычисления величин этих векторов удобно воспользоваться методом векторных планов. Из произвольной точки pv, называемой полюсом плана скоростей, отложим отрезок pva1 произвольной длины, отображающий абсолютную скорость 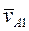 (рис. 9). В данном случае pva1= 36 мм. Тогдамасштаб плана скоростей
(рис. 9). В данном случае pva1= 36 мм. Тогдамасштаб плана скоростей 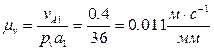 . Согласно векторному уравнению (1) через точку a1 проведем прямую, параллельную O1B (направление скорости
. Согласно векторному уравнению (1) через точку a1 проведем прямую, параллельную O1B (направление скорости 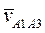 ) и через точку pv – прямую, перпендикулярную O1B (направление
) и через точку pv – прямую, перпендикулярную O1B (направление 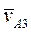 ). На пересечении этих прямых получим точку a3.
). На пересечении этих прямых получим точку a3.
 | |||
 | |||
Рассмотрим теперь движение суппорта 5 и кулисы 3. Согласно теореме о сложении скоростей, имеем:
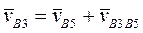 , (2)
, (2)
где 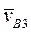 - абсолютная скорость точки B, принадлежащей кулисе 3,
- абсолютная скорость точки B, принадлежащей кулисе 3, 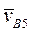 - абсолютная скорость точки B, принадлежащей суппорту 5 (переносная скорость),
- абсолютная скорость точки B, принадлежащей суппорту 5 (переносная скорость), 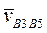 - скорость точки B, принадлежащей кулисе 3 относительно точки B, принадлежащей суппорту 5. Отложим от точки pv в направлении pva3 отрезок
- скорость точки B, принадлежащей кулисе 3 относительно точки B, принадлежащей суппорту 5. Отложим от точки pv в направлении pva3 отрезок 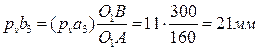 , отображающий на плане скорость
, отображающий на плане скорость 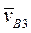 (рис. 37). Длины отрезков O1A и O1B (мм) измеряются на плане положений механизма. Через точку b3, согласно (2), проведем прямую по направлению скорости
(рис. 37). Длины отрезков O1A и O1B (мм) измеряются на плане положений механизма. Через точку b3, согласно (2), проведем прямую по направлению скорости 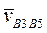 и замкнем треугольник прямой, проведенной в направлении скорости
и замкнем треугольник прямой, проведенной в направлении скорости 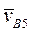 . На пересечении этих прямых отметим точку b5. План скоростей для данного положения механизма выполнен. Теперь интересующие нас скорости звеньев найдем, измеряя отрезки на плане скоростей и умножая полученные значения на масштаб плана скоростей:
. На пересечении этих прямых отметим точку b5. План скоростей для данного положения механизма выполнен. Теперь интересующие нас скорости звеньев найдем, измеряя отрезки на плане скоростей и умножая полученные значения на масштаб плана скоростей:
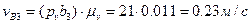 ,
,
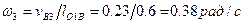 ,
,
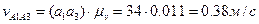 ,
,
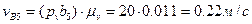 .
.
Таким образом, скорость суппорта 5 в положении, указанном на рис. 8, равна 0.22 м/с и направлена влево. Полученный результат соответствует исходным данным: действительно, согласно положению механизма на схеме, крайнее правое положение суппортом уже пройдено и он движется справа налево.
Определим ускорения звеньев механизма. По теореме о сложении ускорений можно записать:
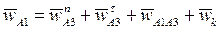 , (3)
, (3)
где 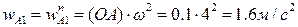 (
( 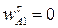 , так как
, так как 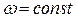 );
); 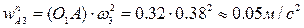 ,
, 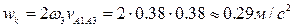 . Таким образом, в уравнении (3) присутствуют два неизвестных по величине ускорения; для их вычисления воспользуемся методом векторных планов. Отложим от полюса плана ускорений pw отрезок pwa1, изображающий ускорение точки A кривошипа 1 (рис. 38). Длину этого отрезка примем равной 40 мм. Тогда масштаб плана ускорений
. Таким образом, в уравнении (3) присутствуют два неизвестных по величине ускорения; для их вычисления воспользуемся методом векторных планов. Отложим от полюса плана ускорений pw отрезок pwa1, изображающий ускорение точки A кривошипа 1 (рис. 38). Длину этого отрезка примем равной 40 мм. Тогда масштаб плана ускорений 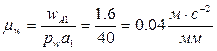 . Переведем в отрезки известные нам по величине ускорения:
. Переведем в отрезки известные нам по величине ускорения: 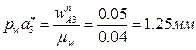 ,
, 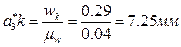 . Так как отрезок pwa*3 мал, пренебрежем его длиной, и будем считать, что точки pw и a*3 совпадают. Направление отрезка
. Так как отрезок pwa*3 мал, пренебрежем его длиной, и будем считать, что точки pw и a*3 совпадают. Направление отрезка 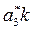 , изображающего ускорение Кориолиса, определим, повернув отрезок
, изображающего ускорение Кориолиса, определим, повернув отрезок 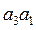 , изображающий относительную скорость
, изображающий относительную скорость 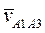 , (рис. 9) на 900 в направлении вращения кулисы 3. Замыкая векторный многоугольник направлениями ускорений
, (рис. 9) на 900 в направлении вращения кулисы 3. Замыкая векторный многоугольник направлениями ускорений 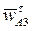 и
и 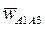 , в соответствии с уравнением (3) получим точку
, в соответствии с уравнением (3) получим точку 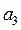 . Тогда отрезку
. Тогда отрезку 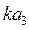 будет соответствовать относительное ускорение
будет соответствовать относительное ускорение 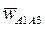 , а отрезку
, а отрезку 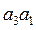 - тангенциальное ускорение
- тангенциальное ускорение 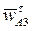 точки A, принадлежащей кулисе 3. Рассмотрим теперь движение суппорта 5 и кулисы 3. Согласно теореме о сложении ускорений имеем:
точки A, принадлежащей кулисе 3. Рассмотрим теперь движение суппорта 5 и кулисы 3. Согласно теореме о сложении ускорений имеем:
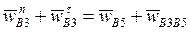 , (4)
, (4)
где 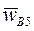 - ускорение суппорта 5,
- ускорение суппорта 5, 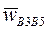 - ускорение точки B кулисы 3 относительно точки B суппорта 5. В данном случае
- ускорение точки B кулисы 3 относительно точки B суппорта 5. В данном случае 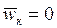 , так как переносное движение суппорта – поступательное. Нормальное ускорение
, так как переносное движение суппорта – поступательное. Нормальное ускорение 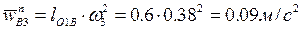 , отображающий это ускорение отрезок
, отображающий это ускорение отрезок 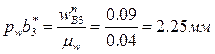 . Отрезок b*3b3, отображающий тангенциальное ускорение
. Отрезок b*3b3, отображающий тангенциальное ускорение 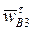 , найдем из соотношения:
, найдем из соотношения: 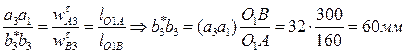 . Замыкая векторный многоугольник направлениями ускорений
. Замыкая векторный многоугольник направлениями ускорений 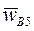 и
и 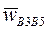 в соответствии с уравнением (4) получим точку b5 (рис. 10). Отрезок pwb5 отображает на плане ускорение суппорта 5. Длина этого отрезка – 55 мм, следовательно
в соответствии с уравнением (4) получим точку b5 (рис. 10). Отрезок pwb5 отображает на плане ускорение суппорта 5. Длина этого отрезка – 55 мм, следовательно 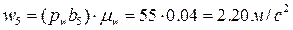 .
.
Таким образом, ускорение суппорта в положении механизма, изображенном на рис. 36, равно 2.20 м/c2 и направлено в ту же сторону, что и вектор скорости суппорта. Это означает, что в данный момент времени суппорт ускоряется. Планы скоростей и ускорений, изображенные на рис. 37 и рис. 38 соответственно, дают полную информацию о скоростях и ускорениях звеньев механизма в заданном на рис. 8 положении.
СИЛОВОЙ АНАЛИЗ
5.1.Определение неизвестных сил методом векторных планов
Найдем силы реакций в кинематических парах и движущий момент, приложенный к кривошипу 1, для положения механизма, изображенного на рис. 39. Значение силы резания P и параметры звеньев даны в таблице 3.
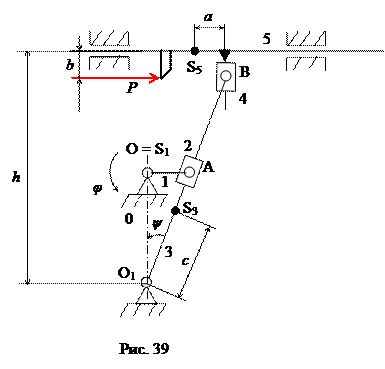 |
Таблица 3
| P, кН | h, м | a, м | b, м | c, м | m1, кг | m3, кг | m5, кг | J3, кг∙м2 |
| 1.2 | 0.70 | 0.10 | 0.10 | 0.25 | 5 | 10 | 12 | 0.3 |
На кинематической схеме буквой S с указанием номера звена обозначены центры масс соответствующих звеньев. Массами ползушек 2 и 4, а также силами трения в кинематических парах пренебрегаем.
Рассмотрим выходную группу звеньев 5-4. Выделим суппорт 5, обозначая все действующие на него силы (рис. 40).
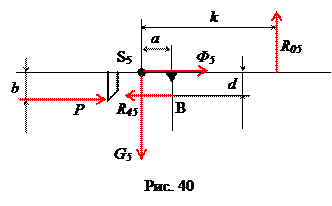 |
Сила инерции суппорта Ф5 приложена в его центре масс и направлена в сторону, противоположную ускорению wB5 (см. план ускорений на рис. 38). Равнодействующая сил тяжести суппорта G5 также приложена в центре масс и направлена вертикально вниз. Сила реакции R45 со стороны ползушки 4 приложена в точке B, так как ползушки имеют малые линейные размеры, и направлена под прямым углом к поверхности, вдоль которой перемещается ползушка 4. Равнодействующая R05 сил реакции стойки направлена под прямым углом к поверхности, вдоль которой перемещается суппорт, но плечо k этой силы относительно центра масс суппорта неизвестно. Проанализировав характер нагрузки на суппорт 5, заключаем, что необходимо определить три неизвестные величины: модули сил реакций R45, R05 и расстояние k. Для этого нам необходимо составить и решить три независимых уравнения кинетостатики звена. Уравнение сил в горизонтальном направлении имеет вид (силы, направленные вправо, учитываются со знаком «+»):
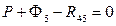 ,
,
откуда 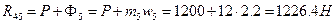 . Уравнение сил в вертикальном направлении (силы, направленные вверх, учитываются со знаком «+»):
. Уравнение сил в вертикальном направлении (силы, направленные вверх, учитываются со знаком «+»):
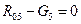 ,
,
откуда 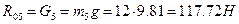 . Уравнение моментов относительно центра масс S5 суппорта (моменты сил, действующие против часовой стрелки, учитываются со знаком «+»):
. Уравнение моментов относительно центра масс S5 суппорта (моменты сил, действующие против часовой стрелки, учитываются со знаком «+»):
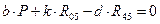 ,
,
откуда 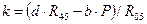 . Плечо d, согласно рис. 11, найдем из соотношения
. Плечо d, согласно рис. 11, найдем из соотношения
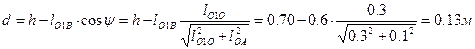 .
.
Соответственно, 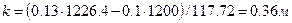 .
.
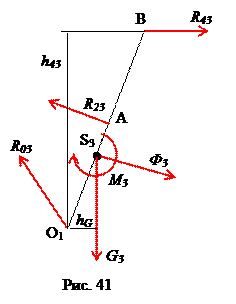
Теперь перейдем к группе звеньев 2-3. Выделим кулису 3, обозначая все действующие на нее силы (рис. 41).
Сила тяжести кулисы 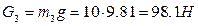 , направлена вертикально вниз. Сила инерции
, направлена вертикально вниз. Сила инерции 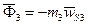 , где
, где 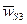 - ускорение центра масс S3 кулисы. Согласно плану ускорений (рис. 38), отрезок
- ускорение центра масс S3 кулисы. Согласно плану ускорений (рис. 38), отрезок 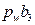 , изображающий полное ускорение точки B кулисы, равен 58 мм. Значение ускорения этой точки определится как произведение длины изображающего отрезка на масштаб плана ускорений:
, изображающий полное ускорение точки B кулисы, равен 58 мм. Значение ускорения этой точки определится как произведение длины изображающего отрезка на масштаб плана ускорений: 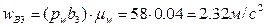 . Тогда ускорение центра масс S3 найдем из пропорции
. Тогда ускорение центра масс S3 найдем из пропорции
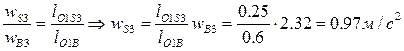 .
.
Абсолютная величина силы инерции кулисы 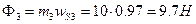 , направление – в сторону, противоположную ускорению центра масс. Момент сил инерции собственного вращения кулисы по абсолютной величине
, направление – в сторону, противоположную ускорению центра масс. Момент сил инерции собственного вращения кулисы по абсолютной величине 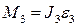 , где
, где 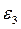 - угловое ускорение кулисы, которое найдем по формуле
- угловое ускорение кулисы, которое найдем по формуле
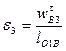 .
.
Из плана ускорений имеем 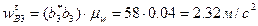 ,
, 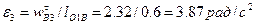 . Тогда
. Тогда 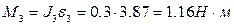 , направление момента сил инерции кулисы – в сторону, противоположную угловому ускорению (рис. 13). Сила реакции R43 со стороны ползушки 4 равна по модулю реакции R45 и направлена в противоположную сторону. Реакция R23 со стороны ползушки 2 направлена перпендикулярно перемещению ползушки 2, но неизвестен ее модуль. Реакция R03 со стороны стойки неизвестна ни по модулю, ни по направлению (на рис. 41 направление этой реакции указано произвольно).
, направление момента сил инерции кулисы – в сторону, противоположную угловому ускорению (рис. 13). Сила реакции R43 со стороны ползушки 4 равна по модулю реакции R45 и направлена в противоположную сторону. Реакция R23 со стороны ползушки 2 направлена перпендикулярно перемещению ползушки 2, но неизвестен ее модуль. Реакция R03 со стороны стойки неизвестна ни по модулю, ни по направлению (на рис. 41 направление этой реакции указано произвольно).
Величину реакции R23 определим из уравнения моментов относительно точки O1:
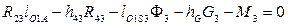 ,
,
откуда 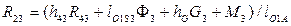 . Плечо силы R43
. Плечо силы R43 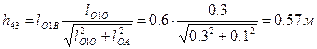 , плечо силы тяжести
, плечо силы тяжести 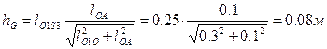 . Следовательно,
. Следовательно, 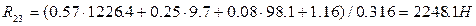 .
.
Реакцию R03 определим путем построения плана сил. Векторное уравнение сил имеет вид
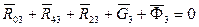 .
.
Пусть реакция R43 отображается на плане отрезком длины 50 мм. Тогда масштаб плана сил 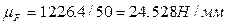 . Отрезок, изображающий реакцию R23:
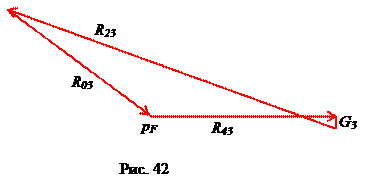
. Отрезок, изображающий реакцию R23: 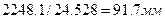 ; отрезки, изображающие силы G3 и Ф3 равны 4 мм и 0.4 мм соответственно. Ввиду малости отрезка, изображающего силу Ф3, пренебрежем в расчете этой силой. План сил, построенный в принятом масштабе, представлен на рис. 42.
; отрезки, изображающие силы G3 и Ф3 равны 4 мм и 0.4 мм соответственно. Ввиду малости отрезка, изображающего силу Ф3, пренебрежем в расчете этой силой. План сил, построенный в принятом масштабе, представлен на рис. 42.
Отрезок, изображающий реакцию R03, равен 47 мм, следовательно, 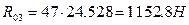 .
.
Рассмотрим начальную группу звеньев «стойка – кривошип». Выделим кривошип 1, обозначая все действующие на него силы (рис. 15).
 | |||
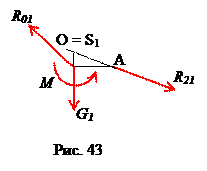 |
На кривошип действует сила тяжести 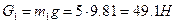 ; реакция со стороны ползушки 2, равная по модулю R23 и направленная в противоположную сторону; реакция со стороны стойки R01, не известная ни по модулю, ни по направлению (на рис. 15 эта реакция обозначена произвольно) и движущий момент M, не известный по величине.
; реакция со стороны ползушки 2, равная по модулю R23 и направленная в противоположную сторону; реакция со стороны стойки R01, не известная ни по модулю, ни по направлению (на рис. 15 эта реакция обозначена произвольно) и движущий момент M, не известный по величине.
Движущий момент M найдем из уравнения моментов относительно точки O:
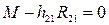 ,
,
где 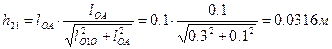 - плечо силы R21 относительно точки O.
- плечо силы R21 относительно точки O.
Получаем 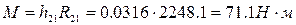 .
.
Реакцию R01 определим, построив план сил. Векторное уравнение сил, действующих на кривошип 1, имеет вид
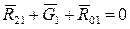 .
.
План сил в масштабе 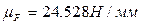 представлен на рис. 44.
представлен на рис. 44.

Отрезок, изображающий на плане реакцию R01, равен 92 мм, следовательно 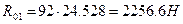 .
.
