Приближенные методы решения задач теплопроводности
Приближенные методы решения задач чаще всего применяются, когда точные аналитические методы расчета затруднительны.
Численный метод.Аналитические решения, полученные путем непосредственного интегрирования дифференциальных уравнений, дают возможность вычислить температуру в любой точке данной системы. В основу численного метода положено уравнение в форме конечных разностей, с помощью которого вычисляем температуру в некоторых заранее выбранных точках.
 Из численных методов решения задач теплопроводности наиболее часто используется метод конечных разностей. Сущность метода заключается в том, что в дифференциальном уравнении производные искомой функции заменяются приближенными соотношениями между конечными разностями в отдельных узловых точках температурного поля. В результате такой замены получается уравнение в конечных разностях, решение которого сводится к выполнению простых алгебраических операций.
Из численных методов решения задач теплопроводности наиболее часто используется метод конечных разностей. Сущность метода заключается в том, что в дифференциальном уравнении производные искомой функции заменяются приближенными соотношениями между конечными разностями в отдельных узловых точках температурного поля. В результате такой замены получается уравнение в конечных разностях, решение которого сводится к выполнению простых алгебраических операций.
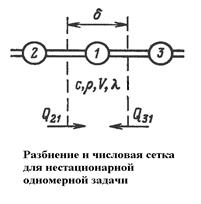
Для получения расчетных формул при численном интегрировании в настоящее время широко пользуются методом тепловых балансов. Сущность метода состоит в том, что система разбивается на элементарно малые объемы. Предполагается, что свойства каждого объема сосредоточены в центре каждого объема. Передача теплоты между узловыми точками осуществляется через условные теплопроводящие стержни.
Уравнение по определению температуры в искомой точке
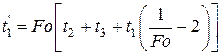
является основой численного метода расчета нестационарной теплопроводности. Для расчета температуры 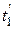 необходимо выбрать определенное значение Fo. Для одномерной задачи выбор ограничен условием устойчивости
необходимо выбрать определенное значение Fo. Для одномерной задачи выбор ограничен условием устойчивости 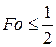 . При этом обеспечивается устойчивость уравнения. Если нарушается это условие, то изменение температуры в процессе расчета приобретает беспорядочный скачкообразный характер и расчет перестает быть верным. При выборе промежутков
. При этом обеспечивается устойчивость уравнения. Если нарушается это условие, то изменение температуры в процессе расчета приобретает беспорядочный скачкообразный характер и расчет перестает быть верным. При выборе промежутков 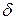 и
и 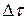 необходимо, чтобы условие устойчивости выполнялось. Если выбрать
необходимо, чтобы условие устойчивости выполнялось. Если выбрать 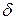 и
и 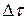 из условия
из условия 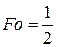 , то
, то 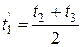 .
.
При 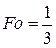
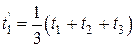 , при
, при 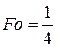
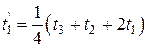 .
.
Следовательно, в результате уменьшения Fo увеличивается число вычислений и густота сетки, однако при этом повышается точность вычислений.
Вопросы к теме 3.
1. Какие процессы теплопроводности относятся к нестационарным?
2. Дать аналитическое описание процесса нестационарной теплопроводности.
3. Какие безразмерные переменные характеризуют нестационарный процесс теплопроводности?
4. Какие тела относятся к термически тонким и термически массивным телам. Проанализировать характер изменения температуры в телах в зависимости от численного значения числа Ві.
5. Как зависит процесс нагрева (охлаждения) от формы и размеров тела?
6. Какие стадии процесса нагрева (охлаждения) знаете?
7. Что такое темп охлаждения в регулярном режиме и от чего он зависит?
8. Сформулируйте первую и вторую теорему Кондратьева.
9. Какие методы решения задач теплопроводности знаете. В чем состоит сущность каждого из них?
