Методы решения краевой задачи в теории теплопроводности
Все методы решения краевой задачи теории теплопроводности можно разделить на две большие группы. К первой группе относят методы, использующие современные средства математического анализа, вычислительной математики
и вычислительной техники, поэтому их называют теоретическими методами. Во вторую группу включены методы, при использовании которых, температурное поле находят в результате проведения эксперимента. Поэтому их называют экспериментальными методами.
Экспериментальные методы делятся на методы теории подобия и методы аналогий. По методу теории подобия температурное поле находят экспериментально на модели, в которой реализуется процесс той же физической природы, что и в объекте моделирования. По методу аналогий исследование процесса теплопроводности заменяется исследованием процесса другой физической природы, который протекает аналогично процессу теплопроводности. Эта аналогия проявляется в одинаковых по форме записи дифференциальных уравнениях переноса, относящихся к разным физическим явлениям.
Теоретические методы можно подразделить на аналитические, численные, численно-аналитические методы.
При использовании аналитических методов решение получают в виде конечной формулы или бесконечного ряда. Различают точные аналитические методы (метод разделения переменных или метод Фурье, метод интегральных преобразований, метод конформных отображений и др.) и приближенные аналитические методы (различные формы вариационных методов, метод подстановок и др.). Точные аналитические методы можно применять только к линейным задачам теории теплопроводности.
При использовании численных методов решение задачи получают в виде набора значений температур в дискретных точках пространства в дискретные моменты времени. В настоящее время для методами решения задач теплообмена наиболее часто используют метод сеток и метод конечных элементов.
Методы, которые используют аналитические решения для получения значений температур в дискретных точках пространства в дискретные моменты времени, называются численно-аналитическими (метод граничных элементов, метод R-функций, метод дискретного удовлетворения краевых условий и др.). В результате решения задачи
нестационарной теплопроводности находят температурное поле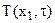 
, изменяющееся в пространстве и во времени. Точные аналитические решения дифференциального уравнения теплопроводности для тел простейшей формы с граничными условиями I, II и III родов приведены в методических указаниях "Нестационарная теплопроводность" №1684. Для удобства инженерных расчетов аналитическое решение при ГУ III рода представлено
в виде графиков – номограмм, которые для тел простейшей формы также приведены в той же методичке №1684. Поэтому далее рассмотрим постановку задачи и алгоритм определения температурного поля с помощью номограмм.
Стационарная теплопроводность плоской стенки при граничных условиях
Первого рода.
Бесконечно большая плоская стенка толщиной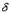 
теплопроводностью 
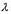передает тепло при постоянных температурах на границе 
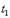и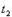 
.
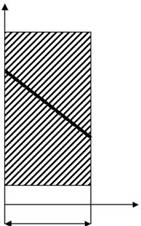
Определить характер изменения температуры по толщине стенки и тепловой поток через стенку.
При рассматриваемых условиях теплота может распространяться только вдоль оси x, и температурное поле будет одномерным.
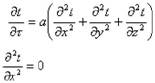
| (1) | |
| Проинтегрировав (1) дважды, найдем: | (2) |
| ниже - x = 0: t = t1 | |
| : t = t2 |
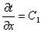
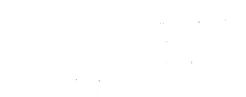
- уравнение температурного поля.
Определим плотность теплового потока через плоскую стенку. В соответствии с законом Фурье с учетом равенства
(2) можно записать
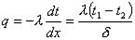
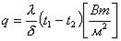
то же, только иначе
Плотность теплового потока проходящего через плоскую стенку прямо пропорциональна разности температур ее
поверхностей и обратно пропорциональна термическому сопротивлению.
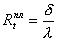
- термическое сопротивление плоской стенки.
Если стенка многослойная, то термическое сопротивление ее будет складываться из термических сопротивлений каждого слоя и сопротивлений контактов.