Необходимый признак сходимости числовых рядов.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Понятие дифференциального уравнения.
Дифференциальным уравнением называют уравнение, которое связывает
y - неизвестную функцию
x - независимую переменную
и - различные производные от функции y по переменной x :
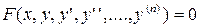 .
.
Порядком дифференциального уравнения называют наибольший порядок производной, которая входит в данное уравнение.
Линейные дифференциальные уравнения I-го порядка.
Уравнение вида
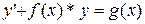 (1)
(1)
называется линейным уравнением I-го порядка, где f(x) и g(x) - функции от независимой переменной x.
Если функция g(x) = 0, то линейное уравнение называется линейным однородным уравнением.
Если функция g(x) ¹ 0 , то уравнение называется линейным неоднородным уравнением I-го порядка.
Решение данного вида уравнений ищется в виде произведений двух функций u и v:
y = u* v ; u = u(x) и v = v(x) .
подставим в (1) y = u'* v + u* v' получим:
u'* v + u* v' + f(x)* u*v = g(x) ,
u'* v + u* (v' + f(x)*v) = g(x) (*)
Ищем неизвестную функцию v из условия: содержимое скобки равно нулю
v' + f(x)*v = 0 ; 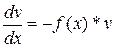 ;
; 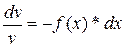 ;
;
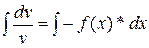 ;
; 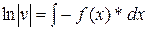 ;
; 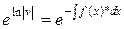 ;
;
Учитывая операцию потенцирования 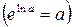 получаем
получаем 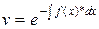 .
.
Для того, чтобы найти неизвестную функцию u , возвратимся к выражению (*):
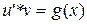 ;
; 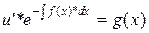 ;
; 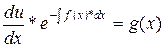 ;
;
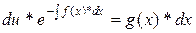 ;
; 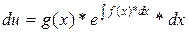 ;
;
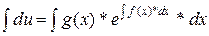 ;
;
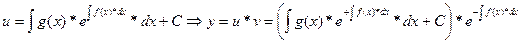 .
.
Линейные однородные дифференциальные уравнения II-го порядка с постоянными коэффициентами.
Уравнение вида 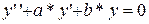 , где
, где 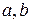 - числа, называется линейным однородным дифференциальным уравнением с постоянными коэффициентами.
- числа, называется линейным однородным дифференциальным уравнением с постоянными коэффициентами.
Чтобы найти общее решение данного уравнения, составляют характеристическое уравнение, которое имеет следующий вид
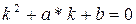
1. 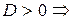 2 различных действительных корня
2 различных действительных корня 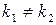 . Общее решение дифференциального уравнения имеет следующий вид:
. Общее решение дифференциального уравнения имеет следующий вид:
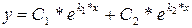 .
.
2. 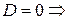
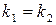 . Общее решение
. Общее решение 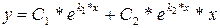 .
.
3. 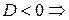 корни комплексные
корни комплексные 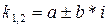 .
. 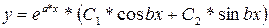 .
.
Линейные неоднородные дифференциальные уравнения II-го порядка с постоянными коэффициентами.
Это уравнение вида
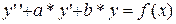 , где
, где
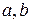 - числа,
- числа,
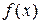 - функция от переменной
- функция от переменной 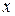 .
.
Решение данного уравнения будем искать в следующем виде
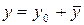 , где
, где
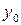 - общее решение соответствующего однородного уравнения
- общее решение соответствующего однородного уравнения
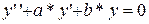 .
.
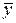 - частное решение неоднородного уравнения.
- частное решение неоднородного уравнения.
Для нахождения частного решения 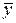 будем использовать следующую таблицу:
будем использовать следующую таблицу:
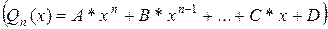
Вид 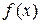 | Корни характеристического уравнения | Вид решения 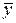 |
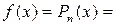 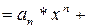 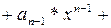 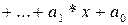 | 1) 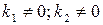 . 2) . 2) 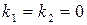 . 3) . 3) 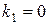 или или 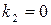 . . | 1) 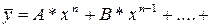 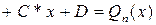 . 2) . 2) 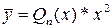 . 3) . 3) 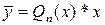 . . |
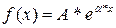 | 1) 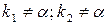 . 2) . 2) 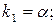 или или 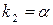 . . | 1) 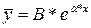 2) 2) 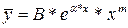  - кратность - кратность  для характеристического уравнения (сколько раз является корнем). для характеристического уравнения (сколько раз является корнем). |
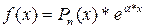 | 1) 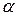 - корень; 2) - корень; 2) 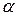 - не является корнем. - не является корнем. | 1) 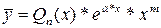 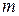 - кратность - кратность 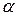 2) 2) 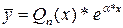 |
РЯДЫ.
Пусть дана последовательность чисел 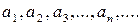
Числовым рядомназывается выражение вида
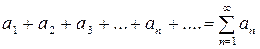 (1).
(1).
Числа 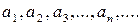 - члены ряда.
- члены ряда.
Выражение 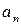 - формула n-го члена.
- формула n-го члена.
Необходимый признак сходимости числовых рядов.
Теорема:Если ряд 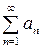 сходится, то предел общего члена
сходится, то предел общего члена 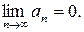
Достаточные признаки сходимости:
Теорема 1 (признак сравнения):Пусть даны 2 положительных ряда:
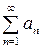 (1) и
(1) и
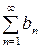 . (2)
. (2)
Если между членами этих рядов выполняется неравенство 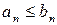 , то из сходимости ряда (2) будет следовать сходимость ряда (1) и из расходимости ряда (1) будет следовать расходимость ряда (2) .
, то из сходимости ряда (2) будет следовать сходимость ряда (1) и из расходимости ряда (1) будет следовать расходимость ряда (2) .
Теорема 2 (признак Даламбера):
Если для положительного ряда 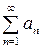 выполняется следующее условие
выполняется следующее условие 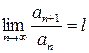 , то если l < 1 - ряд будет сходиться,
, то если l < 1 - ряд будет сходиться,
если l > 1 - ряд будет расходиться.
Теорема 3 (признак Коши):
Если для положительного ряда 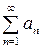 выполняется следующее условие
выполняется следующее условие 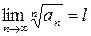 , то если l < 1 - ряд будет сходиться,
, то если l < 1 - ряд будет сходиться,
если l > 1 - ряд будет расходиться.
Теорема (признак Лейбница) Если в знакочередующемся ряде все члены таковы, что
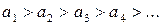 и
и 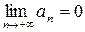 , то числовой ряд сходится.
, то числовой ряд сходится.
Степенные ряды.
Ряд вида 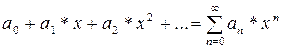 (1), где
(1), где
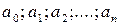 - числа, а
- числа, а
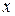 - переменная, называется степенным рядом.
- переменная, называется степенным рядом.
Теорема 2: Если для ряда (1) существует 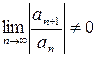 , то радиус сходимости степенного ряда
, то радиус сходимости степенного ряда 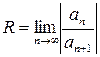 .
.
Разложения в ряд Маклорена некоторых элементарных функций (эти разложения следует запомнить):
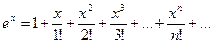 ,
, 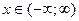 , (10.4)
, (10.4)
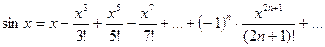 ,
, 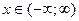 , (10.5)
, (10.5)
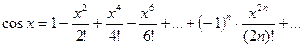 ,
, 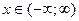 , (10.6)
, (10.6)
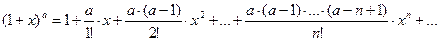 ,
,
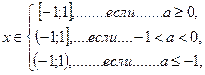 (10.7)
(10.7)
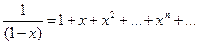 ,
, 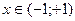 , (10.8)
, (10.8)
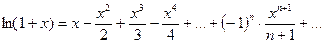 ,
, 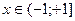 , (10.9)
, (10.9)
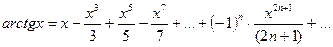 ,
, 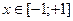 , (10.10)
, (10.10)
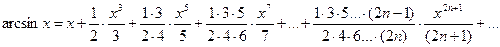 , (10.11)
, (10.11)
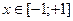 , (10.12)
, (10.12)
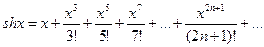 ,
, 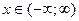 , (10.13)
, (10.13)
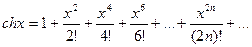 ,
, 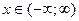 . (10.14)
. (10.14)
