Второй способ проверки закона
Описание установки (см. рис.7 )
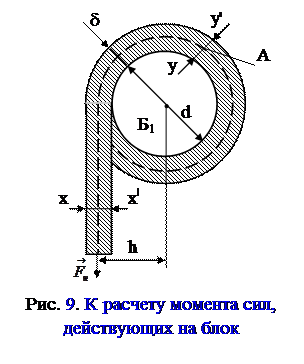 На вертикальной оси ОО’ прибора укреплен блок Б1 диаметром d, который при помощи намотанной на него нити и груза m можно привести во вращение. На этой же оси укреплена крестовина, состоящая из горизонтального стержня с массивными грузами 1 и 2 равной массы (m1 = m2). Крестовина и блок Б1 вращаются как единое целое. Второй блок Б2, ось которого горизонтальна, служит для изменения направления нити. Установка снабжена тормозом Т и шкалой для измерения пути, пройденного грузом m. Вид сверху на блок Б1 с намотанной на него нитью толщиной d показан на рис. 9.
На вертикальной оси ОО’ прибора укреплен блок Б1 диаметром d, который при помощи намотанной на него нити и груза m можно привести во вращение. На этой же оси укреплена крестовина, состоящая из горизонтального стержня с массивными грузами 1 и 2 равной массы (m1 = m2). Крестовина и блок Б1 вращаются как единое целое. Второй блок Б2, ось которого горизонтальна, служит для изменения направления нити. Установка снабжена тормозом Т и шкалой для измерения пути, пройденного грузом m. Вид сверху на блок Б1 с намотанной на него нитью толщиной d показан на рис. 9.
Описание эксперимента (рис. 7)
При освобождении от тормоза груз m опускается равноускоренно из положения О в положение 1, проходя путь Н1. Соответственно крестовина вращается равноускоренно. Это движение длится t1 c. Затем груз m резко меняет направление скорости на противоположное и поднимается равнозамедленно из положения 1 в положение 2, пройдя путь Н2 за время t2 с. Соответственно крестовина вращается равнозамедленно, но в отличие от груза m не меняет направления своего движения. В положении О и 2 скорость груза (а также и крестовины) равна 0. В положении 1 величина скорости груза не имеет определенного значения: при приближении к пункту 1 она больше, чем при удалении от него. Это является следствием частичной потери кинетической энергии. Экспериментальное определение Н1, t1 и Н2, t2 достаточно для независимых друг от друга расчетов I, M и i, что позволяет проверить основной закон динамики для вращательного движения.
Расчет момента инерции крестовины.
Момент инерции крестовины относительно оси ОО’ не зависит от состояния ее движения и может быть рассчитан по формуле
I=Iгр+Iст
где Iгр – момент инерции грузов m1 и m2, а Iст – момент инерции стержня, на котором они закреплены. Поскольку m1 = m2, Iгр=2m1R2, где R – расстояние от оси ОО’ до центра груза, одинаковое для обоих грузов.
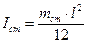 , где mст - масса стержня. Таким образом
, где mст - масса стержня. Таким образом
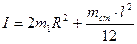 (1)
(1)
Учет моментов сил, действующих на крестовину.
На каждом участке движения (ускоренном или замедленном) на крестовину действуют моменты двух сил: силы натяжения нити Fн и силы трения в опорных деталях конструкции. Обозначим эти моменты соответственно М и m. Для расчета М надо знать величину силы Fн и плечо h этой силы относительно оси вращения ОО’. Силу Fн можно оценить, применив второй закон Ньютона к движению груза m.
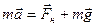
В наших опытах ускорение грузa а<<g. Поэтому можно принять Fн=mg
Сложнее оценить плечо h. Дело в том, что Fн не является сосредоточенной силой, а распределена по поперечному сечению нити. Учитывая спиралевидный переплет волокон, из которых состоит нить, следует считать это распределение равномерным. Тогда распределенную силу Fн можно заменить сосредоточенной, действующей вдоль осевой линии нити (на рис.9 осевая линия обозначена пунктиром). Для сосредоточенной силы получим
h=0.5(d+d)
где d - диаметр блока Б1, а d – диаметр нити. Таким образом
M= Fн×0.5(d+d)=mg×0.5(d+d)= mgr (2)
Величина тормозящего момента m практически одинакова на всех участках движения. Это позволяет провести опыт так, чтобы исключить из рассмотрения момент m. Для участка ускоренного движения крестовины основной закон запишется в виде
I×i1=M-m
Для участка замедленного движения будем иметь
I×i2=M+m
где i1 и i2 - угловые ускорения на первом и втором участке. Складывая два уравнения, получим I(i1+ i2)=2M или
M= I×i (3)
где i=0.5(i1+ i2)
Уравнение (3) подлежит экспериментальной проверке.
Расчет угловых ускорений
Угловое ускорение i связано с ускорением a поступательного движения груза m. Поскольку v0=v2=0, то из формулы пути равнопеременного движения получим 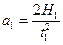 и
и 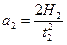 на участке ускоренного и замедленного движения соответственно.
на участке ускоренного и замедленного движения соответственно.
Все точки нити, расположенные в сечении xx’ (см. рис. 9), движущемся поступательно, имеют одинаковое ускорение, равное ускорению груза. Но точки нити, расположенные в сечении yy’, имеют разные тангенциальные ускорения, поскольку этот участок нити вращается вместе с блоком Б1. Ускорение груза m совпадает с величиной тангенциального ускорения точки, лежащей на осевой линии нити (точка А на рис. 9). Радиус вращения точки А rA=r=0.5(d+d). Угловые ускорения i блока Б1 и iA точки А одинаковы вследствие отсутствия проскальзывания нити. Пользуясь связью между угловым и тангенциальным ускорением точки А находим.

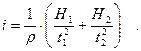 (4)
(4)
Порядок выполнения работы.
1. Внимательно прочтите раздел «Описание эксперимента».
2. Измерьте расстояние Н1 от нулевого деления шкалы до нижнего положения груза m при полностью раскрученной нити. Отсчет сделайте по верхнему краю груза m.
3. Установите грузы m1 и m2 на одинаковом расстоянии R от оси вращения ОО’, указанном преподавателем.
4. Расположите верхний край груза m против деления ¢¢0¢¢ на шкале и зафиксируйте это положение тормозом. Установка готова к выполнению эксперимента.
5. Определите опытным путем отрезки времени t1 и t2. Для этого воспользуйтесь двумя секундомерами. Освободите тормоз и одновременно включите один из секундомеров. Когда груз опустится в крайнее нижнее положение, остановите работающий секундомер (отчет t1) и одновременно включите другой. Второй секундомер остановите, когда груз поднимется в положение 2, показанное на рис. 7 (отчет t2) . Зафиксируйте груз в этом положении, включив тормоз. Сделайте отчет h по верхнему краю груза.
Если Вы работаете с одним секундомером, то отчеты t1 и t2 придется делать при двух разных запусках груза m.
6. Повторите указанные измерения 5 раз. Результаты занесите в табл. 1. Определите приближенные (средние) значения 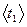 ,
, 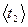 ,
, 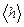 а также абсолютные погрешности Dt1, Dt2, Dh по методу Стьюдента. В эту же таблицу запишите измеренное в п. 2 значение Н1 и выбранную величину R. Поскольку случайный разброс практически равен нулю,
а также абсолютные погрешности Dt1, Dt2, Dh по методу Стьюдента. В эту же таблицу запишите измеренное в п. 2 значение Н1 и выбранную величину R. Поскольку случайный разброс практически равен нулю, 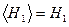 , DH1=1×10-2 м.
, DH1=1×10-2 м. 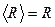 , DR=5×10-3 м
, DR=5×10-3 м
7. Запишите в таблицу 2 параметры экспериментальной установки, приближенные значения которые указаны на самом приборе.
8. По формулам (1), (2) и (4) рассчитайте приближенные значения 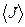 ,
, 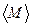 ,
, 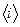 , подставив в них приближенные значения соответствующих величин, взятые из табл. 1 и 2. Определите приближенные значения произведения
, подставив в них приближенные значения соответствующих величин, взятые из табл. 1 и 2. Определите приближенные значения произведения 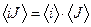 . Заполните табл. 3. Если
. Заполните табл. 3. Если 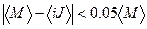 , то формулу (3) можно считать подтвержденной.
, то формулу (3) можно считать подтвержденной.
9. Более строгим подтверждением формулы (3) является проверка доверительных интервалов величин М и (J×i) на их перекрытие, наличие которого будет служить свидетельством справедливости проверяемого закона. Для этого надо рассчитать абсолютные погрешности DM и D(J×i) по формулам
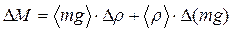 ,
,
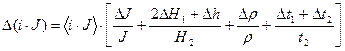
и записать доверительные интервалы в виде
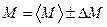 и
и 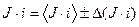
Для наглядности эти интервалы рекомендуется изобразить на числовой оси.

Таблица 1.
Результаты измерений
| № п.п. | t1, c | t2, c | h, м | H1, м | R, м |
 | |||||
| D | 1×10-2 | 5×10-3 |
Таблица 2.
Параметры установки
| m1=m2,кг | l, м | mст, кг | m, кг | r, м | |
 | 431×10-3 | 510×10-3 | 111×10-3 | 152×10-3 | 10.4×10-3 |
| D | 1×10-3 | 5×10-3 | 1×10-3 | 1×10-3 | 0.1×10-3 |
Таблица 3.
Результаты вычислений
| H2, м | i, c-2 | I, кг×м2 | I×i | M, Н×м | |
 | |||||
| D |
Контрольные вопросы
1. Что называется угловой скоростью и угловым ускорением? Их направление и единицы измерения.
2. Как в данной работе определялось угловое ускорение стержня с грузами?
3. Что называется моментом инерции тела? Единицы измерения момента инерции в системе СИ. От чего зависит величина момента инерции?
4. Где должна проходить ось вращения, чтобы момент инерции тела был наименьшим? Как рассчитать момент инерции тела относительно оси, не проходящей через его центр масс? Как рассчитать момент инерции тела с грузами в данной работе?
5. Что называется моментом силы относительно точки и относительно оси? Единицы измерения момента силы.
6. В чем состоит основной закон динамики для вращательного движения? Как этот закон проверялся в данной работе?
Литература
1. Савельев И. В. Курс физики. В 3 тт. СПб.: Издательство «Лань», 2008.
2. Детлаф А. А. , Яворский Б. М. Курс физики: Учебн. пособие для втузов. - М.: Высшая школа, 1989. - 607 с. - предм. указ.: с. 588-603.
3. Трофимова Т.И. Курс физики: учеб. пособие для вузов //Т.И. Трофимова. – 16-у изд., стер. – М.: Издательский цунтр «Академия», 2008. – 560с.
4. Биргер Б.Н. Приближения при вычислениях и измерениях. : Метод. указания к решению задач и выполнению лабораторных работ по физике - Иваново, ИХТИ, 1989 г. - 28с.
5. Бутман М.Ф., Кудин Л.С. Обработка и представление результатов измерений. Методические указания к лабораторному практикуму. - Иваново 2005. 36с.
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ
ФИЗИЧЕСКОГО МАЯТНИКА
Цель работы: ознакомление с физическим маятником и определение его момента инерции относительно оси вращения. Изучение зависимости величины момента инерции маятника от пространственного распределения массы.
Приборы и принадлежности: физический маятник с кронштейном для его подвеса, металлическая призма для определения положения центра тяжести маятника, секундомер.
Теоретическое введение.
 |
Физическим маятником (рис.1) называется любое твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси (О), не проходящей через центр его тяжести (С). Точка подвеса маятника является центром вращения.
Рис.1. Физический маятник
При отклонении маятника от положения равновесия на угол a возникает вращающий момент, созданный силой тяжести:
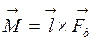
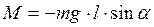 ,
,
где l – расстояние между точкой подвеса и центром тяжести маятника (знак минус обусловлен тем, что момент силы М имеет такое направление, что стремится вернуть маятник к положению равновесия, т.е. уменьшить угол a).
Для малых углов отклонения 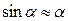 , тогда
, тогда
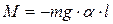 (1)
(1)
С другой стороны момент возвращающей силы можно записать в виде:
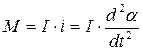 (2)
(2)
I – момент инерции маятника
i – угловое ускорение.
Из (1) и (2) можно получить:
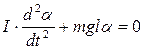
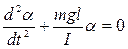 .
.
Обозначая 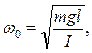 (3)
(3)
получим 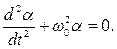 (4)
(4)
Уравнение (4) – линейное дифференциальное уравнение 2-го порядка. Его решением является выражение 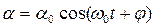 .
.
С учетом уравнения (3) период малых колебаний физического маятника можно записать как:
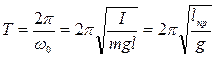 , (5)
, (5)
где 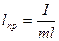 - приведенная длина физического маятника
- приведенная длина физического маятника
Из формулы (5) можно выразить момент инерции физического маятника относительно оси вращения
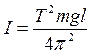 (6)
(6)
Находя путем измерений m, l и T, можно по формуле (6) вычислить момент инерции физического маятника относительно заданной оси вращения.
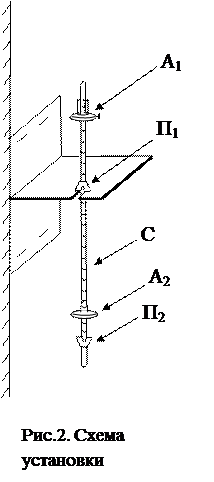
В данной работе используется физический маятник (рис.2), представляющий собой стальной стержень, на котором закреплены две массивные стальные чечевицы (А1 и А2) и опорные призмы для подвеса (П1 и П2). Момент инерции такого маятника будет складываться из моментов инерции стержня, чечевиц и призм:
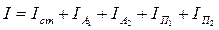 .
.
Момент инерции стержня можно рассчитать с помощью теоремы Штейнера:
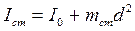 ,
,
где I0 - момент инерции стержня относительно оси, проходящей через центр тяжести.
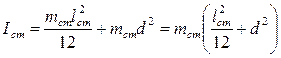 (7)
(7)
mст– масса стержня,
lст – длина стержня,
d – расстояние от центра тяжести стержня до точки подвеса.
Моменты инерции чечевиц и призм можно приближенно рассчитать как для точечных масс. Тогда момент инерции маятника запишется в виде:
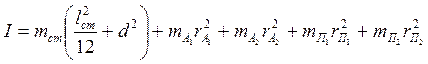 , (8)
, (8)
где 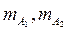 - массы чечевиц А1 и А2,
- массы чечевиц А1 и А2,
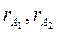 - расстояния от оси вращения (точки подвеса) до чечевиц А1 и А2 соответственно,
- расстояния от оси вращения (точки подвеса) до чечевиц А1 и А2 соответственно,
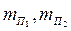 - массы призм П1 и П1,
- массы призм П1 и П1,
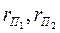 - расстояния от оси вращения до призм П1 и П2 соответственно.
- расстояния от оси вращения до призм П1 и П2 соответственно.
Т.к. по условиям выполнения работы перемещается лишь одна чечевица А1, то изменяться будет лишь момент инерции 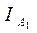 и
и
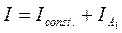
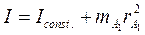 (9)
(9)
Описание установки.
Применяемый в данной работе физический маятник (рис.2) представляет собой стальной стержень (С), на котором закреплены две массивные стальные чечевицы (А1 и А2) и опорные призмы для подвеса (П1 и П2). Маятник подвешивается на кронштейне.
Посредством перемещения одной из чечевиц можно изменить момент инерции маятника относительно точки подвеса (оси вращения).
Центр тяжести маятника определяется балансированием маятника на горизонтальном ребре специальной призмы (рис.3). На стержне маятника через 10 мм нанесены кольцевые нарезки, служащие для точного определения расстояния от центра тяжести до оси вращения без помощи линейки. Небольшим смещением чечевицы А1 вдоль стержня можно добиться, чтобы расстояние l от точки подвеса до центра тяжести равнялось целому числу сантиметров, отсчитываемому по шкале на стержне.
Порядок выполнения работы.
1. Определить положение центра тяжести маятника.
а) Снять маятник с кронштейна и установить его в горизонтальном положении на специальной призме П3 (рис.3) так, чтобы он находился в равновесии. Точное положение равновесия достигается небольшим передвижением чечевицы А1.

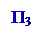
Рис.3. Уравновешивание маятника
б) По шкале на маятнике измерить l - расстояние от точки подвеса (ребро призмы П1) до центра тяжести маятника (верхнее ребро призмы П3).
в) По шкале маятника измерить расстояние 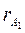 - от точки подвеса (ребро призмы П1) до верхней чечевицы А1.
- от точки подвеса (ребро призмы П1) до верхней чечевицы А1.
2. Определить период колебаний физического маятника.
а) Установить маятник призмой П1 на кронштейн (рис.2)
б) Определить время полных 50 - 100 колебаний маятника. Записать время t и число n колебаний маятника.
в) Определить период колебаний физического маятника по формуле:
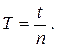 (10)
(10)
3. Снять маятник с кронштейна. Передвинуть чечевицу А1 на несколько сантиметров в новое положение и повторить опыт. Измерения должны быть выполнены не менее, чем для трех различных положений чечевицы А1 относительно точки подвеса.
4. По формуле (6) вычислить момент инерции физического маятника Iоп.
5. Вычислить относительную погрешность момента инерции для одного из рассмотренных случаев по формуле:
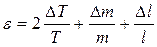 . (11)
. (11)
Величины DT и Dl определяются по классу точности приборов.
6. Найти абсолютную погрешность 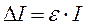 для каждого случая, принимая относительную погрешностьодинаковой для всех случаев.
для каждого случая, принимая относительную погрешностьодинаковой для всех случаев.
Записать в таблицу окончательный результат в виде
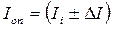
7. По формуле (8) вычислить момент инерции маятника Iтеор для каждого случая.
8. Сравнить полученные результаты Iоп и Iтеор, вычислив отношение:
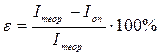 (12)
(12)
Сделать вывод о том, насколько велико расхождение полученных значений и каковы причины расхождений.
Таблица
Результаты измерений и вычислений
| № п/п | l, м | t, с | n | T, c | 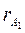 , м , м | 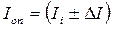 , кг м2 , кг м2 | Iтеор, кг м2 | 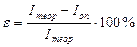 |
Контрольные вопросы.
1. Что такое физический маятник?
2. Что называется приведенной длиной физического маятника?
3. Какое колебание называется гармоническим?
4. Что такое период колебаний?
5. Выведите формулу для вычисления периода колебаний физического маятника.
6. Что такое момент инерции? В чем заключается аддитивность момента инерции?
7. Как рассчитать момент инерции тела относительно оси, не проходящей через центр его тяжести?
8. Получите формулу для вычисления момента инерции физического маятника.
Литература
1. Савельев И. В. Курс общей физики: Учебн. пособие для втузов: в 3 т. Т.1: Механика. Молекулярная физика. - 3-е изд., испр. - М.: Наука, 1986. – 432с.
2. Детлаф А. А. , Яворский Б. М. Курс физики: Учебн. пособие для втузов. - М.: Высшая школа, 1989. - 607 с. - предм. указ.: с. 588-603.
3. Лабораторный практикум по физике: Учеб. пособие для студентов втузов/ Б. Ф. Алексеев, К. А. Барсуков, И. А. Войцеховская и др.; Под ред. К. А. Барсукова и Ю. И. Уханова. – М.: Высш. школа,1988. – 351 с.: ил.
ISBN 5-06-001365-0
4.Майсова Н.Н. Практикум по курсу общей физики. – М.: Высшая школа, 1970
Определение ускорения свободного падения
с помощью оборотного маятника
Цель работы: познакомиться с оборотным маятником и определить с его помощью ускорение свободного падения.
Приборы и принадлежности: оборотный маятник, секундомер.
Теоретическое введение
Маятником называют твердое тело, способное под действием силы тяжести совершать колебания вокруг неподвижной точки или оси. Принято различать математический и физический маятники.
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена материальная точка (тело, размерами которого можно пренебречь). Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити. Период колебаний математического маятника равен:
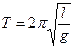 (1),
(1),
где l– длина маятника, g– ускорение свободного падения.
Физическим маятником называется твердое тело, укрепленное на неподвижной горизонтальной оси, не проходящей через его центр масс. Под действием силы тяжести физический маятник способен совершать колебания относительно этой оси. При малых колебаниях период колебаний физического маятника определяется формулой:
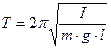 (2),
(2),
где I– момент инерции маятника относительно горизонтальной оси, проходящей через точку подвеса; m– масса маятника; l– расстояние между точкой подвеса и центром масс маятника.
Сопоставление формул (1) и (2) показывает, что математический маятник с длиной
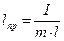 (3)
(3)
будет иметь такой же период колебаний, как и данный физический маятник. Величину (3) называют приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Этот период задается формулой:
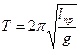 (4).
(4).
Точка О' на прямой, соединяющей точку подвеса О с центром масс C, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (рис. 1). Приведенная длина всегда больше l, поэтому точка подвеса и центр качания лежат по разные стороны от центра масс.
Можно показать, что при подвешивании маятника в центре качания О' приведенная длина маятника, а значит и его период колебаний, будут теми же, что и вначале (когда маятник был подвешен в точке О). Следовательно, точка подвеса О и центр качания О' обладают свойством взаимозаместимости: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.
На этом свойстве основано определение ускорения свободного падения с помощью так называемого оборотного маятника. Оборотным называют такой физический маятник, у которого имеются две параллельные друг другу, закрепленные вблизи его концов опорные призмы, за которые маятник можно поочередно подвешивать. Закрепленные на маятнике тяжелые грузы можно перемещать вдоль маятника. Перемещением грузов можно добиться того, чтобы при подвешивании маятника за любую из опорных призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно приведенной длине физического маятника lпр. Измерив период колебаний маятника и зная lпр , можно по формуле (4) найти ускорение
 |
свободного падения g.

Описание установки
Используемый в данной работе оборотный маятник изображен на рисунке 2. Маятник представляет собой стальной стержень С, снабженный двумя неподвижными опорными призмами П1 и П2. На стержне закреплены две массивные стальные чечевицы A1 и A2. Чечевицу A2 можно перемещать вдоль стержня и закреплять в различных положениях, определяемых расстоянием b от конца стержня. Маятник подвешивают на кронштейне К поочередно за каждую из призм П1 и П2. Перемещением чечевицы A2 добиваются того, чтобы при подвешивании на призмах П1 и П2 период колебаний маятника был одинаков. Тогда расстояние между опорными ребрами призм будет равно приведенной длине lпр.
Порядок выполнения работы
1. Закрепите чечевицу А2 на некотором расстоянии b от конца стержня.
2. Установите маятник на опорной призме П1. Приведите маятник в колебательное движение, отклонив его на небольшой угол (не более 10°) от вертикальной оси. Найдите период колебаний 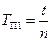 , трижды определив время t, за которое маятник совершает n колебаний (рекомендуем взять n = 10), и вычислив среднее арифметическое tср. Результаты измерений и вычислений занесите в таблицу 1.
, трижды определив время t, за которое маятник совершает n колебаний (рекомендуем взять n = 10), и вычислив среднее арифметическое tср. Результаты измерений и вычислений занесите в таблицу 1.
3. Установите маятник на опорной призме П2 и проведите измерения периода колебаний 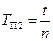 так же, как описано в пункте 2.
так же, как описано в пункте 2.
Опыты (1-3) рекомендуем провести при пяти–шести (k = 5¸6) положениях чечевицы А2, например, соответствующих расстояниям b1 = 2, b2 = 6, b3 = 10, b4 = 14, b5 = 18 см.
4. Постройте графики ТП1 = f1(b) и ТП2 = f2(b) зависимостей периода колебаний маятника от положения чечевицы А2, откладывая по оси абсцисс расстояние b, а по оси ординат периоды колебаний ТП1 и ТП2, измеренные при различных значениях b при двух положениях маятника (с опорой на призму П1 и на призму П2). Координата bx точки пересечения кривых ТП1 = f1(b) и ТП2 = f2(b) определяет такое положение чечевицы А2, при котором периоды ТП1 и ТП2 одинаковы: ТП1 = ТП2 = Т.
5. Уточните значение периода колебаний маятника Т при найденном положении bx чечевицы А2. Для этого закрепите чечевицу А2 в положении bx и, подвесив маятник сначала на призме П1, а потом на призме П2, по три раза измерьте соответствующие времена t1 и t2, за которые маятник совершает n колебаний (во всех опытах возьмите одно и то же значение n = 10). Вследствие погрешности определения расстояния bx величины ТП1 и ТП2, а следовательно и величины t1 и t2, могут отличаться друг от друга. Необходимое для вычисления периода колебаний 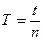 наиболее вероятное значение t времени n колебаний, а также абсолютную погрешность Δt величины t найдите методом Стьюдента, используя шесть измеренных значений t (трех величин t1 и трех величин t2). Результаты измерений и расчетов занесите в таблицу 2.
наиболее вероятное значение t времени n колебаний, а также абсолютную погрешность Δt величины t найдите методом Стьюдента, используя шесть измеренных значений t (трех величин t1 и трех величин t2). Результаты измерений и расчетов занесите в таблицу 2.
6. Определите приведенную длину маятника lпр, измерив расстояние между ребрами опорных призм (при измерении можно использовать нанесенные на стержень маятника сантиметровые метки).
7. Вычислите g по формуле: 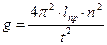 .
.
8. Вычислите относительную погрешность определения величины g по формуле:
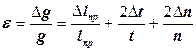 ,
,
при этом погрешность Δn определения числа колебаний можно принять равной нулю.
9. Найдите абсолютную погрешность:
Δg = ε·g .
10. Запишите окончательный результат:
g = (g ± Δg); ε = . . . .
Сравните этот результат с величиной ускорения свободного падения, приводимой в справочниках по физике: g = 9.80665 м/с2.
Таблица 1
Измерения периода колебаний оборотного маятника при опоре на призму П1 и на призму П2 при различных положениях b чечевицы А2
| b, см | № | Призма П1 | Призма П2 | ||||
| t, с | tср, с | T, с | t, с | tср, с | T, с | ||
| b1 | |||||||
| b2 | |||||||
| · · · | |||||||
| bk |
Таблица 2
Измерения периода колебаний оборотного маятника при положении чечевицы А2 , равном bx = . . . см
| lпр, м | n | П1 t1, с | П2 t2, с | t, с | Δt, с | 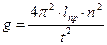 , м/с2 , м/с2 |
Контрольные вопросы
1. Что такое математический маятник? Что такое физический маятник?
2. Запишите формулы для периодов колебаний математического и физического маятников. Какие предположения использованы при выводе этих формул?
3. Что называется приведенной длиной физического маятника?
4. Докажите справедливость утверждения: «Приведенная длина физического маятника всегда больше расстояния между точкой подвеса и центром масс маятника».
5. Что называется центром качания физического маятника?
6. Докажите справедливость утверждения: «Маятник, подвешенный в центре качания О', имеет такую же приведенную длину, какую он имел, когда был подвешен в исходной точке О».
7. Какой маятник называют оборотным? Как в данной работе с помощью оборотного маятника определяют величину ускорения свободного падения?
8. Тонкий однородный абсолютно твердый стержень, имеющий массу m и длину r, подвешен за один из своих краев. Найдите положение центра качания, соответствующего этой точке подвеса.
9. Физический маятник представляет собой однородное тело, обладающее центром симметрии. Докажите равенство периодов колебаний этого маятника для любых двух точек подвеса, равноотстоящих от центра масс и лежащих на прямой линии, проходящей через центр масс. Докажите, что эти две точки не обладают свойством взаимности. Имеется ли центр симметрии у физического маятника, использованного в настоящей работе?
Литература
1. Савельев И. В. Курс общей физики: Учебн. пособие для втузов: в 3 т. Т.1: 2.
2. Механика. Молекулярная физика. - 3-е изд., испр. - М.: Наука, 1986. – 432с.
3. Лабораторный практикум по физике: Учеб. пособие для студентов втузов/ Б. Ф. Алексеев, К. А. Барсуков, И. А. Войцеховская и др.; Под ред. К. А. Барсукова и Ю. И. Уханова. – М.: Высш. школа,1988. – 351 с.: ил.
ISBN 5-06-001365-0
4. Майсова Н.Н. Практикум по курсу общей физики. – М.: Высшая школа, 1970
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ СИСТЕМЫ ТЕЛ
С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА.
Цель работы – определить момент инерции системы четырех одинаковых грузов массы m двумя способами: 1) экспериментально с помощью маятника Обербека, 2) теоретически, считая грузы материальными точками. Сравнить полученные результаты.
Приборы и принадлежности: маятник Обербека, секундомер, масштабная линейка, набор грузов, штангенциркуль.
Теоретическое введение
Момент инерции – физическая величина, характеризующая инертность тела при вращательном движении.
Моментом инерции материальной точки относительно оси вращения называется произведение массы этой точки на квадрат ее расстояния до оси (см. рис. 1)

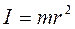
Моментом инерции произвольного тела относительно оси называется сумма моментов инерции материальных точек из которых состоит тело, относительно этой оси (см. рис. 2)
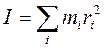
Для однородных тел правильной геометрической формы можно заменить суммирование интегрированием.
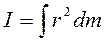 ,
,
где dm = ρdV (ρ – плотность вещества, dV– элемент объема)
Таким образом получены формулы некоторых тел массой m относительно оси, проходящей через центр тяжести:
а) стержня длиной 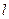 относительно оси, перпендикулярной стержню
относительно оси, перпендикулярной стержню
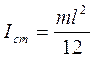 ,
,
б) обруча (а также тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча и проходящей через его центр тяжести (совпадающей с осью цилиндра)
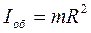 ,
,
где 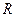 – радиус обруча (цилиндра)
– радиус обруча (цилиндра)
в) диска (сплошного цилиндра) относительно оси, перпендикулярной плоскости диска и проходящей через его центр тяжести (совпадающей с осью цилиндра )

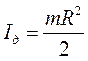 ,
,
где 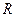 – радиус диска (цилиндра)
– радиус диска (цилиндра)
г) шара радиуса R относительно оси произвольного направления, проходящей через его центр тяжести
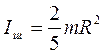 .
.
Момент инерции тела зависит: 1) от формы и размеров тела, 2) от массы и распределения масс, 3) от положения оси относительно тела.
Теорема Штейнера о параллельных осях записывается как:
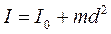 ,
,
где 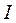 – момент инерции тела массой m относительно произвольной оси,
– момент инерции тела массой m относительно произвольной оси, 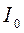 – момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно произвольной оси,
– момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно произвольной оси, 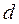 – расстояние между осями.
– расстояние между осями.
Описание установки
Маятник Обербека представляет собой крестовину, состоящую из шкива и четырех равноплечих стержней, закрепленных на горизонтальной оси (см. рис.2). На стержнях на равных расстояниях от оси вращения 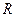 насажены четыре одинаковых груза массы m каждый. При помощи груза m1, прикрепленного к концу шнура, намотанного на один из шкивов, вся система может быть приведена во вращательное движение. Для отсчета высоты падения h груза m1 имеется вертикальная шкала.
насажены четыре одинаковых груза массы m каждый. При помощи груза m1, прикрепленного к концу шнура, намотанного на один из шкивов, вся система может быть приведена во вращательное движение. Для отсчета высоты падения h груза m1 имеется вертикальная шкала.
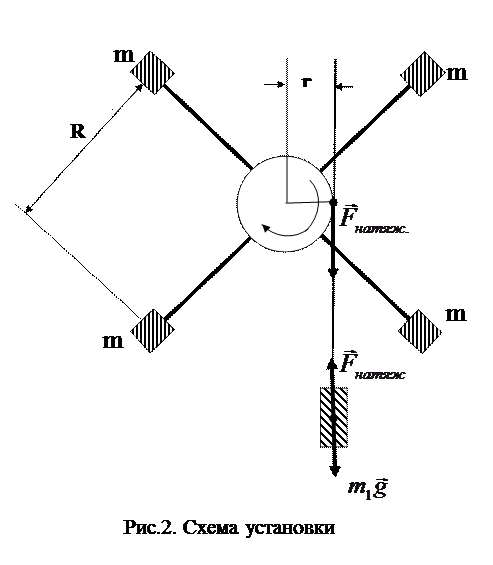 |
Запишем второй закон Ньютона для падающего груза в векторной форме 
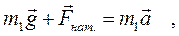 (1)
(1)
где 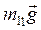 - сила тяжести;
- сила тяжести; 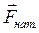 - сила натяжения шнура (см. рис. 1);
- сила натяжения шнура (см. рис. 1);
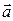 - линейное ускорение, с которым падает груз m1 вниз.
- линейное ускорение, с которым падает груз m1 вниз.
Принимая направление движения груза за положительное, перепишем уравнение (I) в скалярной форме
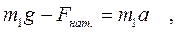 (2)
(2)
откуда получим выражение для силы натяжения шнура
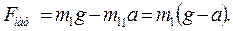 (3)
(3)
Линейное ускорение a находится из формулы пути равноускоренного движения без начальной скорости
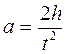 (4)
(4)
где h – высота падения груза m1; t – время падения.
Сила натяжения нити Fнат вызывает ускоренное вращение крестовины. Основной закон вращательного движения крестовины с учетом сил трения запишется так :
M – Mтр = I× i , (5)
где М – момент силы натяжения; Mтр - момент сил трения; I - момент инерции крестовины; i - угловое ускорение, с которым вращается крестовина. Величина момента сил трения Mтр по сравнению с величиной вращающего момента М невелика, и, следовательно, ею можно пренебречь.
Из уравнения ( 5 ) с учетом сделанного замечания получаем окончательную формулу для расчета момента инерции крестовины
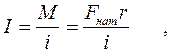 (6)
(6)
где r - радиус шкива. Угловое ускорение i определяется по формуле
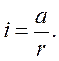 (7)
(7)
Подставляя (3) и (7) в (6), получаем окончательную формулу для расчета момента инерции крестовины
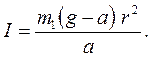 (8)
(8)
Порядок выполнения работы.
Часть I.
Экспериментальное определение момента инерции системы 4х грузов.
1. Снять со стержней грузы m .
2. Намотать в один слой шнур на шкив, установив груз m1 на заранее выбранной высоте h. Отпустив крестовину, замерить время падения tо груза с помощью секундомера. Опыт повторить пять раз (при одной и той же высоте падения h ).
3. Закрепить на концах стержней грузы m.
4. Выполнить операции, указанные в пункте 2, измеряя секундомером время падения t. Опыт повторить пять раз.
5. С помощью штангенциркуля измерить диаметр шкива d в пяти разных положениях.
6. Результаты измерений занести в таблицу. Найти приближенные значения и по методу Стьюдента оценить абсолютные погрешности измерения величин tо, t и d.
7. По формуле (4) рассчитать величину линейного ускорения a, с которым падает груз m1 для случаев:
а) крестовина без грузов (aо),
б) крестовина с грузами (а).
8. По формуле (8) вычислить момент инерции крестовины без грузов (Io) и с грузами (I), используя приближенные значения m1, R, g и полученные значения а и ао.
9. Вычислить погрешности измерений по формулам:
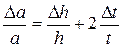 (9)
(9)
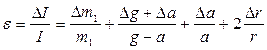 (10)
(10)
Таблица 1
Результаты измерений и вычислений
| № п/п | to, c | t, c | d, м | h, м | m = (0,144+0,005) кг m1 = (0,175+ 0,005) кг R = (0,220 + 0,003) м |
| Приближен. значения | |||||
| Абсолютная погрешность |
Часть II.
1. Теоретически найти момент инерции системы 4х грузов массы m, находящихся на расстоянии R от оси вращения (считая грузы материальными точками)
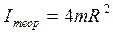 (11)
(11)
2. Сравнить результаты эксперимента и расчетов. Вычисть относительную погрешность
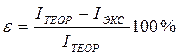 (12)
(12)
и сделать вывод о том, как велико расхождение полученных результатов.
Контрольные вопросы.
1. Что называется моментом инерции материальной точки и произвольного тела?
2. От чего зависит момент инерции тела относительно оси вращения?
3. Приведите примеры формул момента инерции тел. Как они получены?
4. Теорема Штейнера о параллельных осях и ее практическое использование.
5. Вывод формулы для расчета момента инерции крестовины с грузами и без грузов.
Литература
1. Савельев И. В. Курс общей физики: Учебн. пособие для втузов: в 3 т. Т.1: Механика. Молекулярная физика. - 3-е изд., испр. - М.: Наука, 1986. – 432с.
2. Детлаф А. А. , Яворский Б. М. Курс физики: Учебн. пособие для втузов. - М.: Высшая школа, 1989. - 607 с. - предм. указ.: с. 588-603.
3. Зисман Г. А., Тодес О. М.. Курс общей физики для втузов: в 3 т. Т. 1: Механика, молекулярная физика, колебания и волны - 4-е изд., стереотип. - М.: Наука, 1974. - 340 с.
4. Методические указания к выполнению лабораторных работ по разделу “Механика“.- Иваново, ИХТИ, 1989 г. (под редакцией Биргера Б.Н.).
Часть II. Колебания и волны
ОПРЕДЕЛЕНИЕ ЛОГАРИФМИЧЕСКОГО ДЕКРЕМЕНТА
КОЛЕБАНИЙ МАЯТНИКА
Цель работы: определить логарифмический декремент колебаний маятника при наличии разных сил сопротивления и построить графики изменения амплитуды колебаний со временем.
Приборы и принадлежности: маятник, кювета со шкалой, приспособление для пуска маятника, секундомер, емкость с водой.
Теоретическое введение
Колебаниями называются движения или процессы, повторяющиеся во времени. Простейшим видом колебательного движения является гармоническое колебание. Оно возникает в том случае, когда на тело, выведенное из положения равновесия, действует сила F, направленная к положению равновесия и пропорциональная смещению:
F = –kx, (1)
где х – смещение тела от положения равновесия, k – коэффициент пропорциональности, который зависит от упругих свойств системы и называется коэффициентом квазиупругой силы. Знак минус показывает, что сила направлена противоположно смещению.
Второй закон Ньютона для материальной точки, совершающей гармоническое колебание, представляет собой дифференциальное уравнение второго порядка
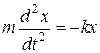 , (2)
, (2)
где m – масса материальной точки.
Решением уравнения (2) является выражение
x = Acos(wt + a), (3)
где A – амплитуда колебаний, w – циклическая частота, a – начальная фаза колебаний. Аргумент периодической функции
j = wt + a (4)
называется фазой колебаний. При t = 0 фаза j = a. Начало отсчета можно выбрать так, чтобы a = 0, тогда
x = Acoswt. (5)
График зависимости смещения х от времени t представляет собой график гармонического колебания (рис. 1).
Если колебания совершаются при наличии сил сопротивления, то энергия системы частично затрачивается на их преодоление. Вследствие этого амплитуда колебаний постепенно уменьшается, т.е. колебания будут затухающими.
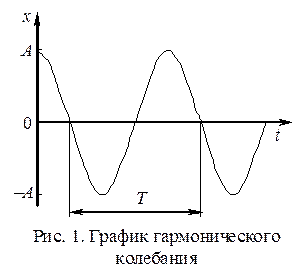 Таким образом, затухающие колебания совершаются при наличии двух сил: силы, возвращающей систему в положение равновесия, и силы сопротивления среды. При малых скоростях сила сопротивления прямо пропорциональна скорости υ:
Таким образом, затухающие колебания совершаются при наличии двух сил: силы, возвращающей систему в положение равновесия, и силы сопротивления среды. При малых скоростях сила сопротивления прямо пропорциональна скорости υ:
Fсопр = –rυ, (6)
где r – коэффициент сопротивления среды. Знак минус показывает, что сила сопротивления направлена в сторону, противоположную скорости.
Для затухающих колебаний второй закон Ньютона имеет вид:
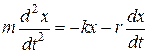 . (7)
. (7)
Решением уравнения (7) является выражение:
x = A0e–dtcos(wt + α), (8)
где A0 – начальная амплитуда колебаний; d– коэффициент затухания, равный
d =  ; (9)
; (9)
w – циклическая частота затухающих колебаний, равная w = 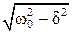 ; w0 – собственная частота колебаний системы. Собственнойчастотой колебаний называется частота колебаний в отсутствие сил сопротивления среды. Смещение колеблющейся системы в начальный момент времени равно
; w0 – собственная частота колебаний системы. Собственнойчастотой колебаний называется частота колебаний в отсутствие сил сопротивления среды. Смещение колеблющейся системы в начальный момент времени равно
x0 = A0cosα.
Из уравнения (8) видно, что амплитуда затухающих колебаний уменьшается с течением времени по экспоненциальному закону:
A = A0e–dt. (10)
График затухающего колебания представлен на рис. 2.
Кроме перечисленных выше величин A0, d, w, затухающие колебания характеризуются также логарифмическим декрементом D. Логарифмический декремент колебаний – безразмерная величина, равная натуральному логарифму отношения двух амплитуд, отстоящих друг от друга на время, равное одному периоду
D = 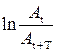 (11)
(11)
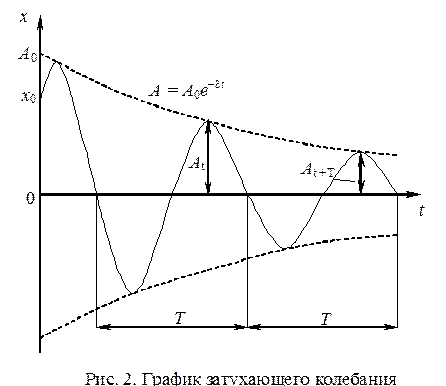
Из формулы (11) следует, что логарифмический декремент – величина, обратная числу колебаний Ne, за которое амплитуда уменьшается в е раз. Для характеристики колебательной системы также используется величина, называемая добротностью Q. При малых значениях логарифмического декремента (D << 1) добротность колебательной системы равна Q 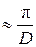 ,
,
тогда
Q = pNe.
Подставив в уравнение (11) At = A0e–dt и At + T = A0e–d(t +T), получим связь между параметрами затухающего колебания – логарифмическим декрементом, коэффициентом затухания и периодом колебаний:
D = dТ. (12)
Для определения логарифмического декремента нужно измерить амплитуды двух последовательных колебаний и взять натуральный логарифм их отношения. На опыте измеряют амплитуду в начальный момент времени A0 и амплитуду At через N полных колебаний.
Получим формулу для вычисления логарифмического декремента. Выразим отношение двух амплитуд:
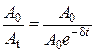 = eδt.
= eδt.
Так как t = NT, где N – число полных колебаний, Т – период колебаний, то 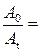 eδNT.
eδNT.
Используя соотношение (12), получим
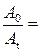 eDN.
eDN.
Найдем натуральный логарифм отношения амплитуд:
ln 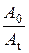 = lneDN = DN,
= lneDN = DN,
откуда
D = 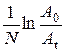 . (13)
. (13)
Описание установки
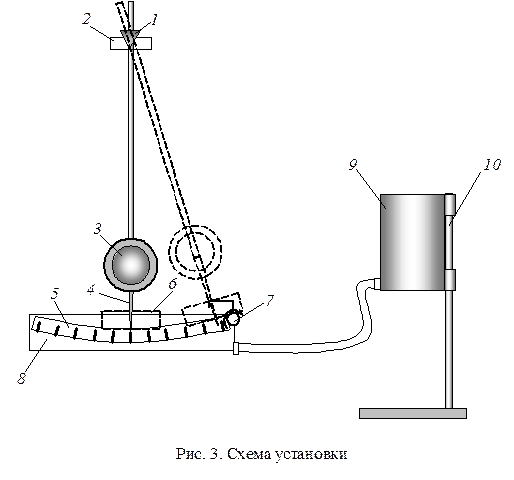
На рис. 3 изображена установка для наблюдения затухающих колебаний. Массивный маятник с длиной стержня около двух метров подвешен на треугольном стальном ноже 1, опирающемся на кронштейн 2. На стержне укреплен массивный диск 3. На нижнем конце стержня укреплен указатель 4 для отсчета числа делений по шкале 5. На стержне также закреплена лопатка 6. Маятник удерживается в отклоненном положении с помощью механического фиксатора 7. При повороте фиксатора маятник приходит в колебательное движение.
В работе изучаются затухающие колебания в воздухе и в воде. Чтобы заполнить кювету 8 водой, емкость 9 фиксируется в верхнем положении на кронштейне 10, и вода самотеком наливается в кювету через шланг.
Порядок выполнения работы
1. Установить маятник в крайнее правое положение с помощью фиксатора 7. Определить начальное значение амплитуды A0 по шкале и записать его.
2. Освободить маятник, повернув фиксатор, и одновременно включить секундомер. Вести отсчет числа колебаний маятника и через каждые 50 колебаний отмечать по шкале значение амплитуды колебаний Аt.
3. Через 250 колебаний остановить секундомер и записать его показание.
4. Наполнить сосуд водой и повторить опыт. Вести отсчет амплитуды через каждые 25 колебаний. Записать время 125 колебаний. В случае быстрого затухания амплитуду измерять чаще, например, через каждые 10 колебаний.
5. По формуле (13) рассчитать логарифмический декремент колебаний в воздухе и в воде.
6. Обработать результаты по методу Стьюдента. Записать приближенное значение логарифмического декремента колебаний в воздухе и в воде с указанием абсолютной и относительной погрешности.
7. По результатам измерений на одном графике построить зависимости амплитуды от времени для затухающих колебаний в воздухе и в воде.
8. Вычислить период колебаний маятника в воздухе и в воде.
9. Используя формулу (12) рассчитать коэффициент затухания колебаний маятника в воздухе и в воде.
10. Записать уравнения затухающих колебаний в виде (8), подставив в него полученные в работе величины A0, d, w и a.
11. Используя формулу (9), рассчитать коэффициент сопротивления среды (воздуха и воды).
12. Сделать выводы по работе.
Таблица
Результаты измерений и вычислений
| № п/п | В воздухе | В воде | ||||||
| А0 | Аt | N | D | А0 | Аt | N | D | |
| Среднее значение D | Среднее значение D | |||||||
| Абсолютная погрешность DD | Абсолютная погрешность DD |
Контрольные вопросы и задания
1. Какие колебания называются гармоническими? Под действием какой силы они происходят? Запишите второй закон Ньютона для гармонических колебаний.
2. Запишите уравнение смещения от времени для гармонического колебания. Перечислите величины, характеризующие гармоническое колебание. Изобразите график гармонического колебания.
3. Какие колебания называются затухающими? Запишите второй закон Ньютона для затухающих колебаний.
4. Запишите уравнение смещения от времени для затухающего колебания. Перечислите величины, характеризующие затухающее колебание. Изобразите график затухающего колебания.
5. Дайте определение логарифмического декремента колебаний. Каков его физический смысл? Как он определяется в данной работе, от чего зависит?
Литература
1. Савельев И. В. Курс общей физики: Учебн. пособие для втузов: в 3 т. Т.1: Механика. Молекулярная физика. - 3-е изд., испр. - М.: Наука, 1986. – 432с.
2. Детлаф А. А. , Яворский Б. М. Курс физики: Учебн. пособие для втузов. - М.: Высшая школа, 1989. - 607 с. - предм. указ.: с. 588-603.
3. Майсова Н.Н. Практикум по курсу общей физики. – М.: Высшая школа, 1970
4. Лабораторный практикум по физике: Учеб. пособие для студентов втузов./ Ахматов А.С., Андреевский В.М., Кулаков А.И. и др.; Под редакцией А.С. Ахматова. – М.: Высшая школа. 1980. – 360 с.
ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКА В ВОЗДУХЕ
МЕТОДОМ СТОЯЧИХ ВОЛН
Цель работы: определение длины стоячей волны и скорости звука в воздухе.
Приборы и принадлежности: резонатор с телефоном и микрофоном, звуковой генератор, осциллограф, отсчетная линейка.
Теоретическое введение
Звук представляет собой упругие волны, распространяющиеся в газах, жидкостях и твердых телах и воспринимаемые ухом человека и животных. Человеческое ухо способно воспринимать звук с частотами от 16 Гц до 20 кГц. Звук с частотами ниже 16 Гц называется инфразвуком, а выше 20 кГц – ультразвуком. Наука о звуке называется акустикой.
Если в упругую среду поместить источник колебаний, то соприкасающиеся с ним частицы будут выведены из положения равновесия и придут в колебательное движение. Колебания этих частиц передаются силами упругости соседним частицам среды, а от них – к другим, более удаленным от источника колебаний. Через некоторое время колебательный процесс охватит всю среду. Распространение колебаний в упругой среде называется волнойили волновым процессом.
Различают продольные волны (частицы колеблются вдоль направления распространения волны) и поперечные волны (частицы колеблются перпендикулярно этому направлению). Продольные волны представляют собой чередующиеся сгущения и разрежения. Такие волны распространяются в средах, в которых возникают силы упругости при деформациях сжатия и растяжения, но не обладающих напряжением сдвига (т.е. в твердых телах, жидкостях и газах). Примером продольных волн являются звуковые волны. Поперечные волны распространяются в средах, в которых возникают упругие силы при деформации сдвига (т.е. в твердых телах или в некоторых особых случаях, например, волны на границе раздела жидкость-газ). Скорость распространения продольных и поперечных волн зависит от упругих свойств среды. Так, при 20 ºС скорость звука в воздухе равна 343 м/c, в в
