Абстрактное векторное пространство

Восемь свойств сложения и умножения, установленных в геометрической модели, позволяют построить арифметическую модель и называются аксиомами векторного пространства.

Рассмотрим примеры моделей, удовлетворяющих этим аксиомам.

Пример 1.

Множество многочленов степени не выше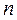

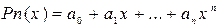
образует векторное пространство, в котором мономы 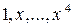– базисные элементы, а коэффициенты многочлена 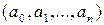– координаты вектора 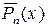в этом базисе.

Пример 2.

Пусть 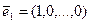, ,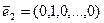…, 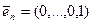- « -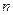местные наборы», 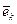имеет 1 на 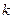-м месте и нули на остальных местах, 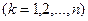. Тогда объекты

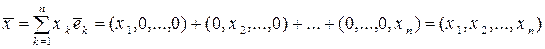
образуют векторное пространство с базисными элементами 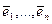. Обозначим это пространство .

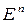Векторное пространство 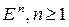, позволяет определить размерность всякого векторного пространства 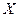при помощи следующей аксиомы.

9. Аксиома размерности. Существует изоморфизм .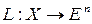

Определение абстрактного векторного пространства.

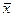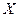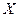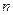Пусть для элементов множества выполняется 8 аксиом векторного пространства и аксиома размерности. Тогда есть -мерное абстрактное векторное пространство, а 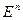является его арифметической моделью.

Элементы множества 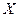могут быть произвольной природы. Например:

· выборки 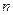измерений ;

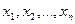· цены 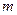наименований ;

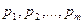· наборы продуктов, расстояния между заводом изготовителем и сырьевыми складами и т.д.

Следствие.

Все 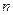-мерные векторные пространства имеют одну и ту же арифметическую модель, поэтому изоморфны.

Множество многочленов степени не выше 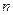в примере 1 образуют 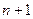-мерное пространство. Изоморфизм, устанавливающий размерность, задается в этом случае так

, .

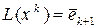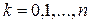Здесь 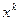– мономы, а 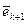– базисные орты в .

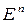Если векторное пространство 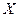содержит для всякого 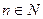подмножество, 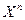, которое само является векторным пространством и для него выполняется аксиома размерности с заданным 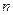, то 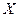назовем бесконечным векторным пространством. Примером такого пространства является множество всех многочленов. Подмножества многочленов степени не выше 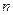образуют 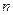-мерные подпространства в этом пространстве.

Аксиомы скалярного произведения векторов.

Модель 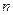-мерного пространства 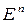не содержит понятия длинны вектора при 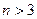. Для определения длинны вектора в 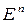при 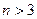воспользуемся связью между длинной вектора и скалярным произведением. При этом скалярное произведение зададим аксиоматически теми свойствами, которыми оно определяется в трехмерном векторном пространстве.

Напомним, что в геометрической модели трехмерного скалярного произведения задается представлением

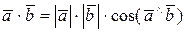(4)

В школьном курсе геометрии из этого представления выводятся три свойства:

1) 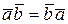, 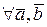(5)

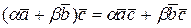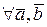2) , и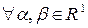

3) ; .

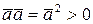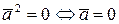Следствие.

Из формулы (4) находим представление длины вектора через скалярное произведение

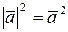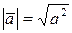, (6)

Если в качестве базиса выбрать векторы 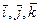, то используя свойства 1-3 находим координатное представление скалярного произведения:

,

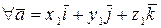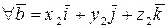
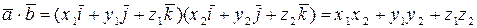(7)

Мы воспользовались тем, что , .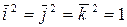

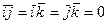Следствие.

Используя (6) и (7), заключаем, что

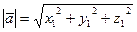(8)

Схему, по которой мы из определения скалярного произведения (4) получили формулу длины вектора (8), повторим в абстрактном векторном пространстве с той разницей, что: 1) скалярное произведение векторов зададим при помощи трех аксиом 5 и 2) существование скалярного произведения в координатной модели 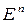установим формулой, аналогичной (7):

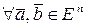
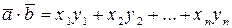(9)

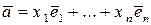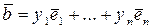где , в .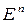

Теперь, согласно нашей схеме, длинна вектора определена формулой (6). Из (6) с учетом (9) получаем формулу длинны вектора в 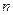-мерном арифметическом пространстве аналогичную (8) в виде

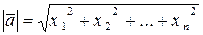. (10)

Вывод 4.

В трехмерном векторном пространстве длина вектора (8) находится благодаря теореме Пифагора. В абстрактном векторном пространстве размерности больше трех аксиомами (5) задается скалярное произведение, а длина выражается через скалярное произведение по формуле (6). В арифметической модели 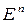скалярное произведение существует в виде (9), а длина вектора определяется согласно формуле (10).

Определение.

Абстрактное 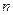-мерное векторное пространство, в котором задано скалярное произведение векторов, удовлетворяющее трем аксиомам (5) называем 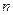-мерным векторным евклидовым пространством. Его координатная модель 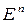со скалярным произведением (9) называется декартовой моделью. (Рене Декарт (1596-1650) впервые ввел координатную модель трехмерного евклидова пространства).