Разностная схема решения уравнения теплопроводности

КУРСОВОЙ ПРОЕКТ (РАБОТА)

По дисциплине: Программные продукты
в математическом моделировании

^{(наименование учебной дисциплины согласно учебному плану)}

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Тема: «Численное решение уравнения теплопроводности»

Вариант №20

Автор: студент гр. _ЭХТ-11-1__ _________________ /_Чикуров Р.О./

^{(подпись) (Ф.И.О.)}

ОЦЕНКА: _____________

Дата: ______________

ПРОВЕРИЛ

Руководитель проекта доцент ________________ /Певнева А.Г./

^{(должность) (подпись) (Ф.И.О.)}

Санкт-Петербург,

2013 год

Министерство образования и науки Российской Федерации
Национальный минерально-сырьевой университет "Горный"
		УТВЕРЖДАЮ Заведующий кафедрой   /_____________/ доц. Маховиков А.Б./   "___"__________2012 г.

Кафедра: _____________Информатики и компьютерных технологий_____________

КУРСОВАЯ РАБОТА

по дисциплине ___________________ИНФОРМАТИКА ______________________

^{(наименование учебной дисциплины согласно учебному плану)}

ЗАДАНИЕ

студенту группы _____ЭХТ-11-1____ ___Чикуров Р.О.__

^{(шифр группы) (Ф.И.О.)}

1) Тема работы: Численное решение уравнения теплопроводности средствами табличного процессора Microsoft Excel и пакета математических расчетов MathCAD.

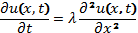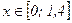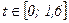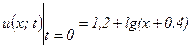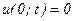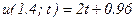2) Исходные данные к работе: Найти приближенное решение уравнения теплопроводности для значений аргументов , при заданных начальном и граничных и условиях средствами табличного процессора Microsoft Excel и пакета математических расчетов MathCAD. Принять 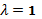, шаг изменения пространственной координаты равным 0.1, временной – 0.2. Получить максимальное и минимальное значения температуры в рассмотренной области, построить графики изменения температуры в точки области x=0,9 и при значении времени t=1,4.

3) Содержание пояснительной записки: Пояснительная записка включает в себя задание на выполнение работы, титульный лист пояснительной записки, аннотацию, оглавление, введение, собственно текст пояснительной записки, вывод, список использованных источников.

4) Перечень графического материала: 25 рисунков

5) Срок сдачи законченной работы:

Руководитель проекта: доцент ______________ /Певнева А.Г./

^{(должность) (подпись) (Ф.И.О.)}

Дата выдачи задания: 14.02.2013

Аннотация

В данном курсовом проекте выполнен расчет уравнения теплопроводности с начальным и граничными условиями. C помощью дифференциальных уравнений в частных производных получены максимальное и минимальное значения температуры в рассмотренной области. Для получения численных значений искомых величин по этим выражениям проведён расчёт и построены графики исследуемых величин средствами табличного процессора Microsoft Excel и пакета математических расчетов MathCAD. В специальной части проекта представлено решение уравнения разностным методом.

Работа содержит 25 страниц и 25 рисунков.

Abstract

The subject of this coursework is the solution of heat-transfer equation to the initial and boundary conditions. To obtain the numerical values ​​of the unknown quantities in these expressions were calculated and constructed diagrams of the studied variables by means of spreadsheet Microsoft Excel, a package of mathematical calculations MathCAD. In the special part of the project there is a solution to heat-transfer equation is presented in different methods.

The project contains 25 pages, including 25 pictures.

.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ.. 5

1. РАЗНОСТНАЯ СХЕМА РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ.. 6

2. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ТАБЛИЧНОМ ПРОЦЕССОРЕ MICROSOFT EXCEL.. 10

3. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПАКЕТЕ МАТЕМАТИЧЕСКИХ РАСЧЕТОВ MATHCAD.. 18

4. АНАЛИЗ РЕЗУЛЬТАТОВ РАСЧЕТА.. 24

ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА.. 25

ВВЕДЕНИЕ

Движение систем малого числа частиц математически описывают, как правило, обыкновенными дифференциальными уравнениями. Если число очень велико, то следить за движением отдельных частиц практически невозможно. При этом удобнее рассматривать систему частиц как сплошную среду, характеризуя ее состояние средними величинами: плотностью, температурой в точке и т.д. Математические модели сплошной среды приводят к уравнениям в частных производных, которым удовлетворяют упомянутые средние величины. К уравнениям в частных производных приводят задачи газодинамики, теплопроводности, переноса излучения, распространения нейтронов, теории упругости, электромагнитных молей, процесса переноса в газах, квантовой механики и многие другие. Независимыми переменными в физических задачах задаются, как правило, время и координаты. Бывают и другие переменные, например, скорости частиц в задачах переноса. Решение требуется найти в некоторой области изменения независимых переменных. Полная постановка задачи содержит дифференциальное уравнение и дополнительные условия, позволяющие выделить единственное решение из семейства решений дифференциального уравнения. Дополнительные условия задаются, как правило, на границе рассматриваемой области. Если одной из независимых переменных является время, то решение ищут в некоторой пространственной области на отрезке времени 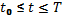. В этом случае дополнительные условия, заданные при 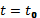называют начальными, а дополнительные условия, заданные на границе области – граничными или краевыми.

Точные методы позволяют получить явное выражение решения через начальные данные, однако они применимы для очень узкого класса задач. Численные методы являются основным способом решения дифференциальных уравнений в частных производных.

РАЗНОСТНАЯ СХЕМА РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ

Рассмотрим численное решение уравнения теплопроводности:

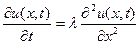, (1.1)

где u – температура, x – пространственная координата, t – время, 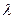– коэффициент температуропроводности.

Решение нужно получить для значений аргументов 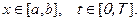В начальный момент времени (t=0) известно распределение температуры:

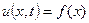(1.2)

Задаются также значения функции на концах промежутка интегрирования пространственной координаты, т.е. 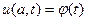и 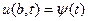. (1.3)

В математике доказано, что задача, состоящая из уравнения (1.1), начального условия (1.2) и граничных условий (1.3), является корректно поставленной и имеет единственное решение. Численное решение получим разностным методом, который применяли к решению краевой задачи обыкновенного дифференциального уравнения II порядка. Для того, чтобы написать разностную схему, приближенно описывающую дифференциальное уравнение, необходимо свершить два шага:

1) заменить область непрерывного изменения аргументов областью дискретного его изменения;

2) заменить дифференциальный оператор некоторым разностным соотношением и сформулировать разностный аналог для краевых и начального условий.

В результате приходим к системе линейных алгебраических уравнений относительно значений решения дифференциального уравнения в отдельных точках области определения аргументов. Таким образом, задача о численном решении дифференциального уравнения сводится к вопросу нахождения решения системы линейных алгебраических уравнений.

Произведем замену частных производных 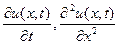конечными разностям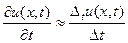и: и 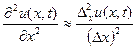(1.4),

где приращение аргументов по времени и по пространственной координате принимаются постоянными, равным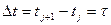и и 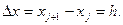Подставляя соотношения (1.4) в дифференциальное уравнение с частными производными (1.1), получаем разностные уравнения для искомого решения 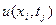на сетке значений аргумента по пространственной 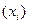и временной 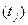переменным: 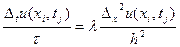(1.5)

Разность первого порядка по времени заменяется разностями

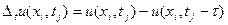. (1.6)

Разность второго порядка по пространственной координате заменяется разностями 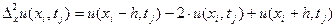. (1.7)

Аналогичные разностные соотношения делений применились при решении краевой задачи обыкновенных дифференциальных уравнений второго порядка. Поставив соотношение (1.6) и (1.7) в уравнения (1.5), приходим к системе алгебраических уравнений относительно значений температуры в узлах :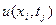

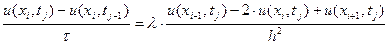, (1.8)

где i=1,2,… m-1 и j=1,2,…n. Здесь m и n число делений промежутка изменения пространственной и временной переменных.

Уравнения (1.8) позволяют вычислить решение во внутренних точках сетки области определения решения. Недостающие уравнения находятся из начального (1.2) и граничных (1.3) условий.

Начальное условие (2) при t=0 в точках x_i имеют вид: 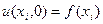(1.9)

Для значений на концах изменения пространственной переменной (1.3) имеем :

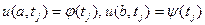(1.10)

Разностная схема (1.8) носит название неявной разностной схемы. Значения искомой функции при одном значении временной переменной называются слоем. Начальное условие (1.9) задает значения решения на начальном (нулевом) слое. Значения решения на первом слое полностью определяется значениями на нулевом (при t=0). Для этого нужно решить систему уравнений (1.8), подставив известные значения при t=0. Полученные значения становятся исходными значениями для определения решения на втором временном слое как решения системы (1.8) при известном значении решения при 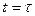(шаге изменения временной переменной). Этот процесс повторяется до полного вычисления решения на всех слоях.

Рассмотрим численное решение для уравнения теплопроводности (1.1) при изменении аргумента х от нуля до единицы, времени t от нуля до 1,2 при начальном условии: 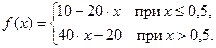(1.11)

и граничных условиях: 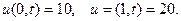(1.12)

Положим коэффициент температуропроводности равным единице, шаг по пространственной координате – 0,1, по временной координате – 0,2.

Разностное уравнение (1.8) преобразуем таким образом, чтобы искомые решения одного слоя находились по одну сторону от знака равенства:

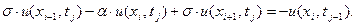(1.13)

Здесь введены обозначения: 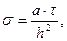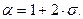(1.14)

Граничные условия имеют вид:

u(0,0)= u(0,0.2)= u(0,0.4)=u(0,0.6)=u(0,0.8)=u(0,1.0)=u(0,1.2)=10 (1.15)

u(1,0)= u(1,0.2)= u(1,0)= u(1,0.4)= u(1,0.6)= u(1,0.8)= u(1,1.0)= u(1,1.2)=20 (1.16)

На каждом временном слое необходимо решить систему (1.13) из девяти уравнений. Перепишем систему (1.13) в развернутом виде:

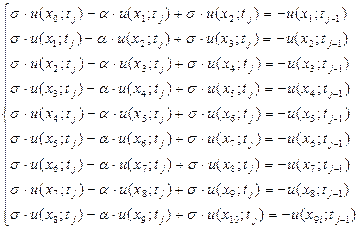(1.17)

Преобразуем систему (1.17), учитывая, что граничные значения заданы и известны (1.15), (1.16).

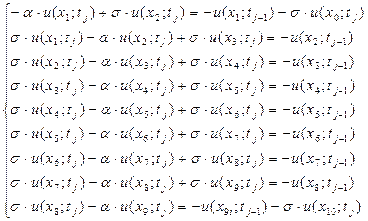(1.18)

Для вычисления решения в узловых точках одного временнóго слоя 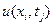при i=1,2..m-1 получили систему линейных алгебраических уравнений с матрицей коэффициентов трехдиагонального вида. Решение этой системы можно производить любым из известных методов решения: Гаусса, Крамера, с использованием обратной матрицы, прогонки, а также итерации. Полученное решение для одного слоя используется при получении решения для следующего временного слоя.

Следовательно, получение решения уравнения (1.1) с начальным и граничными условиями (1.2), (1.3) свелось к решению нескольких систем линейных алгебраических уравнений (1.18) с одной системой коэффициентов перед неизвестными и различными правыми частями уравнений системы.

Решение будем выполнять в табличном процессоре Microsoft Excel методом прогонки и в пакете математических расчетов MathCAD.