Фазочастотные искажения

На рис. 2.12 проиллюстрированы фазочастотные искажения.

Пусть входной сигнал 3 состоит из двух гармонических составляющих 1 и 2, причем вторая гармоника отстает от первой на p/2 (рис. 2.12,а). В процессе усиления изменилось фазовое соотношение между гармоническими составляющими, и вторая гармоника стала совпадать по фазе с первой, в результате форма кривой сигнала на выходе 3 изменилась (рис. 2.12,б).

Фазовый сдвиг j между выходным и входным напряжениями усилителя равен алгебраической сумме фазовых сдвигов, создаваемых отдельными каскадами:

j = j ₁ + j ₂ + j ₃ +… . (2.12)

Это свойство вытекает их того, что коэффициент передачи усилителя равен произведению коэффициентов передачи отдельных каскадов:

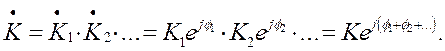(2.13)

При постоянном значении коэффициента усиления форма кривой сигнала не искажается, если фазовый угол изменяется прямо пропорционально частоте, т.е.

j = af, (2.14)

где а – любое постоянное число, включая нуль.

Уравнение (2.14) и является уравнением идеальной фазовой характеристики. Действительно, если на входе усилителя поддерживается напряжение

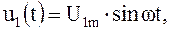
то напряжение на выходе будет изменяться по закону

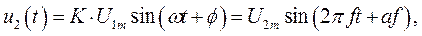
т.е.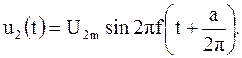

Последнее равенство показывает, что независимо от частоты выходное напряжение опережает входное при а > 0 или отстает от него при а < 0 на некоторое время фазового пробега t_Ф = – а/2π ; при этом взаимное расположение синусоид различных частот, а следовательно, и форма кривой не изменяются.

Так как напряжение на выходе не может возникнуть раньше, чем на входе, то при существовании зависимости j = af всегда a £ 0. Следовательно, если K = const, то единственной причиной линейных фазо-частотных искажений сигналов является отступление от уравнения (2.14) идеальной фазовой характеристики [2].

2.4.4. Нелинейные искажения гармонического сигнала

Эти искажения обусловлены нелинейной характеристикой передачи S_ВЫХ (S_ВХ). Основные виды нелинейных искажений показаны на рис. 2.13.

Пусть S_ВХ = S_msin ωt.

При квадратичной нелинейности

S_ВЫХ = aS_ВХ + bS_ВХ² .

S_ВЫХ = aS_msin ωt + 0,5·bS_m² - 0,5·bS_m² cos 2ωt = S₀ + S₁ sin ωt + S₂cos 2ωt.

При кубической нелинейности

S_ВЫХ = aS_ВХ + bS_ВХ³.

S_ВЫХ = aS_msin ωt + 0,75·bS_m³ sin ωt - 0,25·bS_m³ sin 3ωt = S₁ sin ωt + + S₃ sin 3 ωt .

а)	б)
в)	г)
Рис. 2.13. Виды нелинейных искажений: кубическая нелинейность (а); квадратичная нелинейность (б); отсечка (амплитудное ограничение) (в); центральная отсечка (г)

Учитывая сказанное, можно сделать следующие выводы.

· При нелинейных искажениях гармонического сигнала продуктами искажений являются высшие гармоники сигнала.

· Члены аппроксимирующего полинома с чётными степенями S_ВХ обусловливают чётные гармоники S_ВЫХ, а с нечётными степенями S_ВХ - нечётные гармоники S_ВЫХ.

· Номер высшей гармоники равен показателю степени аппроксимирующего полинома.

· Если характеристика передачи – нечётная функция, то S_ВЫХ симметрична относительно оси абсцисс и не содержит постоянной составляющей и чётных гармоник.

2.4.5. Коэффициент гармоник

Нелинейные искажения гармонического сигнала оценивают коэффициентом гармоник К_Г или коэффициентом нелинейных искажений К_НИ :

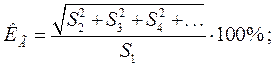(2.15)

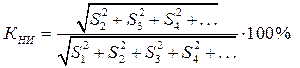. (2.16)

При аналитических измерениях нелинейных искажений, в том числе при компьютерном моделировании используют выражение (2.15); при аппаратурных измерениях – выражение (2.16). Практически при К_Г ≤ 30% результаты совпадают, К_Г ≈ К_НИ.

2.4.6. Графоаналитические методы измерений нелинейных искажений

Для расчёта К_Г пользуются приближенными графоаналитическими методами.

1. Если характеристику передачи можно аппроксимировать квадратичным полиномом (рис. 2.13,б), то есть допустимо пренебречь гармониками выше второй, применяют метод трёх ординат (рис. 2.14).

U_ВЫХ = U_СР + U_m1 cos ωt +U_m2 cos2ωt ;

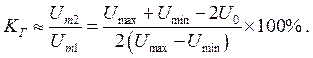(2.17)

2. Для определения первых четырёх гармоник используют метод пяти ординат (рис. 2.15).

U_ВЫХ = U_СР + U_m1 cos ωt + U_m2 cos 2ωt + U_m3 cos3ωt + U_m4 cos 4ωt ;

U_СР = [U_max + U_min + 2(U₁ + U₂)] / 6 ;

U_m1 = (U_max – U_min + U₁ – U₂) / 3 ;

U_m2 = (U_max + U_min – 2U₀) / 4 ;

U_m3 = [U_max – U_min - 2(U₁ – U₂)] / 6 ;

U_m4 = [U_max + U_min – 4(U₁ + U₂) + 6 U₀] / 12 .

Проверка:

U_СР + U_m1+ U_m2+ U_m3+ U_m4 = U_max . (2.18)

Можно ли определить К_Г системы из n последовательно включённых усилителей? В общем виде – нельзя. Иногда оценивают:

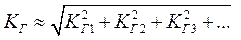. (2.19)

2.4.7. Нелинейные искажения негармонического сигнала

Нелинейные искажения негармонического сигнала дают весьма сложный спектр продуктов искажений.

Пусть S_ВХ = S_m1 sin ω₁t + S_m2 sin ω₂t .

Подадим S_ВХ на вход устройства с характеристикой передачи:

S_ВЫХ = a S_ВХ + b S_ВХ² + c S_ВХ³ + … .

Первое слагаемое в выражении S_ВЫХ даст сигнал а sin ω₁t + а sin ω₂t с двумя частотами ω₁ , ω_{2 .}

Второе слагаемое S_ВЫХ даст сигнал b(sin ω₁t + sin ω₂t)² с четырьмя частотами 2ω₁ , 2ω_{2 ,} (ω₁ + ω₂), (ω₁ – ω₂).

Третье слагаемое S_ВЫХ даст сигнал с(sin ω₁t + sin ω₂t)³ с восемью частотами ω₁ , ω_{2 ,} 3ω₁ , 3ω_{2 ,} (2ω₁ + ω₂), (2ω₁ – ω₂), (ω₁ + 2ω₂), (ω₁ – 2ω₂), и т.д.

Таким образом, спектр продуктов искажений сложного сигнала содержит, кроме гармоник составляющих S_ВХ , много составляющих вида m ω_k + n ω_i .

Например, если S_ВХ содержит 2 частоты: 100 и 170 Гц, а S_ВЫХ аппроксимируется полиномом третьей степени, то в спектре S_ВЫХ будут присутствовать 12 частот: 30, 70, 100, 170, 200, 240, 300, 340, 370, 440, 510 Гц.