Способ сравнения деформаций

Выполняя решение уравнения 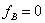, названного уравнением совместности деформаций, можно рассуждать следующим образом.

Прогиб точки В основной системы под действием нагрузок q и В складывается из двух прогибов: одного 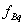, вызванного лишь нагрузкой q, и другого 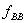, вызванного реакцией В. Таким образом,

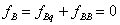(1)

Остается вычислить эти прогибы. Для этого загрузим основную систему одной нагрузкой q (рис.4, а).

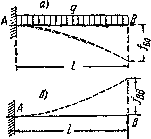
Рис.4. Расчет прогиба от исходной нагрузки — а) и реакции — б)

Тогда прогиб точки В будет равен:

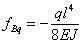
При нагружении основной системы реакцией В (Рис.4,б) имеем:

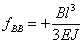
Подставляя эти значения прогибов в уравнение (1), получаем:

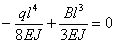
Отсюда

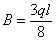
В этом способе мы сначала даем возможность основной системе деформироваться под действием внешней нагрузки q, а затем подбираем такую силу В, которая бы вернула точку В обратно. Таким образом, мы подбираем величину неизвестной дополнительной реакции В с тем расчетом, чтобы уравнять прогибы от нагрузки q и силы В. Этот способ и называют способом сравнения деформаций.

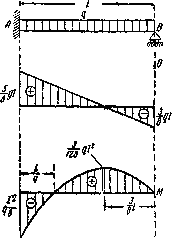
Рис.5. Эпюры поперечных сил и внутренних изгибающих моментов.

Подставляя значение лишней реакции В в уравнения статики, получаем

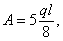
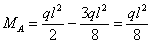
Выражение изгибающего момента получаем, рассматривая правую часть балки (Рис.4) и подставляя значение В:

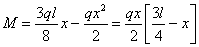
Поперечная сила Q выражается формулой

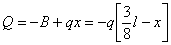
Эпюры моментов и поперечных сил изображены на рис.5. Сечение с наибольшим положительным моментом соответствует абсциссе 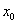, определяемой равенством

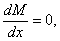т.е.

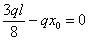
Отсюда 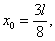соответствующая ордината эпюры моментов, равна:

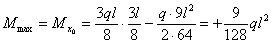
Лекция № 36. Применение вариационных методов.

Раскрытие статической неопределимости для балки, может быть произведено и при помощи теоремы Кастильяно.

«Лишнюю» опорную реакцию В (Рис.1, а) заменяем «лишней» неизвестной силой В, действующей вместе с заданной нагрузкой q на основную статически определимую балку АВ (фиг. 361, б).

Рис.1. Исходная, а) и основная — б) расчетные схемы

Дифференцируя по силе В потенциальную энергию и вычисляя таким образом прогиб 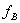, следует 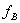приравнять нулю.

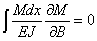(1)

Остается вычислить М и 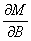, установить пределы интеграла и взять его.

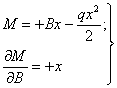
Будем считать, что сечение балки не меняется по длине. Тогда уравнение (1) примет вид:

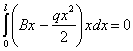или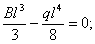

отсюда

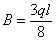
Далее решение не отличается от описанного в способе сравнения деформаций.

Раскрытие статической неопределимости возможно выполнить также и по теореме Мора. При решении по Мору, кроме первого состояния нагружения основной балки заданной нагрузкой и лишней неизвестной силой (Рис.2, а), следует показать ту же балку во втором состоянии загружения — силой 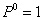(Рис.2,б).

Вычисления при обозначениях, принятых на Рис. 2, дают:

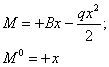
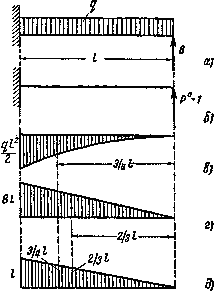
а) исходная модель, б) фиктивная модель нагружения, в) грузовая эпюра моментов, г) эпюра моментов от реакции В, д) единичная эпюра моментов

Рис.2. Решение методом Мора и Верещагина

т.е. то же, что и при использовании теоремой Кастильяно.

При решении того же примера по способу Верищагина к двум схемам состояний загружения (Рис.2 а и б) следует построить эпюры моментов: от нагрузки q (Рис.2, в) от силы B (Рис.2 г), и от силы 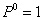(Рис.2, д).

Величина моментных площадей:

от нагрузки q:

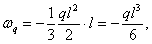
от нагрузки В:

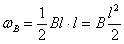
Ординаты эпюр единичной нагрузки:

для умножения на :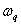

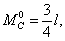
для умножения на :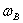

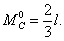
Прогиб в точке В

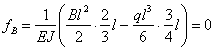
Отсюда

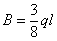
Совпадение результатов расчета опорной реакции очевидно.