Как проводится испытание материала на растяжение?
Механические характеристики материала определяются в результате испытания образца на специальных прессах. Форма образца может быть различной. Как правило, это стержень с участком постоянного поперечного сечения (круглого или прямоугольного) длиной 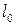 . Концы образца имеют специальные утолщения для их закрепления в испытательной машине.
. Концы образца имеют специальные утолщения для их закрепления в испытательной машине.
Перед началом испытания замеряется площадь поперечного сечения средней части образца 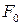 . Значения растягивающей силы P и удлинения средней части образца
. Значения растягивающей силы P и удлинения средней части образца 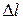 в каждый момент нагружения определяются специальными устройствами. При испытании нагрузка увеличивается медленно и плавно. Современные испытательные машины снабжены записывающим прибором, который при испытании образца автоматически вычерчивает график зависимости между нагрузкой P и абсолютным удлинением
в каждый момент нагружения определяются специальными устройствами. При испытании нагрузка увеличивается медленно и плавно. Современные испытательные машины снабжены записывающим прибором, который при испытании образца автоматически вычерчивает график зависимости между нагрузкой P и абсолютным удлинением 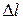 . Такой график называется диаграммой растяжения. Идея построения такого графика была предложена Яковом Бернулли, поэтому он иногда называется диаграммой Бернулли.
. Такой график называется диаграммой растяжения. Идея построения такого графика была предложена Яковом Бернулли, поэтому он иногда называется диаграммой Бернулли.
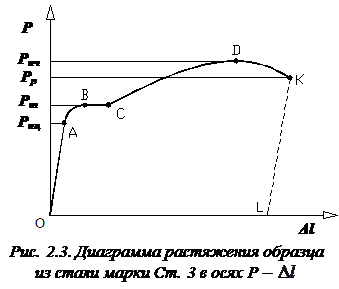 Рассмотрим, например, диаграмму растяжения образца, изготовленного из стали марки Ст. 3 (рис. 2.3). Заметим, что эта диаграмма характеризует поведение именно образца, а не материала, из которого он сделан.
Рассмотрим, например, диаграмму растяжения образца, изготовленного из стали марки Ст. 3 (рис. 2.3). Заметим, что эта диаграмма характеризует поведение именно образца, а не материала, из которого он сделан.
В начальной стадии испытания, до точки А с ординатой 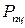 (индекс «пц» – сокращение от слова пропорциональность), зависимость между силой P и удлинением
(индекс «пц» – сокращение от слова пропорциональность), зависимость между силой P и удлинением 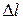 носит линейный характер, то есть удлинение образца растет пропорционально росту внешней нагрузки. Этот факт свидетельствует о линейной деформируемости образца. Затем диаграмма искривляется и при некотором значении растягивающей силы
носит линейный характер, то есть удлинение образца растет пропорционально росту внешней нагрузки. Этот факт свидетельствует о линейной деформируемости образца. Затем диаграмма искривляется и при некотором значении растягивающей силы 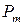 (индекс «т» – сокращение от слова текучесть) наблюдается значительный рост удлинения образца без увеличения нагрузки. Это явление называется текучестью. Практически горизонтальный участок диаграммы BC называется площадкой текучести, а точка B – критической точкой диаграммы. При некотором значении растягивающей силы
(индекс «т» – сокращение от слова текучесть) наблюдается значительный рост удлинения образца без увеличения нагрузки. Это явление называется текучестью. Практически горизонтальный участок диаграммы BC называется площадкой текучести, а точка B – критической точкой диаграммы. При некотором значении растягивающей силы 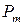 , соответствующем критической точке B, на поверхности образца, если он, например, полирован, мы заметим появление сначала нескольких полосок, параллельных между собой и расположенных под углом примерно
, соответствующем критической точке B, на поверхности образца, если он, например, полирован, мы заметим появление сначала нескольких полосок, параллельных между собой и расположенных под углом примерно 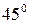 к оси образца. Далее появляется вторая система линий, пересекающая первую и наклоненную к оси под тем же углом, что и первая. Такая система сопряженных линий называется линиями Людерса – Чернова. Эти линии впервые были описаны в 1859 г. немецким металлургом В. Людерсом и независимо от него в 1884 г. русским металлургом Д.К. Черновым (1839 – 1921 гг.).
к оси образца. Далее появляется вторая система линий, пересекающая первую и наклоненную к оси под тем же углом, что и первая. Такая система сопряженных линий называется линиями Людерса – Чернова. Эти линии впервые были описаны в 1859 г. немецким металлургом В. Людерсом и независимо от него в 1884 г. русским металлургом Д.К. Черновым (1839 – 1921 гг.).
Упомянутые линии представляют собой следы сдвигов частиц материала. Направления этих линий соответствуют площадкам, на которых при растяжении возникают наибольшие касательные напряжения.
За точкой C удлинение образца начинает расти быстрее нагрузки. Число линий Людерса – Чернова растет, они сливаются друг с другом и теряют ясность своих очертаний. Этот участок диаграммы называется зоной упрочнения. В наивысшей точке диаграммы (в точке D) при силе равной 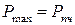 (индекс «пч» – сокращение от слова прочность) на образце внезапно появляется местное сужение – шейка, которая представляет собой результат накопления деформаций сдвига. Сопротивление образца растяжению, после образования шейки, падает, и его разрыв происходит в точке K при нагрузке
(индекс «пч» – сокращение от слова прочность) на образце внезапно появляется местное сужение – шейка, которая представляет собой результат накопления деформаций сдвига. Сопротивление образца растяжению, после образования шейки, падает, и его разрыв происходит в точке K при нагрузке 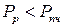 (индекс «р» – сокращение от слова разрыв).
(индекс «р» – сокращение от слова разрыв).
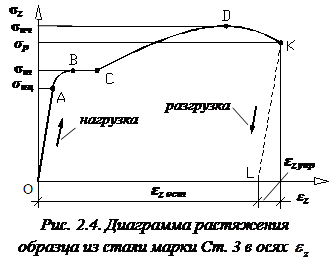
При разрыве образца, как правило, появляется поперечная трещина в центре тяжести поперечного сечения (посредине шейки), а остальная часть сечения скалывается под углом 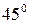 к оси образца так, что на одной части разорванного образца образуется выступ, а на другой – кратер.
к оси образца так, что на одной части разорванного образца образуется выступ, а на другой – кратер.
Линия разгрузки образца KL представляет собой прямую линию, параллельная участку ОА. Следовательно, полное удлинение образца в момент разрыва (в точке K) состоит из двух частей: упругого, исчезающего после снятия нагрузки, и остаточного, равного длине отрезка ОL.
2.14. Силы и удлинения, соответствующие характерным точкам диаграммы Бернулли, зависят не только от свойств материала, но и от размеров образца. А как определить механические характеристики материала образца?
 Для того чтобы исключить влияние абсолютных размеров образца, диаграмму, изображенную на рис. 2.3, перестраивают: ординаты делят на начальную площадь поперечного сечения
Для того чтобы исключить влияние абсолютных размеров образца, диаграмму, изображенную на рис. 2.3, перестраивают: ординаты делят на начальную площадь поперечного сечения 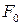 , а абсциссы – на начальную расчетную длину образца
, а абсциссы – на начальную расчетную длину образца 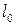 . В результате получается так называемая условная диаграмма растяжения. Она строится в координатах
. В результате получается так называемая условная диаграмма растяжения. Она строится в координатах 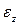 –
– 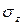 (рис. 2.4) и отличается от диаграммы Бернулли только масштабом.
(рис. 2.4) и отличается от диаграммы Бернулли только масштабом.
Условной эта диаграмма называется потому, что напряжения и деформации вычисляются по первоначальным размерам образца. Справедливость такого подхода определяется только практическими соображениями.
На условной диаграмме (см. рис. 2.4) отмечены следующие основные механические характеристики материала:
· предел пропорциональности – наибольшее напряжение, до которого выполняется закон Гука
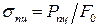 ;
;
· предел текучести – напряжение, при котором материал «течет»
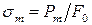 ;
;
· предел прочности– наибольшее напряжение, которое выдерживает материал без разрушения
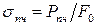 .
.
Например, для стали марки Ст. 3 упомянутые выше характеристики соответственно равны: 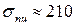 МПа,
МПа, 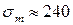 МПа,
МПа, 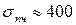 МПа.
МПа.
2.15. Для всех ли материалов диаграмма растяжения имеет вид, показанный на рис. 2.4?
Конечно же, нет. На рис. 2.4 приведенадиаграмма растяжения для стали марки Ст. 3. Этот материал относится к так называемым пластичным материалам, которые имеют площадку текучести и разрушаются при больших остаточных деформациях.
Необходимо, правда, отметить, что не для всех пластичных материалов площадка текучести имеет четко выраженный характер. Для таких материалов вводится понятие условного (или технического) предела текучести, представляющего собой напряжение, которое возникает в материале образца при относительном его удлинении, равном 0,2 %.
Иногда условный предел текучести обозначают 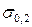 .
.
Заметим, что пластичность – это положительное свойство материала. Она играет большую роль в обеспечении надежности конструкций. Пластические свойства материала оцениваются следующими двумя характеристиками, которые также определяются при испытании на растяжение:
· относительное остаточное удлинение образца при разрыве (в процентах), вычисляемое по формуле
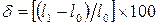 ,
,
где 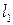 – конечная длина расчетной части образца;
– конечная длина расчетной части образца;
· относительное поперечное сужение образца при разрыве (в процентах), определяемое по формуле
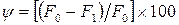 ,
,
где 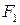 – площадь поперечного сечения образца в месте разрыва (иными словами, площадь поперечного сечения шейки).
– площадь поперечного сечения образца в месте разрыва (иными словами, площадь поперечного сечения шейки).
Однако существуют и такие материалы, например чугун, которые характерны тем, что они вообще не имеют площадки текучести. Их разрушение происходит без образования шейки. Диаграмма сжатия для них обрывается сразу же после достижения предела прочности и при очень малых остаточных деформациях. Такие материалы называют хрупкими.
2.16. В учебниках по сопротивлению материалов встречаются два понятия: «предел прочности» и «временное сопротивление разрыву». Тождественны ли они?
Не совсем. Первое из них относится к случаю, когда образец разрушается без образования шейки, что характерно для хрупких материалов. Второе относится к пластичным материалам. Временное сопротивление разрыву обозначают 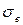 . В настоящем пособии мы не разграничиваем эти два понятия и принимаем для них общее, указанное выше, обозначение
. В настоящем пособии мы не разграничиваем эти два понятия и принимаем для них общее, указанное выше, обозначение 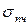 .
.
