Определить комплексные амплитуды поверхностных токов и зарядов на всех стенках трубы
Содержание
1. Техническое задание………………………………………………………………...2
2. Определение комплексных амплитуд составляющих вектора 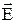 и
и 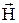 …………..4
…………..4
3. Определение диапазона частот, в котором рассматриваемое поле -
бегущая волна………………………………………………………………………...6
4. Выражения для мгновенных значений всех составляющих векторов 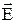 и
и 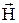 …..6
…..6
5.Расчет и построение графиков зависимостей амплитуд составляющих
векторов поля от координат x, y, z………………………………………………….....8
7. Проверка выполнения граничных условий………………………………………….16
8. Определение комплексных амплитуд плотностей поверхностных
токов и зарядов…………………………………………………………………………16
9. Определение выражений для комплексного вектора Пойнтинга. Среднее за период значение плотности потока энергии. Амплитуда плотности реактивного потока энергии…………………………………………………………………………..20
10. Вычисление среднего за период потока энергии через поперечное сечение трубы…………………………………………………………………………………….22
11. Определение фазовой скорости и скорости распространения энергии.
Расчет и построение графиков их зависимостей от частоты……………………….23
12. Определение коэффициента затухания волны…………………………………..24
13. Расчёт и построение частотной зависимости коэффициента затухания
волны в волноводе……………………………………………………………………..25
14. Определение типа волны, распространяющейся в волноводе, структура силовых линий электрического и магнитного полей этой волны, структура силовых линий плотности поверхностного тока проводимости, протекающего по стенкам волновода……………………………………………………………………………….25
15. Вывод………………………………………………………………………………..29
16. Использованная литература………………………………………………………30
Техническое задание
В полой трубе прямоугольного сечения (Рис. 1) создано монохроматическое электромагнитное поле. Труба заполнена однородной изотропной средой без потерь, абсолютная диэлектрическая и магнитная проницаемости равны 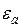 и
и 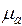 соответственно. Известно, что комплексная амплитуда вектора
соответственно. Известно, что комплексная амплитуда вектора 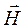 равна:
равна:
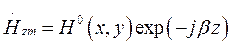 , где
, где 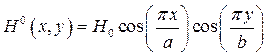 ,
, 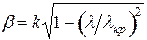 ,
, 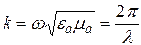 ,
, 
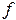 ,
, 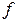 - частота электромагнитных колебаний;
- частота электромагнитных колебаний; 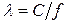 - длина волны, распространяющейся в однородной изотропной непроводящей среде с параметрами
- длина волны, распространяющейся в однородной изотропной непроводящей среде с параметрами 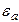 и
и 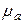 ;
; 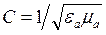 - скорость света в этой среде,
- скорость света в этой среде, 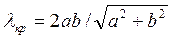 ,
, 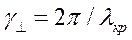
Исходные данные:
| № вар | 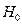 В/м В/м | 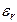 | 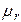 | a см | b см | 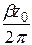 | 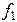 ГГц ГГц | 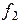 ГГц ГГц |
| 2,25 | 0,75 |
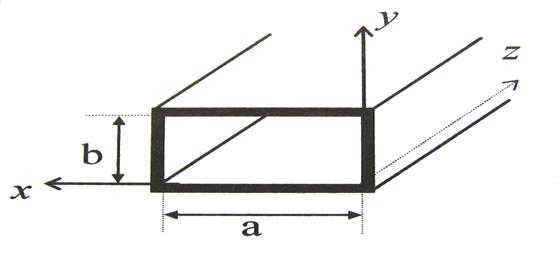

Рис. 1
Параграф № 1
Определить комплексные амплитуды поперечных составляющих вектора 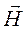 , а затем из уравнений Максвелла определить комплексные амплитуды составляющих вектора
, а затем из уравнений Максвелла определить комплексные амплитуды составляющих вектора 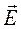 , используя соотношение
, используя соотношение
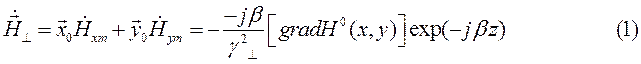 ,
,
Найдем комплексные амплитуды составляющих вектора 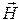 , воспользовавшись вышеприведённым соотношением:
, воспользовавшись вышеприведённым соотношением:
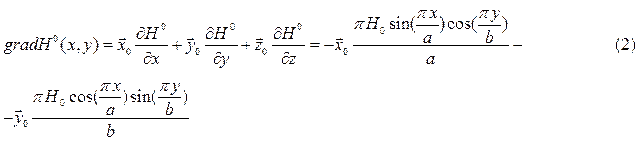
Подставляя значение из (2) в (1) найдём комплексную форму вектора 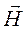 :
:
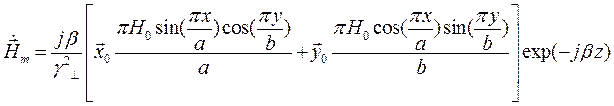
Запишем проекции комплексной амплитуды вектора 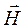 на оси координат:
на оси координат:
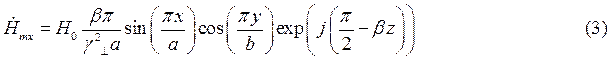
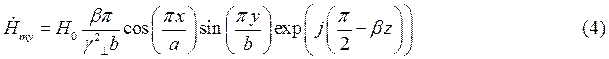
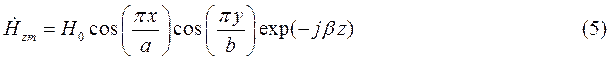
Воспользуемся вторым уравнением Максвелла в комплексной форме для определения комплексной амплитуды вектора 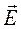 :
:
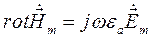 (6)
(6)
Найдем 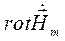 :
:
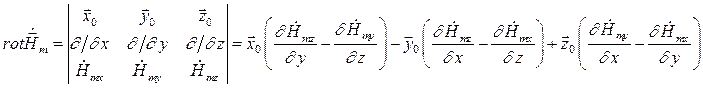
Тогда составляющие комплексной амплитуды вектора 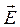 равны соответственно:
равны соответственно:
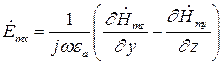 (7)
(7)
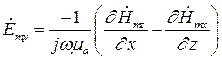 (8)
(8)
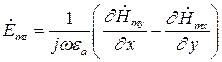
(9)
Найдем выражения для частных производных составляющих комплексной амплитуды вектора 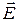 по соответствующим координатам:
по соответствующим координатам:
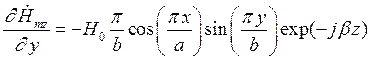
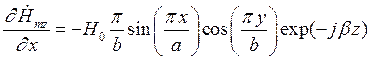
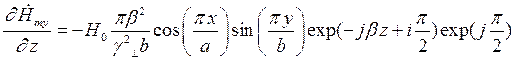
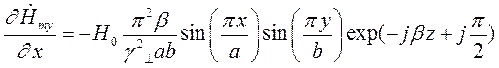
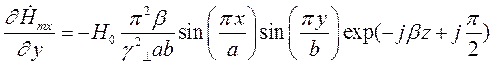
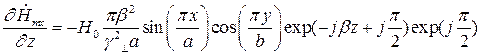
Подставляя найденные значения частных производных в (7), (8) и (9), получим итоговые выражения для комплексных амплитуд составляющих вектора 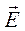 :
:
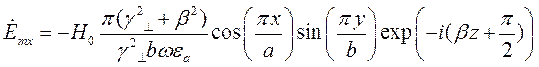 (10)
(10)
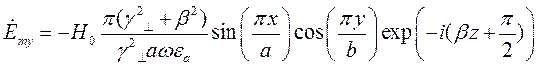 (11)
(11)
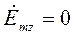 (12)
(12)
Параграф № 2
Определение диапазона частот, в котором 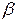 – действительное число, т.е. рассматриваемое поле – бегущая волна.
– действительное число, т.е. рассматриваемое поле – бегущая волна.
По условию задачи 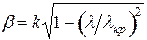 . Значит,
. Значит, 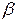 будет действительным в случае, если
будет действительным в случае, если
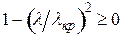 , т.е. при
, т.е. при 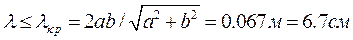
Этому диапозону длин волн соответствует диапозон частот:
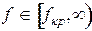 , где
, где 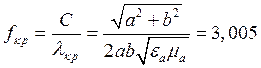 ГГц
ГГц
Таким образом, если частота волны не принадлежит рассчитанному диапазону частот, то 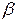 является мнимой величиной. Для этого случая произведем замену:
является мнимой величиной. Для этого случая произведем замену: 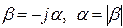 , при этом
, при этом 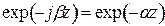 ,
, 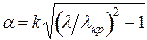
Параграф № 3
Расчёт выражения для мгновенных значений всех составляющих векторов 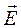 и
и 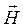 для двух случаев:
для двух случаев:
а) когда 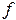 принадлежит найденному в п. 2 диапазону частот
принадлежит найденному в п. 2 диапазону частот
б) когда 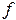 не принадлежит этому диапазону.
не принадлежит этому диапазону.
Для получения выражений для мгновенных значений составляющих векторов поля необходимо домножить их комплексные амплитуды на выражение 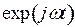 и, выделить действительную часть, то есть:
и, выделить действительную часть, то есть:
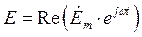 ;
; 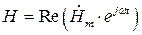
В первом случае выражения для комплексных амплитуд составляющих остаются без изменений. Во втором случае необходимо произвести замену, описанную в параграфе 2.
Для случая а) выражения для комплексны амплитуд составляющих магнитного и электрического полей имеют вид:
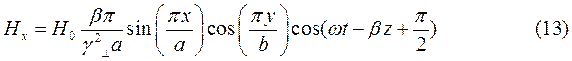
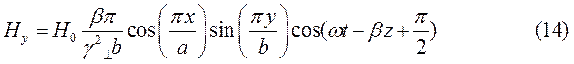
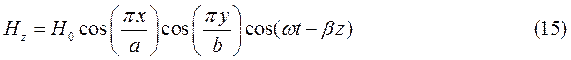
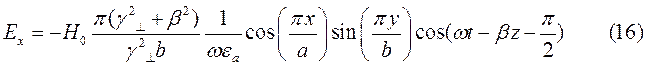
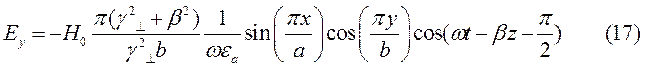
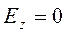 (18)
(18)
Для случая б) выражения для комплексны амплитуд составляющих магнитного и электрического полей имеют вид:
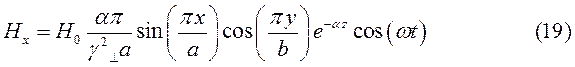
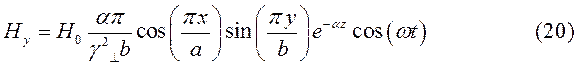
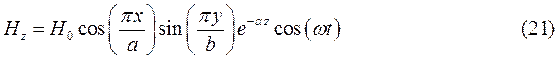
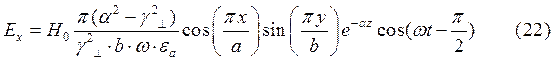
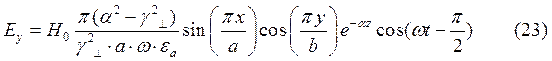
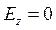 (24)
(24)
Параграф № 4
Расчёт и построение графиков амплитуд составляющих векторов поля в сечении z=z0 от координаты x при y=0,5b в интервале 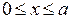 и от координаты y при x=0,75a в интервале
и от координаты y при x=0,75a в интервале 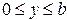 , а также зависимости тех же составляющих от координаты z вдоль линии x=0,25a; y=0,25b в интервале
, а также зависимости тех же составляющих от координаты z вдоль линии x=0,25a; y=0,25b в интервале 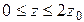 на частотах
на частотах 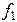 и
и 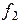 (см. таблицу).
(см. таблицу).
Для удобства, вычислим постоянные множители в математическом пакете MathCAD 14, а затем подставим соответствующие значения постоянных величин в выражения с (13) по (24):
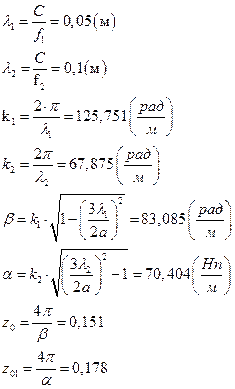 |
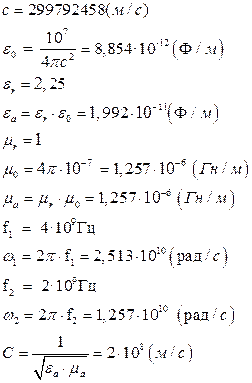
Определение амплитуд составляющих электрического и магнитного полей для Случая 1:
z=z0; y=0,5b; 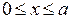 ;
; 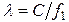
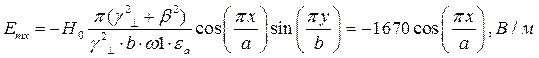
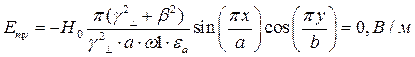
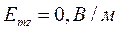
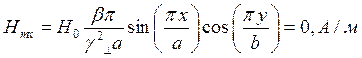
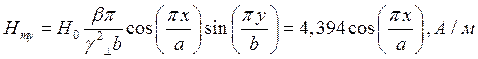
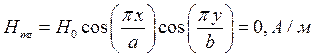
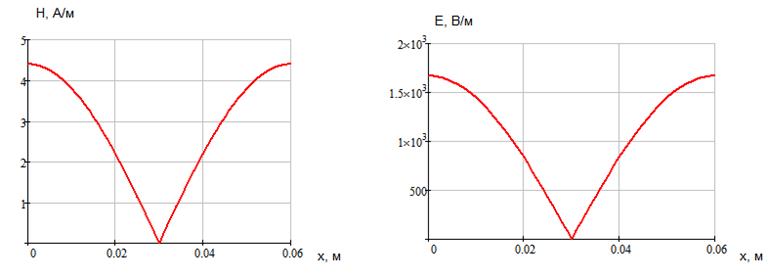
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис. 2, Рис. 3.
Определение амплитуд составляющих электрического и магнитного полей для Случая 2:
z=z0; y=0,5b; 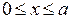 ;
; 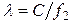
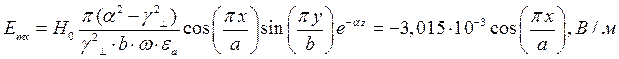
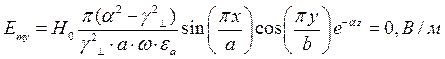
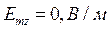
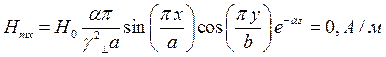
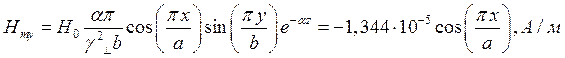
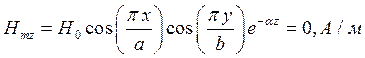
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис. 4, Рис. 5.
Определение амплитуд составляющих электрического и магнитного полей для Случая 3:
z=z0; x=0,75a; 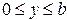 ;
; 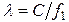
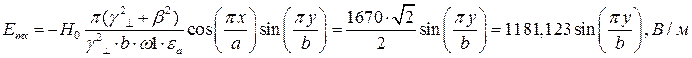
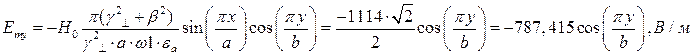
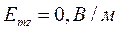
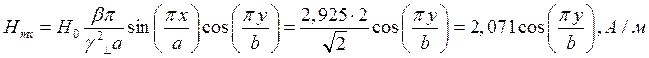
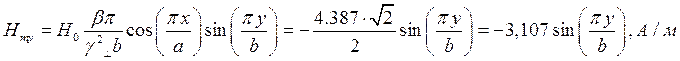
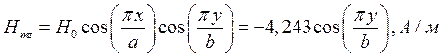
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис. 6, Рис. 7.
Определение амплитуд составляющих электрического и магнитного полей для Случая 4:
z=z0; x=0,75a; 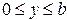 ;
; 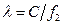
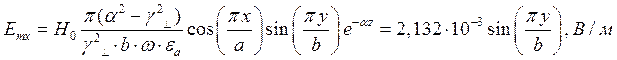
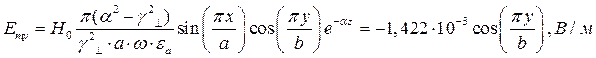
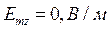
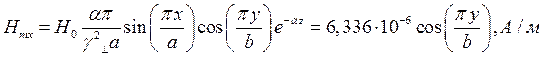
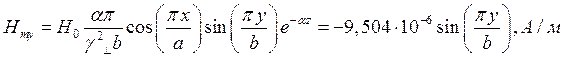
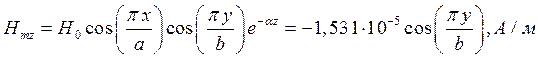
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис.8, Рис. 9.
Определение амплитуд составляющих электрического и магнитного полей для Случая 5:
x=0,25a; y=0,25b; 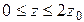 ;
; 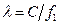
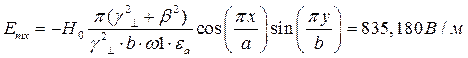
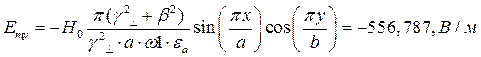
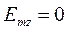
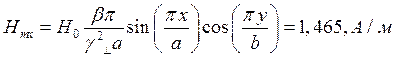
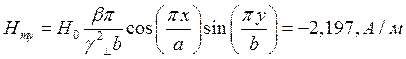
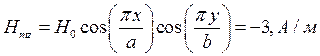
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис. 10, Рис. 11.
Определение амплитуд составляющих электрического и магнитного полей для Случая 6:
x=0,25a; y=0,25b; 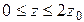 ;
; 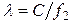
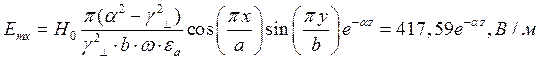
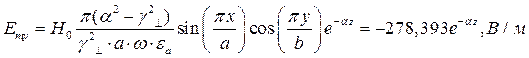
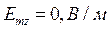
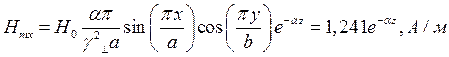
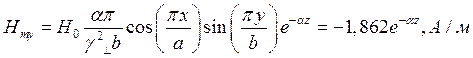
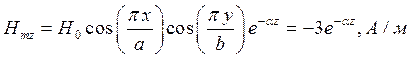
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис. 12, Рис. 13.
В выражениях для случаев 1, 3, 5 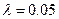 м,
м, 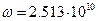 рад/с, z0=0.151 м,
рад/с, z0=0.151 м, 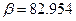 а для случаев. 2, 4, 6
а для случаев. 2, 4, 6 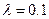 м,
м, 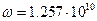 рад/с, z0=0.178 м и
рад/с, z0=0.178 м и 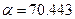 Нп/м.
Нп/м.
 ---
---
 |  | ||||||||||
 | |||||||||||
 | |||||||||||
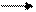 | |||||||||||
 | |||||||||||
Рис. 2 Рис. 3
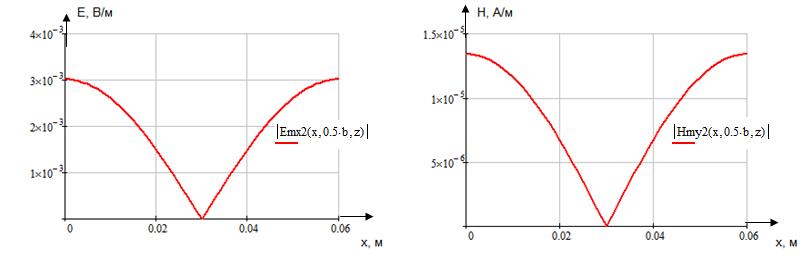
Рис. 4 Рис. 5
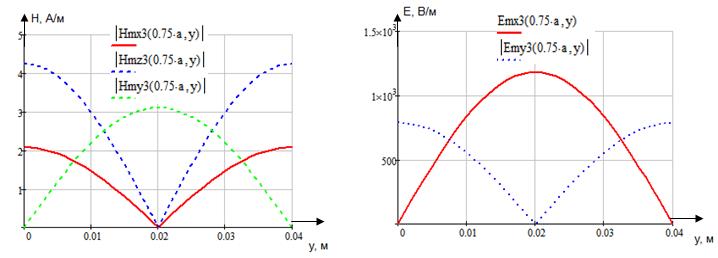
Рис. 6 Рис. 7
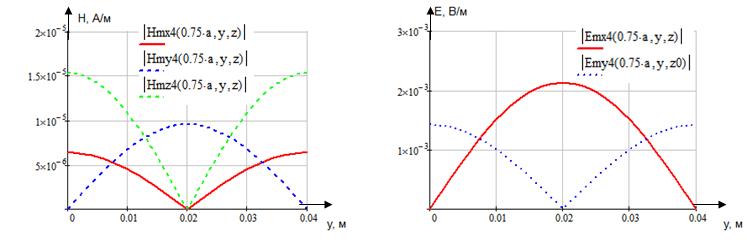
Рис. 8 Рис. 9
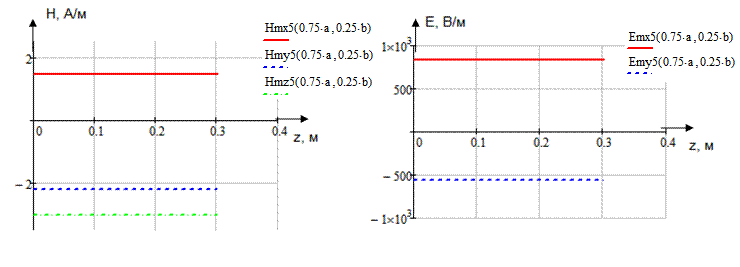
Рис. 10 Рис. 11
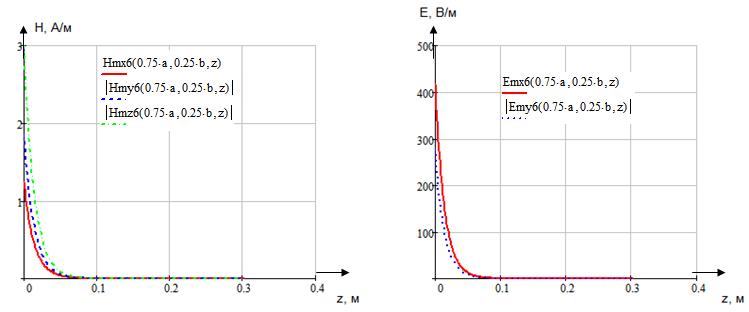
Рис. 12 Рис. 13
Параграф № 5
Проверить выполнение граничных условий для касательных составляющих вектора 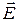 и нормальных составляющих вектора
и нормальных составляющих вектора 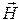 на боковой (х=а) стенке трубы.
на боковой (х=а) стенке трубы.
Проверка граничных условий заключается в проверке истинности утверждений 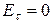 и
и 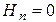 , т.е. равенста нулю касательной вектора
, т.е. равенста нулю касательной вектора 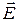 и нормальной вектора
и нормальной вектора 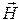 проекций (составляющих).
проекций (составляющих).
На боковой стенке (х=а) рассмотрению подлежат (17) и (13) составляющие:
Подставим в эти выражения х=а, получим:
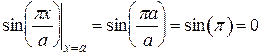 ,
,
При этом другие множители от координаты х не зависят. Следовательно, оба выражения обращаются в ноль и граничные условия выполняются.
Параграф № 6
Определить комплексные амплитуды поверхностных токов и зарядов на всех стенках трубы.
Комплексную амплитуду поверхностного тока можно найти по формуле:
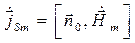
(25)
Комплексную амплитуду плотности зарядов можно найти по формуле:
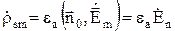 (26)
(26)
Найдем комплексные амплитуды плотностей поверхностных токов и зарядов на всех стенках трубы:
1) Для нижней стенки трубы 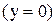 нормаль совпадает с вектором
нормаль совпадает с вектором 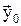 :
: 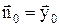 .
.
Касательными к этой стенке составляющими вектора 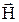 являются составляющие вдоль осей x и z, то есть:
являются составляющие вдоль осей x и z, то есть:
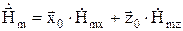
Подставим это выражение в формулу (25):
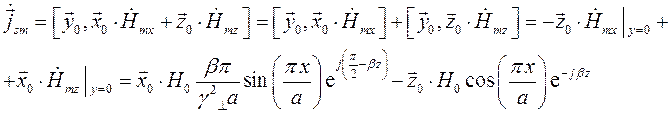
Нормальной к этой стенке составляющей вектора 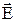 будет составляющая
будет составляющая 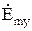 . Тогда комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
. Тогда комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
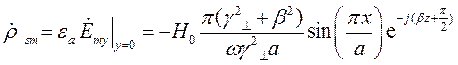
2) Для верхней стенки трубы 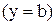 нормаль противоположна вектору
нормаль противоположна вектору 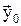 :
: 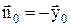 .
.
Касательными к этой стенке составляющими вектора 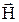 являются составляющие вдоль осей x и z, то есть:
являются составляющие вдоль осей x и z, то есть:
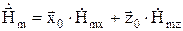
Подставим это выражение в формулу (25):
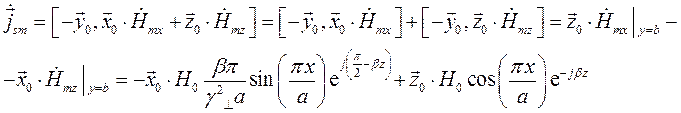
Нормальной к этой стенке составляющей вектора 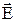 будет составляющая
будет составляющая 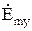 . Комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
. Комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
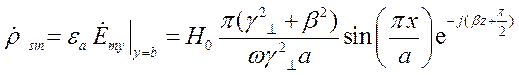
3) Для правой стенки трубы 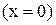 нормаль совпадает с вектором
нормаль совпадает с вектором 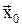 :
: 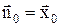 .
.
Касательными к этой стенке составляющими вектора 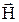 являются составляющие вдоль осей y и z, то есть:
являются составляющие вдоль осей y и z, то есть:
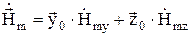
Подставим это выражение в формулу (25):
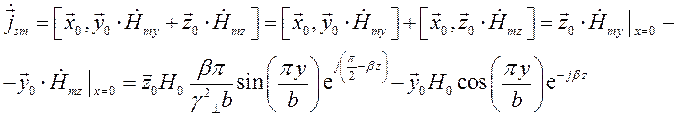
Нормальной к этой стенке составляющей вектора 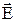 будет составляющая
будет составляющая 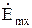 . Комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
. Комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
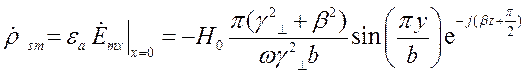
4) Для левой стенки трубы 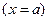 нормаль противоположна вектору
нормаль противоположна вектору 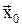 :
: 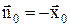 .
.
Касательными к этой стенке составляющими вектора 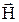 , как и в третьем случае, являются составляющие вдоль осей y и z, то есть:
, как и в третьем случае, являются составляющие вдоль осей y и z, то есть:
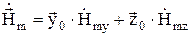
Подставим это выражение в формулу (25):
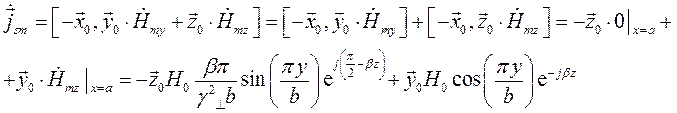
Нормальной к этой стенке составляющей вектора 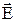 будет составляющая
будет составляющая 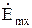 . Комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
. Комплексная амплитуда плотности поверхностных зарядов по формуле (26) будет равна:
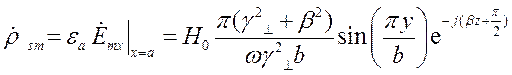
Комплексные амплитуды поверхностных токов и зарядов на всех стенках трубы показаны на Рис. 14, Рис. 15, Рис. 16. Рис. 17
Нижняя стенка (y = 0) Рис. 14
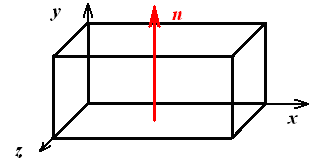
Верхняя стенка (y = b) Рис. 15
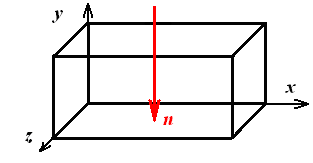
Правая стенка (x =0) Рис. 15
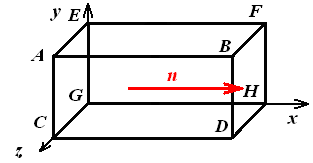
Левая стенка (x =a) Рис. 16
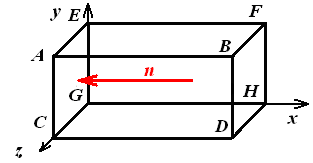
Параграф № 8
Записать выражение для комплексного вектора Пойтинга для двух случаев: когда частота принадлежит найденному в п. 2 диапазону и когда она не принадлежит этому диапазону. Определить среднее за период значение плотности потока энергии и амплитуду плотности реактивного потока энергии.
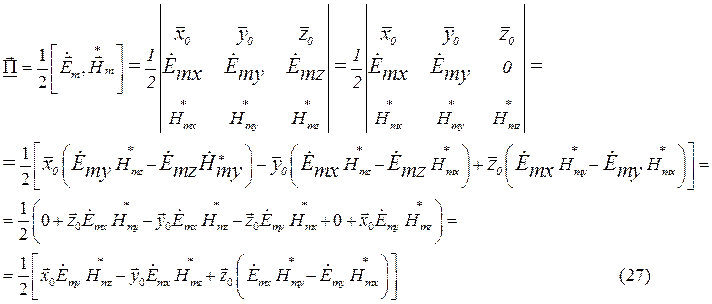
Рассмотрим режим бегущей волны 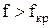 :
:
Запишем выражения для сопряженных составляющих вектора 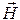 :
:
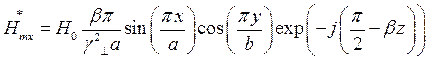
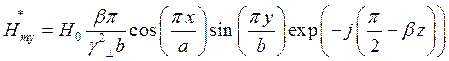
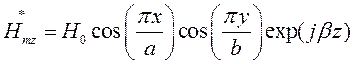
Найдём выражения для каждой из составляющих вектора Пойтинга, исходя из (27):
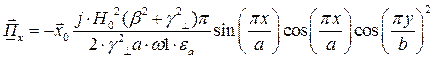
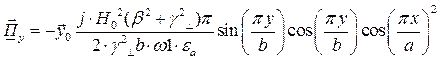
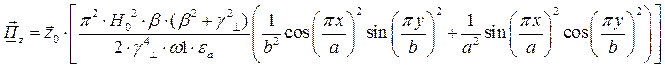
Тогда выражение для вектора Пойтинга примет вид:
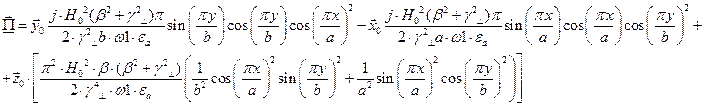
Cоставляющие по оси х и по оси у чисто мнимые, а составляющая по оси z – действительная, значит вдоль оси z происходит перенос энергии. Следовательно:
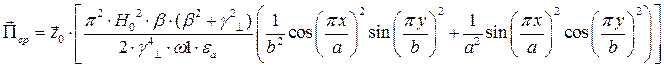
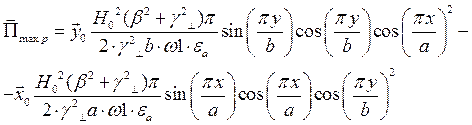
Рассмотрим режим стоячей волны 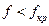 :
:
Запишем выражения для сопряженных составляющих вектора 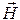 :
:
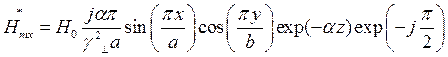
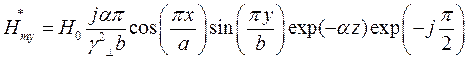
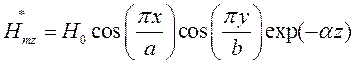
Найдём выражения для каждой из составляющих вектора Пойтинга, исходя из (27):
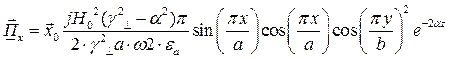
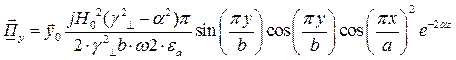
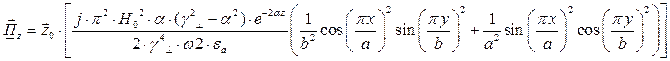
В этом случае вектор Пойтинга чисто мнимый и переноса энергии не происходит.
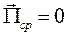
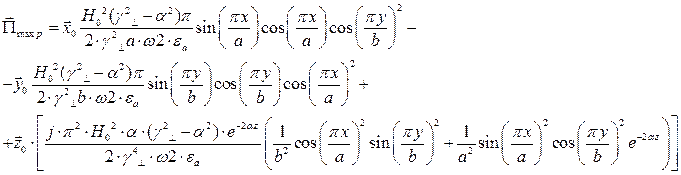
Параграф № 10
