Ряд геометрической прогрессии
Рассмотрим бесконечную геометрическую прогрессию с общим членом: 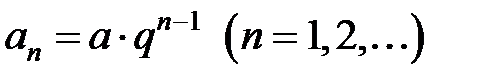 и соответствующий числовой ряд:
и соответствующий числовой ряд:
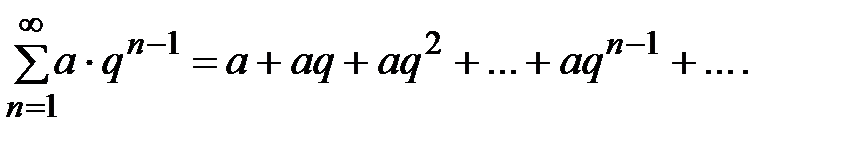 (13.8)
(13.8)
Частичная сумма такого ряда имеет вид:
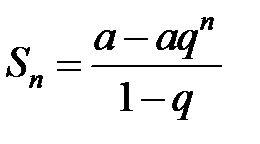 . (13.9)
. (13.9)
Возьмем предел этого соотношения:
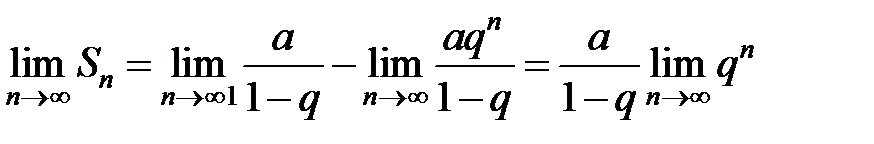 .
.
В зависимости от числового значения знаменателя прогрессии частичная сумма 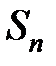 при
при 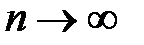 будет сходящейся или расходящейся.
будет сходящейся или расходящейся.
Рассмотрим возможные случаи:
1) 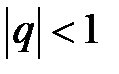 . Предел частичной суммы ряды при
. Предел частичной суммы ряды при 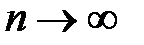 существует, то есть:
существует, то есть:
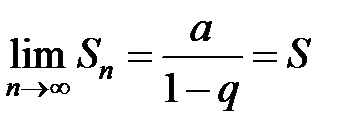 , так как
, так как 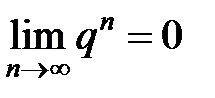 .
.
Следовательно ряд, построенный из членов бесконечно убывающей геометрической прогрессии сходится;
2) 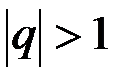 . Предел частичной суммы ряда при
. Предел частичной суммы ряда при 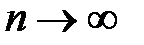 бесконечный, то есть:
бесконечный, то есть: 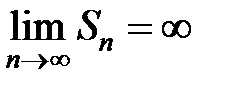 , так как
, так как 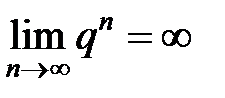 . Следовательно, ряд расходится;
. Следовательно, ряд расходится;
3) 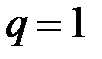 . В этом случае частичная сумма ряда может быть вычислена таким образом:
. В этом случае частичная сумма ряда может быть вычислена таким образом:  .
.
Следовательно, 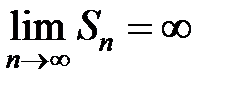 , то есть ряд расходится;
, то есть ряд расходится;
4) 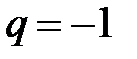 . Частичную сумму ряда можно вычислить таким образом:
. Частичную сумму ряда можно вычислить таким образом:
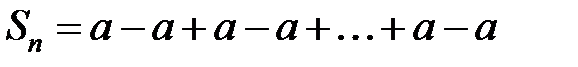 .
.
Следовательно, 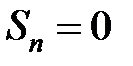 , если
, если 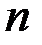 – четное,
– четное, 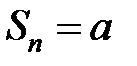 , если
, если 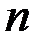 – нечетное. То есть
– нечетное. То есть 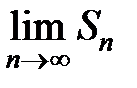 не существует, а это значит, что ряд расходится.
не существует, а это значит, что ряд расходится.
Итак, ряд сходится при 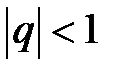 и расходится при
и расходится при 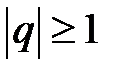 .
.
Гармонический ряд
Исследуем сходимость ряда с общим членом:
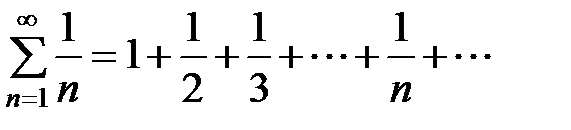 . (13.10)
. (13.10)
Этот ряд называется гармоническим. Запишем этот ряд более детально:
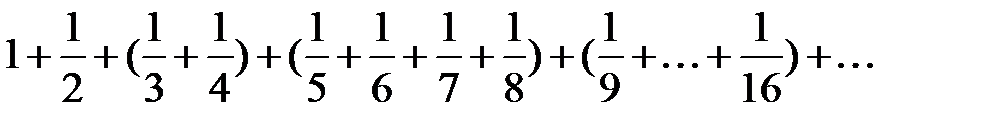 .
.
Сравним данный ряд с рядом вида:
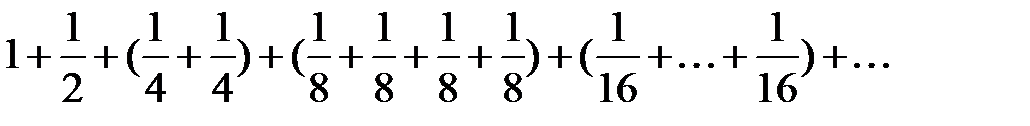 .
.
Для всех 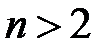 имеет место соотношение:
имеет место соотношение: 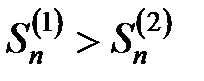 .
.
Вычислим 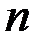 -ю частичную сумму, где
-ю частичную сумму, где 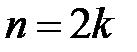 (
( 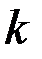 – число скобок в частичной сумме) вспомогательного ряда:
– число скобок в частичной сумме) вспомогательного ряда: 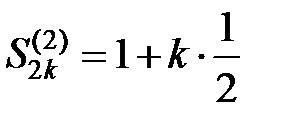 .
.
Если 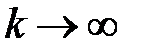 , то
, то 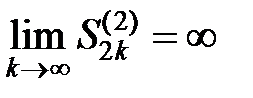 . То есть ряд расходится.
. То есть ряд расходится.
Так как 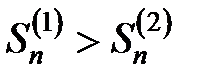 , то
, то 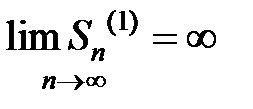 . Следовательно, гармонический ряд (22.10) является рядом расходящимся.
. Следовательно, гармонический ряд (22.10) является рядом расходящимся.
Ряд, который получен из данного отбрасыванием первых 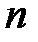 членов
членов
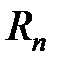 =
= 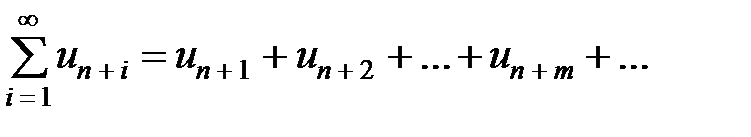 , (13.11)
, (13.11)
называется 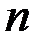 -м остатком ряда.
-м остатком ряда.
У остатка первым членом является 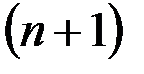 член исходного ряда.
член исходного ряда.
Теорема 1.Если ряд (13.1) сходится, то сходится и его остаток и, наоборот, если сходится остаток ряда, то сходится и данный ряд.
Следствие. Сходимость или расходимость ряда не нарушается, если изъять из него или прибавить к этому ряду конечное число членов.
Теорема 2.Если ряд сходится, то сходится и ряд, который получен из данного умножением на постоянное число.
Теорема 3. Если ряды с общими членами 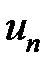 и
и 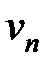 сходящиеся и
сходящиеся и
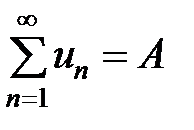 , а
, а 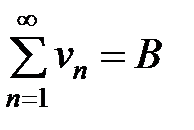 ,
,
то для любых чисел 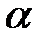 и
и 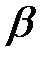 ряд с общим членом:
ряд с общим членом: 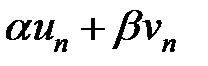 сходится, а его сумма равна:
сходится, а его сумма равна: 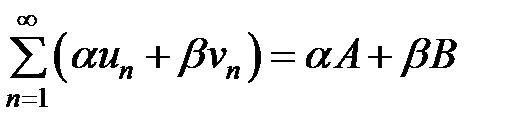 .
.
Теорема(необходимый признак сходимости). Если ряд 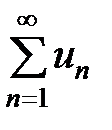 сходится, то предел общего члена ряда при
сходится, то предел общего члена ряда при 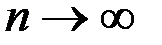 равен 0, то есть:
равен 0, то есть:
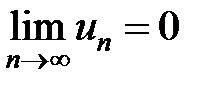 .
.
Нужно иметь в виду, что когда необходимое условие не выполняется, то исследуемый ряд является расходящимся.
То есть условие 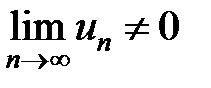 является достаточным признаком расходимости числового ряда. Если необходимый признак выполняется, то это не значит, что соответствующий ряд сходится. То есть вопрос остается открытым и нуждается в дальнейшем исследовании.
является достаточным признаком расходимости числового ряда. Если необходимый признак выполняется, то это не значит, что соответствующий ряд сходится. То есть вопрос остается открытым и нуждается в дальнейшем исследовании.
Пример 6.Исследовать на сходимость ряды:
а) 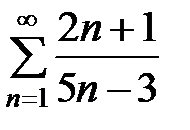 .
.
Решение.
Найдем предел общего члена ряда: 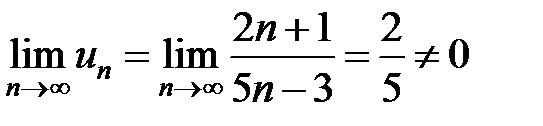 ,
,
то есть необходимый признак не выполняется и ряд расходится;
б) 
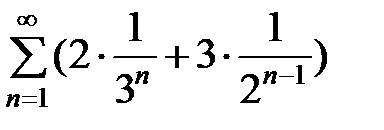 .
.
Решение.
Общий член этого ряда имеет вид: 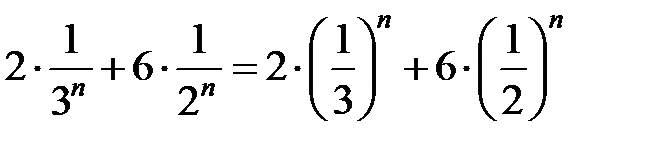 .
.
Рассмотрим вспомогательные ряды: 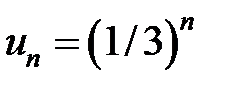 и
и 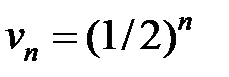 . Каждый из этих рядов с общими членами
. Каждый из этих рядов с общими членами 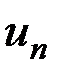 и
и 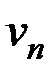 сходится, поскольку эти ряды образуются бесконечными убывающими геометрическими прогрессиями (13.8).
сходится, поскольку эти ряды образуются бесконечными убывающими геометрическими прогрессиями (13.8).
В результате применения теоремы 3 исследуемый ряд сходится и его сумма равна сумме первого и второго вспомогательных рядов.
