Ряд геометрической прогрессии.

Так называется ряд (бесконечная сумма), члены которого образуют геометрическую прогрессию с первым членом а₀ и знаменателем прогрессии, равным q.

Если |q| < 1, то существует предел суммы n первых членов этой прогрессии при неограниченном увеличении количества этих членов n:

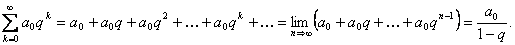
В этом случае говорят о бесконечно убывающей геометрической прогрессии

Остаток числового ряда. Необходимый признак сходимости числового ряда.

Ряд, полученный отбрасыванием от исходного n первых членов называется n-м остатком ряда. Обозначение:

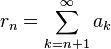
Для остатка ряда справедливы следующие утверждения:

1. Если ряд сходится, то сходится любой его остаток.

2. Если хотя бы один остаток ряда сходится, то и сам ряд сходится.

3. Если ряд сходится, то

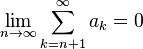
Существуют способы оценки остатка ряда с помощью интегрального признака Коши (для знакоположительного ряда) и Признака сходимости Лейбница (для знакочередующегося ряда).

Гармонический ряд.

Гармонический ряд –числовой ряд
.
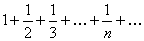Члены этого ряда обратны соответствующим натуральным числам.

Как установил в 1673 г. Г. Лейбниц, этот ряд расходится, т.е. частичные суммы ряда, 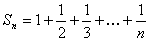, неограниченно растут при неограниченном росте количества n членов сумм. Гармонический ряд обычно приводят как пример того, что стремление к нулю n-го члена ряда при неограниченном росте его номера еще не обеспечивает его сходимость, это лишь необходимый, а не достаточный признак сходимости.

Свое название гармонический ряд, возможно, получил из-за такого очевидного свойства: каждый его член, начиная со второго, есть среднее гармоническое двух своих соседей – предыдущего и последующего членов.

Среднее гармоническое n положительных чисел, a₁, a₂, …, a_n равно 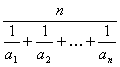(здесь n ≥ 2).

Основные свойства сходящихся рядов. Критерий сходимости рядов с положительными членами.

(29. 2.) Запишем три свойства, определяющие сходимости числовых рядов, первое из которых связано с отбрасыванием конечного числа членов.

1?. Сходимость ч.р. не зависит от отбрасывания конечного числа членов.

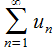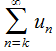Разберем и . Предположим, что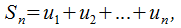

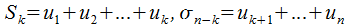, в этом случае

(29.1)

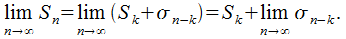
При наличии конечного предела справа в (29.1) можно заключить, что существует и предел слева, и ряд 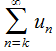предполагает сходимость.

2?. При условии, что ряд 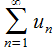сходится и его сумма составляет 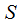можно заключить, что ряд 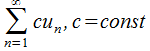, сходится и имеет сумму .

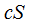Допустим, что 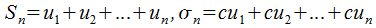, таким образом

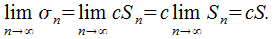
3. При условии, что 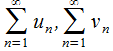сходятся и имеют суммы 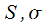, соответствено, можно заключить, что 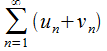сходится и имеет сумму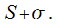

Предположим, что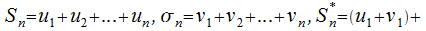

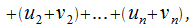в этом случае

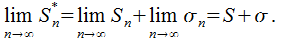
Признаки сравнения рядов.

Теорема(признак сравнения). Пусть даны два ряда с положительными членами

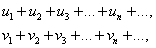
причём члены первого ряда не превосходят соответствующих членов второго, т.е.

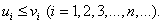(18)

Тогда из сходимости второго ряда следует сходимость первого, а из расходимости первого ряда – расходимость второго.

Замечание. Условие (18) не обязательно должно выполняться с первых членов рядов и только для членов с одинаковыми номерами. Достаточно, чтобы оно выполнялось начиная с некоторого номера kили чтобы имели место неравенства

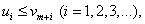
где m – некоторое целое число.