Электромагнитные волны в среде

С ПРОВОДИМОСТЬЮ

3.6.1. Комплексная диэлектрическая проницаемость

1. Реальная среда в той или иной степени обладает проводимостью, т.к. в любой реальной среде содержится некоторое количество свободных зарядов. По проводимости среды делятся на проводники, полупроводники и диэлектрики. Вспомним курс общей физики. Энергетический спектр электронов в кристаллах имеет зонную структуру, и с позиции зонной теории проводимость сред количественно оценивается по энергетической ширине De последней запрещенной зоны (запрещенная зона находится между валентной зоной и зоной проводимости). Валентные электроны могут покидать свои атомы, если электроны приобретут достаточную энергию для преодоления потенциального барьера запрещенной зоны, и «принять участие» в электрическом токе.

В проводниках (например, в металлах) валентная зона и зона проводимости перекрываются, и валентные электроны в металлах уже при температурах близких к 0 К находятся в зоне проводимости. Металлы являются хорошими проводниками. Условно принято, что полупроводниками являются материалы, у которых ширина последней запрещенной зоны De < 2 эВ. Например, ширина запрещенной зоны известных полупроводниковых кристаллов кремния Si и германия Ge De » 1 эВ. К диэлектрикам (диэлектрики называют еще изоляторами) относятся материалы, ширина последней запрещенной зоны которых De > 2 эВ. Однако, несмотря на довольно большую энергетическую ширину последней запрещенной зоны диэлектриков, статистически в межатомном пространстве реальных диэлектриков все же содержится некоторое количество свободных электронов, поэтому и диэлектрики обладают проводимостью, хотя и незначительной. Итак, соотношение между проводимостями диэлектриков g_д., полупроводников g_пп. и проводников g_пр можно выразить неравенством:

g_д.<< g_пп < g_пр.,

(напомним, g = 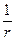, где r – удельное сопротивление среды).

2. Классификация сред на проводники и диэлектрики с позиции электродинамики определяется по относительному значению тока проводимости j= gEи тока смещения j_см. = 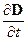= 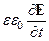. Ток проводимости gE обусловленным движением свободных зарядов, ток смещения 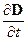обусловленным переменным электромагнитным полем. Если в среде ïgEï>>ï 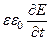ï, то такая среда является проводником, если ïgEï<<ï 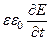ï, то среда является диэлектриком. При условии, когда ïgEï и ï 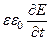ïодного порядка, то такую среду будем называть полупроводником.

Важно в приведенных оценочных неравенствах обратить внимание на то обстоятельство, что соотношение между током проводимости j и током смещения j_см зависит не только от параметров среды g и e, но и от быстроты изменения электрического поля электромагнитной волны - зависит также и от значения 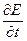, т.е. от частоты колебаний вектора E.

Допустим, электромагнитная волна является синусоидальной. Запишем уравнение Максвелла для ротора комплексной амплитуды H (раздел 3.4):

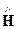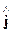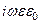
[Ñ,] = + 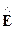или [Ñ,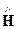] = (g + ).

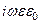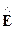Последнее уравнение можно представить в виде:

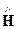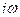
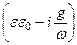
[Ñ,] = 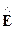. (70)

Комплексная величина:

e_к = 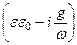(71)

называется комплексной диэлектрической проницаемостью.

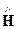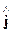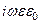
Итак, вместо уравнения [Ñ,] = + 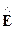будем иметь уравнение

[Ñ,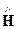] = 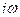e_к 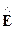. (72)

Уравнение (72) позволяет рассматривать любую среду как диэлектрик с комплексной диэлектрической проницаемостью e_к. Соотношение между вещественной частью ee₀ и мнимой 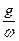комплексной диэлектрической проницаемости e_к определяет свойства среды:

- при g >> ee₀w среда является проводником;

- при g << ee₀w среда является реальным диэлектриком.

При граничной частоте w_гр. = 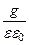(73)

амплитуды тока проводимости и тока смещения равны. При высоких частотах электромагнитной волны (w >> w_гр.) основную роль играют токи смещения, и среда при этих частотах рассматривается как диэлектрик; при низких частотах волны (w << w_гр.) основную роль играют токи проводимости, и среда при этих частотах рассматривается как проводник.

Например, проводимость меди g = 5,7×10⁷ Сим/м, диэлектрическая проницаемость металлов того же порядка, что и диэлектрическая проницаемость воздуха e ~ (1 ¸ 10). Если принять e = 10, то имеем:

f_гр. = 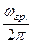= = 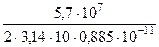10¹⁷ Гц.

Полученная частота находится в ультрафиолетовом диапазоне электромагнитных волн (длина волны 3×10^-9м). В радиодиапазоне (радиодиапазон простирается до частот 10¹³¸10¹⁴ Гц) металлы являются проводниками. Таким образом, в металлах в радиодиапазоне частот ток проводимости превышает ток смещения более чем в 10³ раз. Для пресной воды (g = 10^-3 Сим/м, e = 81) граничная частота f_гр. = 2×10⁵ Гц; для морской соляной воды (g = 4 Сим/м, e = 81) f_гр. = 10⁹ Гц.

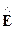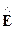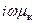
В нелинейных магнетиках (например, в ферромагнетиках) возможны магнитные потери и магнитная проницаемость становится комплексной величиной m_к, и уравнение для ротора вектора комплексной амплитуды запишется в виде: [Ñ,] = 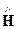. (74)

В дальнейшем будем рассматривать линейные магнетики с постоянной магнитной проницаемостью и в отсутствии магнитных потерь в среде.

Умножив (72) и (74) на 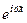, получим уравнения Максвелла для роторов комплексных функцийE_к и H_к в среде с проводимостью:

[Ñ, H_к] = 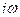e_к E_к, (75)

[Ñ, E_к] = 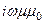H_к, (76)

а также уравнения для дивергенций:

Ñ H_к = 0 и Ñ E_к = 0. (77)

3.6.2. Уравнение плоской волны в среде с проводимостью

Прежде чем рассматривать содержание данного параграфа, рекомендуем еще раз перечитать раздел 3.5, где приводятся волновые уравнения вещественных векторов E и H в идеальном диэлектрике и решения этих уравнений.

В идеальном диэлектрике волновое уравнение (40) получено из анализа уравнений Максвелла (26). Решением волновых уравнений являются уравнения волны (44*) и (45*), которые представим в комплексной форме, выделив отдельно множитель 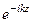, зависящий от координаты:

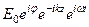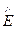
E_к = = 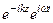; (78)

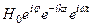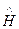
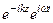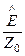
H_к = = = 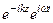, (79)

где Z₀ = 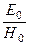= 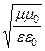, k = 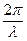= 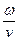. Так как фазовая скорость волны в диэлектрике определяется выражением v = 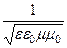, то волновое число можно записать в виде k = 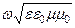. Уравнения (78) и (79) описывают электромагнитную волну, распространяющуюся в положительном направлении оси 0Z, на это указывает знак минус в сомножителе .

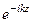Среда с проводимостью. Структура уравнений Максвелла для комплексных функцийE_к и H_к в среде с проводимостью (75, 76, 77) одинакова со структурой системы уравнений Максвелла (26) в идеальном диэлектрике. Следовательно, решенияE_к и H_к в среде с проводимостью будут иметь вид, аналогичный уравнениям (78) и (79) с учетом того, что в среде с проводимостью диэлектрическая проницаемость e_к – комплексная величина. В решении волнового уравнения для среды с проводимостью вещественное волновое число k (вещественный фазовый множитель) следует заменить комплексной величиной 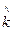- комплексным фазовым множителем, а вещественное волновое сопротивление Z₀ заменить комплексным волновым сопротивлением :

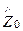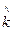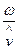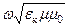= = , где 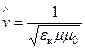- комплексная фазовая скорость;

= = .

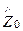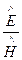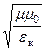Запишем уравнения волны комплексных функцийнапряженности электрического поля E_к и напряженности магнитного поля H_к в среде с проводимостью E_к =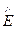 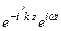; (80)

H_к = 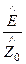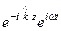, (81)

Проведем анализ уравнений (80) и (81).

1. Комплексная величина 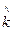, как любая комплексная величина, может быть представлена в виде:

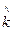= k - ia (82)

Подставим (82) в (80), получим:

E_к =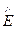 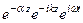. (83)

Пусть начальная фазаEравна нулю, тогда это уравнение в тригонометрической форме имеет вид:

E_x = E₀ 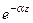cos (wt - kz) (83*)

(напомним, в этой записи принято, что плоская волна распространяется в положительном направлении оси 0Z, вектор E колеблется по оси 0X, вектор H - по оси 0Y).

Из (83) следует, что положительная величина a (мнимая часть комплексного фазового множителя 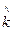) определяет затухание амплитуды волны с расстоянием по мере удаления электромагнитной волны от источника волны и называется коэффициентом затухания. В экспериментальном плане a равна обратной величине некоторого расстояния l₀, на котором амплитуда волны E₀ 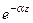уменьшается в e » 2,7 раз: a = 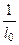. Ясно, что механизм потерь электромагнитной энергии в проводящей среде обусловлен возбуждением в среде электрических токов с последующим выделением джоулевого тепла.

Величина k имеет тот же смысл волнового числа, что и в уравнении волны в идеальном диэлектрике: k = 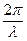. Как и в идеальном диэлектрике, в среде с проводимостью волновое число k определяет фазовую скорость волны: v = 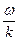. Фазовая скорость – это скорость распространения волновой поверхности (например, передней волновой поверхности - фронта волны).

2. Комплексное волновое число представим в форме Эйлера (через экспоненту): 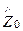=Z₀ 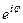. Здесь Z₀ - модуль, j - аргумент волнового сопротивления. Тогда уравнение волны для комплексной функции напряженности магнитного поля запишется как:

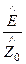
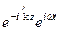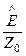
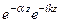
H_к = = 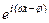. (84)

В обычной тригонометрической записи уравнение волны для напряженности магнитного поля электромагнитной волны в среде с проводимостью примет вид: H_y = 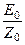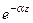cos (wt - kz - j). (85)

Из сравнения уравнений (83) и (85) следует, что в среде с проводимостью имеется сдвиг фаз между электрическим и магнитным полями электромагнитной волны. Напомним, в идеальном диэлектрике фазовый сдвиг между векторами E и H отсутствует (§3.5.2).

Воспользовавшись соотношениями для комплексного фазового множителя и комплексного волнового сопротивления

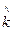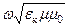= = k - ia и 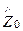= = 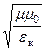Z₀ 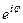, где e_к = ,

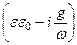можно получить оценочные формулы для вещественных величин: коэффициента затухания a; вещественного фазового множителя k; фазовой скорости v; модуля аргумента волнового сопротивления Z₀; сдвига фаз j между E и H. Вывод основывается на возведение в квадрат первого соотношения и последующего приравнивания действительной и мнимой частей полученного равенства. Вывод оценочных формул несложный, и подробности вывода здесь опустим. Приведем результаты для двух случаев.

А. Среда - реальный диэлектрик (ee₀w >> g - среда обладает незначительной проводимостью):

- волновое сопротивление: Z₀ = »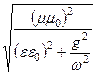

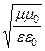
- коэффициент затухания: a² = wee₀mm₀ 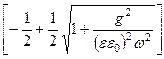» 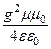или

a » = ;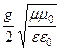

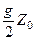- фазовой множитель: k = wee₀mm₀ » ;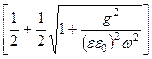

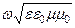- фазовая скорость волны: v = = » ;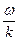

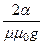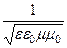- сдвиг фазы между E и H: j = arctg 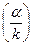» 0.

Из приведенных оценок следует, что в реальном диэлектрике с незначительной проводимостью результаты такие же, что и в идеальном диэлектрике. В реальном диэлектрике коэффициент затухания a не зависит от частоты, а определяется проводимостью g и волновым сопротивлением Z₀.

Б. Среда - проводник. С учетом соотношения для хорошо проводящей среды g >> ee₀w , получим:

- волновое сопротивление: Z₀ » ;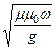

- коэффициент затухания: a » ;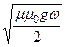

- фазовой множитель: k » ;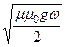

- фазовая скорость волны: v » ;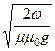

- сдвиг фазы между E и H: j = arctg » .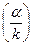

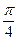Из полученных оценок следует, что в проводящей среде:

1) происходит поглощение энергии электромагнитной волны, и это поглощение можно характеризовать коэффициентом затухания амплитуды волны в проводящей среде, причем в проводниках a » k (напомним, в курсе общей физики было показано, что энергия электромагнитной волны определяется квадратом амплитудыE и H). Например, в меди при обычной радиотехнической частоте f = 100 МГц (длина волны 3 м) a » 15×10⁴ м^-1 , следовательно, при прохождении волной расстояния l₀ = 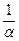» 7×10^-6 м = 7×10^-3мм амплитуда в проводящей среде уменьшается в e = 2,7 раз;

2) фазовая скорость v очень мала. Например, в меди v » 4×10² м/с (сравните, в вакууме v » 3×10⁸ м/с);

3) волновое сопротивление Z₀ проводников очень мало. Например, волновое сопротивление меди » 4×10^-3 Ом (сравните, волновое сопротивление вакуума » 380 Ом). Уже из этого следует, что в проводящей среде перенос энергии осуществляется в основном магнитным полем электромагнитной волны (см. определение волнового сопротивления). Приведем оценку данного эффекта, для чего сравним максимальную плотность энергии магнитного и электрического поля электромагнитной волны в проводящей среде:

= = = .

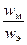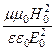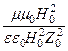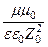Например, для меди 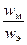» 3×10⁷, т.е. практически вся энергия электромагнитного поля в проводнике сосредоточена в магнитном поле (при вычислении принято, что магнитная проницаемость m и диэлектрическая проницаемость порядка металлов порядка проницаемости воздуха, т.е. ~ 1);

4) в проводниках фазы колебаний векторов E и Hне совпадают.