Апериодическое (инерционное) звено второго порядка

ВОПРОС 21 Типовые динамические звенья их основные характеристики

Типовые динамические звенья - это минимально необходимый набор звеньев для описания системы управления произвольного вида. Типы звеньев систем управления различаются по виду их передаточной функции (или дифференциального уравнения), определяющей все их динамические свойства и характеристики. Классификация основных типов динамических звеньев приведена на рис.3.9.

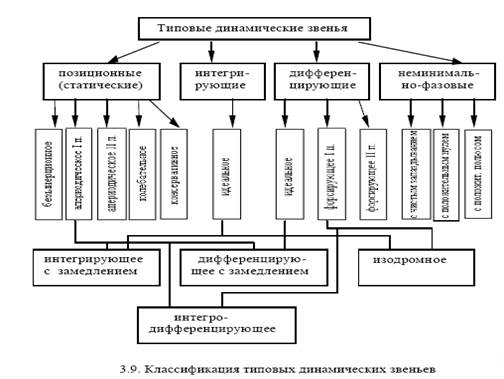
Основные типы звеньев делятся на четыре группы: позиционные, интегрирующие, дифференцирующие и неминимально-фазовые. Позиционные, интегрирующие и дифференцирующие звенья относятся к минимально-фазовым. Важным свойством минимально-фазовых звеньев является однозначное соответствие амплитудной и фазовой частотных характеристик. Другими словами, по заданной амплитудной характеристике всегда можно определить фазовую и наоборот.

Позиционные звенья

В звеньях позиционного, или статического типа, линейной зависимостью y = kx связаны выходная и входная величины в установившемся режиме. Коэффициент пропорциональности k между выходной и входной величинами представляет собой

коэффициент передачи звена. Позиционные звенья обладают свойством самовыравнивания, то есть способностью самостоятельно переходить в новое установившееся состояние при ограниченном изменении входного воздействия.

Безынерционное (идеальное усилительное) звено.

Это звено не только в статике, но и в динамике описывается алгебраическим уравнением y(t) = kx(t). (3.14)

Передаточная функция:

W(s) = k. (3.15)

Амплитудно-фазовая частотная характеристика:

W(jω) = k, A(ω) = k, ψ(ω) = 0. (3.16)

Переходная и импульсная функции:

h(t) = k1(t), w(t) = kδ(t). (3.17)

Безынерционное звено является некоторой идеализацией реальных звеньев. В ействительности ни одно звено не в состоянии равномерно пропускать все частоты от 0 до ∞.

Примерами таких безынерционных звеньев могут служить жесткая механическая передача, часовой редуктор, электронный усилитель сигналов на низких частотах и др.

Апериодическое (инерционное) звено первого порядка.

Уравнение и передаточная функция звена:

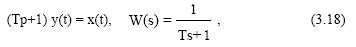
где T - постоянная времени, характеризует степень инерционности звена, т.е. длительность переходного процесса.

Амплитудно-фазовая частотная характеристика:

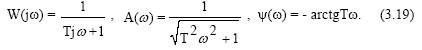
Таким образом, апериодическое звено первого порядка является фильтром низких частот.

Переходная и импульсная функции:

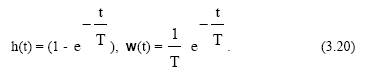
Примерами апериодического звена первого порядка могут служить RC цепочка, нагревательный элемент и др.

Апериодическое (инерционное) звено второго порядка.

Дифференциальное уравнение звена имеет вид

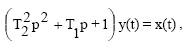
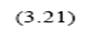
причем предполагается, что 2Т2≤ Т1.

В этом случае корни характеристического уравнения вещественные и уравнение (3.21) можно переписать в виде:

( T3p+1)(T4p+1) y(t) = x(t), (3.22)

где 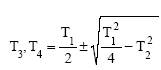- новые постоянные времени.

Передаточная функция звена

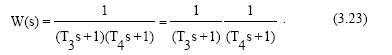
Из выражения (3.23) следует, что апериодическое звено второго порядка можно рассматривать как комбинацию двух апериодических звеньев первого порядка. Примерами апериодического звена второго порядка могут служить двойная RC цепочка, электродвигатель постоянного тока и др.

Колебательное звено.

Описывается дифференциальным уравнением

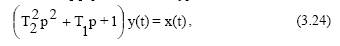
при Т1<2T2 корни характеристического уравнения комплексные и уравнение (3.24) переписывают в виде

(T2p2+2ξTp+1) y(t) = x(t), (3.25)

где Т - постоянная времени, определяющая угловую частоту свободных колебаний λ=1/Т; ξ - параметр затухания, лежащий в пределах 0<ξ<1.

Общепринятая запись передаточной функции колебательного звена имеет вид

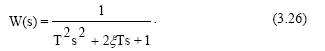
Амплитудно-фазовая частотная характеристика звена:

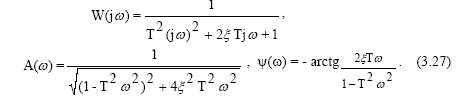
Временные характеристики представляют собой затухающие периодические процессы.

Примерами колебательного звена могут служить электрический колебательный контур, электродвигатель постоянного тока, маятник и др.

Консервативное звено.

Консервативное звено является частным случаем колебательного при ξ=0. Оно представляет собой идеализированный случай, когда можно пренебречь влиянием рассеяния энергии в звене.

Амплитудно-фазовая характеристика совпадает с вещественной осью. При 0<ω<1/T характеристика совпадает с положительной полуосью, а при ω>1/T – с отрицательной полуосью.

Временные характеристики соответствуют незатухающим колебаниям с угловой частотой 1/T.

Интегрирующие звенья

В звеньях интегрирующего типа линейной зависимостью 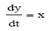связаны в установившемся режиме производная выходной величины и входная величина. В этом случае для установившегося режима будет справедливым равенство

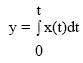, откуда и произошло название этого типа звеньев.

Идеальное интегрирующее звено.Уравнение и передаточная функция имеют вид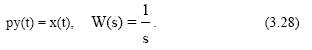

Амплитудно-фазовая частотная характеристика:

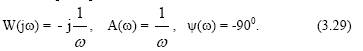
Переходная и импульсная функции:

Такое звено является идеализацией реальных интегрирующих звеньев.

Примерами идеальных интегрирующих звеньев могут служить операционный усилитель в режиме интегрирования, гидравлический двигатель, емкость и др.