Функция распределения двумерной случайной величины

ЛЕКЦИЯ 3

Корреляционный анализ. Многомерные случайные величины. Коэффициент корреляции. Функция регрессии. Двумерный нормальный закон распределения. Статистическая оценка коэффициента корреляции.

Глава 4.
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

Многомерные случайные величины

Функция распределения двумерной случайной величины

Многие экономические показатели определяются несколькими числами, являясь по сути многомерными. Например, уровень жизни населения подразумевает использование большого числа показателей: ВНП на душу населения, распределение доходов, наличие товаров и услуг, продолжительность жизни и т.д. Поэтому одна из основных задач экономического анализа – выявление наличия и силы взаимосвязи между различными экономическими показателями (фактически между случайными величинами). Например, между доходом и потреблением; между спросом на товар и его ценой; между уровнем инфляции и уровнем безработицы; между ВНП и уровнем жизни. Вследствие этого при проведении эконометрического анализа одно из главных мест занимает исследование взаимосвязей случайных величин, при которых реализация одной из случайных величин влияет на вероятность определенной реализации других случайных величин.

При рассмотрении вопросов, связанных с системами случайных величин, удобно пользоваться геометрической интерпретацией системы. Например, систему двух случайных величин {X₁, X₂} можно изобразить случайной точкой на плоскости с координатами X₁ и X₂. Часто вместо образа случайной точки для геометрической интерпретации пользуются образом случайного вектора

.

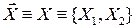В дальнейшем мы будем в зависимости от удобства пользоваться как одной, так и другой интерпретацией. Изложение мы проводить в основном для случая двумерных величин. Общий n-мерный случай рассматривается совершенно аналогично.

Функцией распределения F(x, y) двумерной случайной величины {X, Y} называется вероятность совместного выполнения двух неравенств: X<x, Y<y:

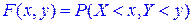. (4.1)

Свойства многомерной функции распределения, в целом, аналогичны свойствам функции распределения одномерной случайной величины.

Двумерная случайная величина {X,Y} называется дискретной, если каждая из случайных величин X и Y является дискретной. Ясно, что если дискретная величина X может принимать только значения x₁,…,x_n, а случайная величина Y – значения y₁,…,y_n, то двумерный случайный вектор {X,Y} может принимать только пары значений (x_i,y_j). Обычно системы двух ДСВ описывается матрицей распределения, т.е. прямоугольной таблицей, в которой записаны все вероятности p_ij того, что двумерная ДСВ примет значение (x_i,y_j).

Y X	y1	…	ym	PX
x1	p11	…	p1m	p1
…	…	…	…	…
xn	pn1	…	pnm	pn
PY	q1	…	qm

Сумма всех вероятностей p_ij , стоящих в матрице, равна единице как сумма вероятностей полной группы несовместных событий:

.

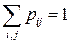Зная матрицу распределения системы двух ДСВ легко найти законы распределения отдельных случайных величин, входящих в систему:

.

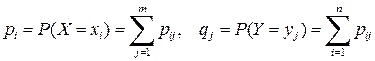Двумерная случайная величина {X,Y} называется непрерывной, если каждая из случайных величин X и Y является непрерывной. Система двух НСВ обычно описывается плотностью распределения:

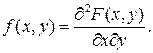(4.2)

Здесь и далее будем предполагать, что функция распределения F(x,y) всюду непрерывна и имеет всюду непрерывную частную смешанную производную второго порядка. Отметим два свойства плотности распределения f(x,y):

1) 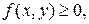2)

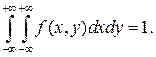
Зная плотность распределения f(x,y), можно найти функцию распределения:

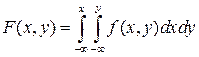. (4.3)