Алгоритм Форда – Беллмана

Рассмотрим теперь алгоритм, формирующий массив расстояний D для самого общего случая, т.е. для графа без контуров отрицательной длины.

Мы должны вычислить матрицу расстояний D[v]. За начальные (приближенные) значения D[v] возьмем веса дуг A[s,v]. Они будут соответствовать путям из s в v длиной в одну дугу. Если дуги (s→v) не существует, то начальное D[v] принимается равным +¥. Расстояние от источника до самого себя всегда считается равным 0.

Каким образом можно уточнить значения D[v]? Взять все пути из s в v длиной в две дуги и сравнить их с начальными D[v]. За окончательное значение D[v] принимается минимальное. Затем берутся пути длиной в три дуги и т.д. Процесс пересчета будет продолжаться до тех пор, пока не будут рассмотрены пути длиной в n-1 дугу. Нет смысла рассматривать пути длиной в n и более дуг, так как они будут содержать контур, который только увеличит суммарную длину пути.

Остается выяснить, каким образом из пути в k дуг можно получить все пути длиной в k+1 дугу. Из рис. 10.2 видно, что, добавив между s и v промежуточную (предпоследнюю) вершину u, мы автоматически удлиняем путь ровно на одну дугу. Длина старого пути равна D[v], длина нового пути равна D[u] + A[u,v].

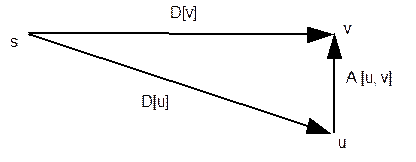
Рис. 10.2. Удлинение пути на одну дугу

АЛГОРИТМ Форда – Беллмана

Данные: Орграф G=<V,E> с n вершинами и выделенным источником s, заданный списками инцидентности PRED, матрица весов A[u,v], u,vÎV; граф не содержит контуров отрицательной длины.

Результаты: Расстояния D[v] от источника s до всех остальных vÎV.

1 begin

2 for vÎV do D[v]:= A[s,v];

3 D[s]:= 0;

4 for k:=1 to n-2 do

5 for vÎV-[s] do

6 for uÎPRED[v] do

7 D[v]:= min(D[v], D[u]+A[u,v]);

8 end.

Возможно, для вычисления D[v] нам не потребуются все n-2 итерации. Момент, когда D[v] будет вычислен окончательно, легко определить. Это произойдет, когда выполнение цикла 4 не вызовет изменения ни одного значения D[v].

Вычислительная сложность алгоритма О(nm). Если граф не является «разреженным» и число дуг m » n² , то можно считать вычислительную сложность равной О(n³).

Трассировка работы алгоритма Форда – Беллмана для графа с рис. 10.1:

k	D[1]	D[2]	D[3]	D[4]	D[5]
			+¥	+¥
					-1
					-1

Вопрос. Можно ли воспользоваться алгоритмом Форда – Беллмана для неориентированного графа, заменив каждое неориентированное ребро парой противоположно направленных дуг одного веса?

Ответ. Можно только в том случае, если при этом не образуется контур отрицательного веса, т.е. только для неориентированного графа с неотрицательными весами.

Алгоритм Дейкстры

Рассмотрим отдельно случай, когда веса всех дуг ориентированного графа неотрицательны.

Разделим все вершины V графа на два множества: T и V-T. T – рабочее множество, в нем содержатся вершины u Î T, для которых еще не известны окончательные D[u]. V-T – множество вершин, для которых уже известны настоящие расстояния.

В начальный момент в V-T содержится единственная вершина – источник s, все остальные вершины содержатся в T.

На каждой итерации основного цикла одна вершина из T будет переводиться в V-T. Этой вершиной r будет та, у которой D[r] минимально среди всех вершин множества T. Как только такая минимальная r будет найдена и переведена из T в V-T, для оставшихся вершин u Î T нужно будет пересчитать расстояния D[u].

Пересчет производится следующим образом: проведем путь от s к u через вершину r. Длина этого пути сложится из D[r] и веса дуги A[r,u]. Новое значение D[u] выберется как минимальное из старого D[u] и длины D[r]+A[r,u].

Алгоритм закончит работу, когда все вершины из множества T будут переведены в множество V-T. Доказательство корректности этого алгоритма будет приведено чуть позже, опишем сам алгоритм.

АЛГОРИТМ Дейкстры

Данные: Орграф G=<V,E> с выделенным источником s, матрица неотрицательных весов A[u,v], u,v Î V.

Результаты: Расстояния D[v] от источника s до всех остальных v Î V.

1 begin

2 for vÎV do D[v]:= A[s,v];

3 D[s]:= 0;

4 T:= V–[s];

5 while T<>0 do

6 begin

7 поиск вершины r из T, для которой
D[r]=min(D[u], uÎT);

8 T:= T–[r];

9 for uÎT do D[u]:= min(D[u], D[r]+A[r,u]);

10 end;

11 end.

Подсчитаем вычислительную сложность этого алгоритма.

Цикл 4 выполняется n-1 раз, так как именно столько вершин переводится из T в V-T. Внутри цикла при поиске минимальной просматривается не более n вершин; при пересчете расстояния пересчитываются не более, чем для n вершин. Окончательно получаем О(n²).

Докажем корректность первого шага алгоритма, когда из множества T, содержащего все вершины за вычетом источника, удаляется минимальная вершина r. Рассмотрим для иллюстрации модельный граф на рис. 8.27.

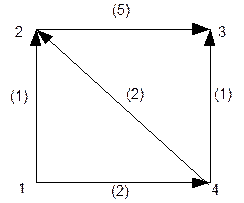
Рис. 10.3. Первый шаг алгоритма

В первый момент расстояния D[v] равны весам дуг A[s,v]. Минимальной вершиной r (вершина 2) является вершина с минимальным весом дуги (s→r) (дуга (1→2) с весом 1). Ни в одну другую вершину нельзя прийти более коротким путем, так как либо первая дуга (s→u) (дуга (1→4) с весом 2) (u ¹ r) будет уже длиннее, либо к дуге (s→r) нужно будет добавить хотя бы одну дугу, а веса всех дуг неотрицательны.

Полное математическое доказательство корректности читатель может найти в [1].

Трассировка работы алгоритма Дейкстры для модельного графа (рис. 10.4) представлена в табл. 1.

Рис. 10.4. Модельный граф

Таблица 1

Узел пересчета	D[1]	D[2]	D[3]	D[4]	D[5]	D[6]
–			+¥	+¥	+¥	+¥
					¥

Вопрос. Всегда ли можно воспользоваться алгоритмом Дейкстры для неориентированного графа с неотрицательными весами ребер?

Ответ. Да, всегда.