Принцип оптимальности беллмана

Решение задач математического программирования, которые могут быть представлены в виде многоэтапного многошагового процесса составляет предмет динамического программирования.

Динамическим программированием называется особый математический метод оптимизации решений, специально приспособленный к многошаговым процессам.

Процесс называется многошаговым, если он развивается во времени и распадается на ряд шагов или этапов.

Особенности динамического программирования:

1) Принятие решения по отношению к многошаговому процессу рассматривается не как единичный акт, а как целый комплекс взаимосвязанных решений.

Такая последовательность взаимосвязанных решений называется стратегией управления. Управлением же называется совокупность решений, принимаемых на каждом этапе с целью влияния на ход процесса.

Таким образом, решая задачи динамического программирования, мы рассматриваем управляемый экономический процесс, т.е. процесс, на ход которого можно влиять.

2) Оптимальное решение, которое принимается на данном шаге, не зависит от того, каким образом оптимизируемый процесс достиг настоящего состояния.

3) В методе динамического программирования поэтапное планирование многошагового процесса должно производиться так, чтобы при планировании каждого шага учитывалась не только выгода, получаемая на данном шаге, но и общая выгода, получаемая по окончании всего процесса.

Принцип оптимальности Беллмана. Каково бы ни было состояние системы перед очередным шагом, надо выбирать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным.

При решении оптимизационных задач методом динамического программирования необходимо учитывать на каждом шаге последствия, к которым приведёт в будущем решение, принимаемое в данный момент.

Исключением является последний шаг. Здесь процесс можно планировать так, чтобы последний шаг сам по себе приносил максимальный эффект.

Спланировав оптимально последний шаг, к нему можно пристроить предпоследний так, чтобы результат этих двух шагов был оптимальным и т.д.

Задачи динамического программирования решаются в два этапа.

I этап. Процесс условной оптимизации предполагает рассмотрение экономического процесса от конца к началу и решение на каждом шаге принимается при условиях, накладываемых предыдущим шагом.

Поэтому оптимальное решение, найденное при условии, что предыдущий шаг закончился определённым образом, называется условно-оптимальным.

II этап. Процесс безусловной оптимизации состоит в рассмотрении экономического процесса от начала к концу, в результате чего определяется оптимальное решение.

Математическая постановка задачи

динамического программирования

Рассматривается некоторый развивающийся во времени управляемый процесс. Предполагается, что этот процесс распадается на N шагов.

Состояние процесса на начало каждого шага характеризуется некоторым вектором S_i. Этот вектор называется вектором состояния процесса.

Множество всех состояний, в которых может находиться процесс за период из N шагов обозначается S. Известно начальное состояние процесса S₀. Развитие процесса заключается в последовательном переходе от одного состояния к другому (S_i →S_i+1).

Если процесс находится в состоянии S_i, то его состояние на следующем шаге S_i+1 определяется не только вектором S_i, но и решением u_i, принятым на i-м шаге (является некоторой функцией от величин S_i и u_i)

S_i+1 = φ(S_i, u_i).

Решение u_i на каждом шаге выбирается из множества U возможных решений: u₀, u₁, u₂,…, u_N-1; u_i ÎU.

Само развитие процесса можно описать последовательностью состояний: s₀, s₁, s₂,…, s_N; s_i ÎS.

Стратегией управления называют любую последовательность допустимых решений u₀, u₁, u₂,…, u_N-1, которая приводит процесс из начального состояния s₀ в конечное s_N.

Для полного описания процесса, каждой стратегии ставится в соответствие значение оценочной функции f_N(s) – эта функция называется целевой. Главное свойство этой функции – свойство аддитивности: f_N(s) – целевая оценочная функция равняется сумме оценочных функций r_i, которые получены на каждом шаге процесса при переходе из состояния s_i в состояние s_i+1

.

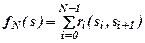Поскольку задано допустимое множество состояний s_i–х, допустимое множество решений u_i–х, правило перехода от одного состояния к другому и целевая функция, сформулируем общую задачу динамического программирования:

Найти стратегию управления u^*={ u₀, u₁, u₂,…, u_N-1},

позволяющую достигнуть экстремума функции

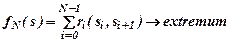
при условиях:

1) вектор начального состояния процесса S₀ задан

2) состояние на очередном i-м шаге определяется функцией

S_i+1 = φ(S_i, u_i).

s_i ÎS (i = 0,1,…, N) u_i ÎU (i = 0,1,…, N-1).

Математическая запись принципа оптимальности Беллмана. Пусть s₀ и s_N – начальное и конечное состояния N-шагового процесса.

Обозначим через f_N(s₀) – экстремальное значение целевой функции, полученное за N шагов при оптимальной стратегии u^* управления процессом, который начинался в состоянии s₀.

Допустим, на первом шаге было принято решение u₀, под воздействием которого процесс перешёл из состояния s₀ в состояние s₁ (s₀ →s₁). Полученный при этом эффект характеризуется величиной r₀(s₀, u₀).

Предположим, что после первого шага для управления процессом применялась оптимальная стратегия, которая обеспечивала на оставшихся N-1 шагах экстремальное значение f_N-1(s₁).

Значит, оптимальное значение эффекта на всех N шагах будет выражаться:

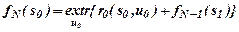
Обозначим через f_N-i(s_i) – экстремум целевой функции, полученной на последних N-i шагах, если сначала процесс находился в состоянии s_i, тогда

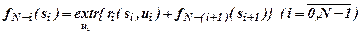
Полученное выражение есть математическая запись принципа оптимальности Беллмана. Это уравнение называется основным функциональным уравнением динамического программирования.