Алгоритм Форда-Фалкерсона

Доказательство теоремы 1 даёт алгоритм для построения минимального разреза (V_s, V_t), который отделяет v_s от v_t, и максимальный поток φ от v_s до v_t. Этот алгоритм был предложен Л. Фордом и Д. Фалкерсоном. Алгоритм начинает работу с известного допустимого потока φ (например, с нулевого). Потом расчеты развиваются в виде последовательности “расстановки пометок” (операция А), каждая из которых приводит к потоку с большей величиной (операция Б), или же завершается выводом, что рассмотренный поток максимален.

Будем предполагать, что пропускные способности c_j дуг сети целые числа.

Операция А (расстановка пометок). Каждая вершина может находиться в одном из трёх состояний: вершине приписана пометка и вершина просмотрена (то есть она имеет пометку и все смежные с ней вершины “обработаны”), вершина помечена, но не просмотрена, вершина не помечена. Пометка вершины v_i имеет один из двух видов: (+v_j, l) или (-v_j, l). Часть +v_j пометки первого типа показывает, что поток допускает увеличение вдоль дуги (v_j, v_i) на величину l. Часть -v_jпометки второго типа показывает, что поток допускает уменьшения вдоль дуги (v_i, v_j) на величину l. Сначала все вершины не имеют пометок.

Шаг 1. Источнику v_s присваивается пометка (+, v_s помечена, но не “просмотрена”.

Шаг 2. Возьмём произвольную помеченную, но не просмотренную вершину. Пусть оно имеет пометку ( 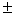v_r, l(v_j)). “Просмотрим” её, то есть просмотрим все вершины, смежные с ней, и пометем те из них, которые не помечены.

Всем непомеченным вершинам v_j, в которые входят дуги e_r из v_i и для которых φ(е_r) < c_r, приписываем пометку (+v_i, l(v_j)), где l(v_j) = min(l(v_i)), c_r - φ(е_r)).

Всем непомеченным вершинам v_j, из которых выходят дуги e_r в x_i и для которых φ(e_r) > 0, приписываем пометку (-v_i, l(v_j)), где l(v_j) = min(l(v_i)), φ(е_r)).

Теперь вершина v_i и помечена, и просмотрена, а вершина v_j, помечена, но не просмотрена.

Шаг 3. Повторять шаг 2 до тех пор, пока или сток – вершина v_t – будет помечена, или вершина v_t будет не помечена и никаких других пометок нельзя будет расставить. В первом случае переходим к операции Б, а во втором случае алгоритм заканчивает работу с максимальным потоком φ. Во втором случае множество помеченных и множество непомеченных вершин образовывают две стороны минимального сечения (V_s, V_t).

Операция Б (увеличения потока)

Шаг 4. Принять v = v_t и перейти к шагу 5.

Шаг 5. Если пометка в вершине v имеет вид (+z, l(v)), то изменить поток вдоль дуги (z, v) с φ(z, v) на φ(z, v) + l(v).

Если пометка в вершине v имеет вид (-z, l(v)), то изменить поток вдоль дуги (v, z) с φ(v, z) на φ(v, z) - l(v).

Шаг 6. Если z = v_s, то стереть все пометки и вернуться к шагу 1, чтобы снова начать расставлять пометки, но, используя уже улучшенный поток, который найден на шаге 5.

Если z ≠ v_s, то взять v = z и вернуться к шагу 5.

Рассмотрим на примере работу алгоритма Форда-Фалкерсона.

1. Возьмём поток, изображённый на рисунке 2.1 как начальный допустимый поток. Он имеет величину 3.

2. Присвоим источнику, вершине v₁, пометку (+, v₁ помечена, но не просмотрена.

3. Просмотрим вершины, смежные с вершиной v₁. Вершине v₂ присвоим пометку (+v₁, 1), а вершине v₃ – пометку (-v₁, 2) (φ(v₁, v₂) = 5 < 6 = c₁, φ(v₃, v₁) = 2 > 0). Вершина v₁ помечена и просмотрена, а вершины v₂ и v₃ помечены, но не пересмотрены.

4. Пересмотрим вершины, смежные с вершиной v₃. Из вершин, смежных с вершиной v₃, не помечены вершины v₄ и v₅. Вершине v₄ присвоим пометку (-v₃, 2), поскольку φ(v₄, v₃) = 4 > 0 и min(2, 4) = 2. Вершину v₅ не помечаем, поскольку φ(v₅, v₃) = 0.

5. Просмотрим вершины, смежные с вершиной v₂. Вершине v₅ присвоим пометку (+v₂, 1), поскольку φ(v₂, v₅) = 7 < 8 = c₅. Сток помечен. Переходим к операции В – увеличения потока.

6. Сток имеет пометку (+v₂, 1). Поэтому увеличиваем поток вдоль дуги (v₂, v₅) на 1.

7. Вершина v₂ имеет пометку (+v₁, 1). Поэтому увеличиваем поток вдоль дуги (v₁, v₂) на 1. Мы получили новый поток величины 4 (рис. 2.2).

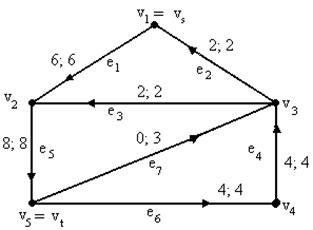
Рис. 2.2. Поток величины 4

8. Стираем все пометки.

9. Присваиваем вершине v₁ пометку (+,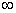

10. Пересматриваем вершины, смежные с вершиной v₁. Вершине v₃ присваиваем пометку (-v₁, 2). Вершину v₂ не помечаем, так как φ(v₁, v₂) = 6 = c(y₁).

11. Пересмотрим вершины, смежные с вершиной v₃. Вершине v₄ присвоим пометку (-v₃, 2), поскольку φ(v₄, v₃) = 4 > 0, l(v₃) = 2 и min(2, 4) = 2.

12. Пересмотрим вершины, смежные с вершиной v₄. Вершине v₅ присвоим пометку (-v₄, 2), так как φ(v₅, v₄) = 4 > 0,l(v₄) = 2 и min(2, 4) = 2. Сток помечен. Переходим к операции Б – увеличения потока.

13. Сток имеет пометку (-v₄, 2). Поэтому уменьшаем поток вдоль дуги (v₅, v₄) на 2.

14. Вершина v₄ имеет пометку (-v₃, 2). Поэтому уменьшаем поток вдоль дуги (v₄, v₃) на 2.

15. Вершина v₃ имеет пометку (-v₁, 2). Поэтому уменьшаем поток вдоль дуги (v₃, v₁) на 2. Мы получили новый поток величины 6 (рис. 2.3). По теореме 1 этот максимальный. Проверим это.

Рис. 2.3. Максимальный поток

16. Стираем все пометки.

17. Присваиваем вершине v₁ пометку (+, ).

18. Вершины, смежные вершине v₁, нельзя помечать, поскольку дуга (v₄, v₃) насыщенна – φ(v₁, v₂) = φ(е₁) = с(е₁) = 6, а через дугу (v₃, v₁) поток не передаётся. Сток остался не помеченным. Значит, полученный поток максимальный. Дуги (v₁, v₂) и (v₃, v₁) образуют минимальный разрез. Множество помеченных вершин образует ту его сторону, которая содержит источник: V_s = {v₁}. Непомеченные вершины образуют другую сторону разреза, который содержит сток: V_t = {v₂, v₃, v₄, v₅}. Построенный поток имеет вид φ(е₁) = 6, φ(е₅) = 8, φ(е₆) = 2, φ(е₄) = 2, φ(е₃) = 2, φ(е₂) = φ(е₇) = 0.