Упругие волны в безграничных средах

Зацепин А. Ф.

© Введение в физику акустического контроля: конспект лекций. / А.Ф.Зацепин. - Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. - 88 с.

ISBN

Конспект лекций является учебным пособием по курсу "Акустический контроль" для студентов специальности 190200 – Приборы и методы контроля качества и диагностики, которые обучаются на кафедре «Физические методы и приборы контроля качества» физико-технического факультета УГТУ-УПИ. Основное внимание сконцентрировано на явлениях, понятиях и принципах, положенных в основу современных методов акустического контроля.

Публикуется в рамках плана Уральского НОЦ "Перспективные материалы" (Award No. REC - 005 of the U.S. Civilian Research & Development Foundation (CRDF)) – Российско-американская программа поддержки фундаментальных исследований.

Библиогр.: 10 назв. Табл. 4. Рис. 42.

УДК 534.2:658.562.6(042.4)

ББК 22.32+30.607я73

ISBN Ó ГОУ Уральский государственный

технический университет - УПИ, 2005

© А.Ф. Зацепин, 2005

СОДЕРЖАНИЕ

ВВЕДЕНИЕ.. 3

1. Упругие волны в безграничных средах.. 3

1.1. Волновое уравнение. 3

1.2. Колебания и волны.. 3

1.3. Волновой фронт. Плоские, сферические и цилиндрические волны.. 3

1.4. Акустические колебания в газах и жидкостях. 3

1.5. Упругие колебания в твердых средах. Скорость распространения волн в упругой среде 3

1.6. Фазовая и групповая скорость. Дисперсия скорости. 3

1.7. Энергетические характеристики упругих волн. Вектор Умова-Пойнтинга. 3

1.8. Шкала интенсивности и амплитуд. 3

1.9. Акустические свойства сред. 3

1.10. Контрольные вопросы.. 3

2. Упругие волны в ограниченных средах.. 3

2.1. Волны Рэлея. 3

2.2. Головные волны.. 3

2.3. Волны Лэмба в жидком слое. 3

2.4. Волны Лэмба в твердых телах. 3

2.5. Волны в стержнях (волны Порхгаммера) 3

2.6. Контрольные вопросы.. 3

3. Прохождение волн через границУ сред.. 3

3.1. Коэффициенты отражения и прохождения. 3

3.2. Случай наклонного падения. Обобщенный закон Снеллиуса. 3

3.3. Прохождение акустической волны через границу жидкость – жидкость. 3

3.4. Энергетические соотношения на границе жидкость – жидкость и твердое
тело – твердое тело. 3

3.5. Критические углы.. 3

3.6. Явление незеркального отражения. 3

3.7. Угловая зависимость коэффициентов прозрачности. 3

3.8. Отражение волны от свободной поверхности твердого тела. 3

3.9. Отражение от двугранного угла. 3

3.10. Прохождение волн через тонкий слой на границе двух сред. 3

3.11. Влияние толщины слоя на прохождение акустических волн. 3

3.12. Контрольные вопросы.. 3

4. МЕТОДы акустического контроля.. 3

4.1. Теневой метод (метод прохождения) 3

4.2. Методы отражения. 3

4.3. Импедансный метод. 3

4.4. Метод свободных колебаний. 3

4.5. Резонансный метод. 3

4.6. Комбинированные методы.. 3

4.7. Пассивные методы.. 3

4.8. Способы осуществления акустического контакта. 3

4.9. Контрольные вопросы.. 3

ЛИТЕРАТУРА.. 3

Список сокращений и обозначений

АК – акустический контроль

АЧХ – амплитудно-частотная характеристика

НК– неразрушающий контроль

ОК – объект контроля

ПЭП – пьезоэлектрический преобразователь

УЗ – ультразвук

УЗК – ультразвуковые колебания

ЭМА – электромагнитно-акустический

ВВЕДЕНИЕ

В связи с высокими требованиям к качеству выпускаемой продукции большое значение в современном промышленном производстве имеют физические методы контроля. Их применение позволяет избежать излишних временных и материальных затрат при одновременном повышении надежности и качественных показателей изделий. В принципе, любое несоответствие продукции установленным техническим требованиям является дефектом. Под дефектоскопией понимают комплекс косвенных методов неразрушающего контроля материалов, деталей машин и механизмов, а также разработку соответствующей аппаратуры, методик испытаний и норм браковки. Диагностика – наука о распознавании состояния технических систем. Она включает в себя выявление и изучение признаков, характеризующих состояние диагностируемой системы в целом, что позволяет на этой основе дать прогноз ее ресурса.

В настоящее время в различных отраслях промышленности широкое распространение получили акустические методы неразрушающего контроля. По сравнению с другими методами контроля они обладают важными преимуществами: имеют высокую чувствительность к опасным внутренним дефектам типа трещин, инородных включений и других нарушений сплошности контролируемого материала. Ультразвуковые методы контроля и диагностики характеризуются большой производительностью, обеспечивают возможность проведения процедуры контроля непосредственно на рабочих местах без прерывания технологического процесса.

Успешное применение ультразвуковых методов НК на практике, также как и их дальнейшее совершенствование, невозможны без понимания физической природы явлений, положенных в основу работы соответствующих приборов и методик контроля качества. Акустика это раздел физики, который изучает процессы упругих колебаний и законы их распространения в различных средах. Упругие механические колебания, распространяющиеся в воздухе, обычно воспринимаются как звуки. Человеческое ухо различает акустические колебания в диапазоне от 16 Гц до 20 кГц. Если же их частота превышает 20 кГц, то такие колебания называют ультразвуковыми. В отличие от других видов колебаний особенностью акустических колебаний является необходимость наличия материальной среды для их возникновения и распространения. Акустические колебания ультразвуковой частоты могут быть возбуждены в твердых, жидких и газообразных средах. При этом колебательное движение возбужденных частиц среды благодаря наличию упругих сил между ними вызывает распространение упругой ультразвуковой волны, сопровождаемое переносом энергии. Знание особенностей генерации акустических колебаний и распространения волн в различных средах, законов их взаимодействия с границами раздела позволяют с наибольшей эффективностью применять указанные явления на практике.

В основу предлагаемого учебного пособия положены материалы курса лекций «Акустический контроль», читаемого студентам кафедры «Физические методы и приборы контроля качества» на физико-техническом факультете УГТУ-УПИ. Пособие построено таким образом, чтобы дать возможность студентам наиболее последовательно и логично усвоить изучаемый материал. В первых трех главах пособия рассматриваются основы физики колебаний малой амплитуды, закономерности распространения, отражения преломления и трансформации акустических волн. Даны определения основных понятий, применяемых в геометрической и волновой акустике. Основное внимание уделено обсуждению физики процессов с использованием соответствующего математического аппарата. В последней главе описана классификационная система активных и пассивных методов акустического контроля и диагностики, дана их краткая характеристика. Каждая глава завершается контрольными вопросами, предназначенными для закрепления и улучшения усвоения изучаемого материала.

Упругие волны в безграничных средах

В данной главе вводится ряд определений и понятий физической акустики, рассматриваются волны в безграничных средах, дается представление о волновом уравнении и его характеристических свойствах.

Волновое уравнение

Многообразие различных волновых процессов в первом приближении описывается волновым уравнением

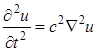, (1.1)

где ;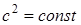

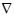– гамильтониан – инвариантный оператор.

Это линейное гиперболическое уравнение второго порядка. В случае упругих сред, о чем будет сказано ниже, оно описывает малые свободные колебания. Под функцией 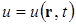понимаются различные физические величины: давление, смещение, скорость смещения частиц среды и т. д.

В случае одного пространственного измерения уравнение (1.1) для плоского случая приобретает наиболее простой вид:

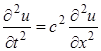. (1.2)

Величина с постоянна и имеет размерность скорости. Далее будет ясно, что 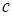соответствует скорости распространения возмущения. Решением уравнения (1.2) является суперпозиция двух функций:

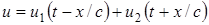. (1.3)

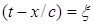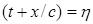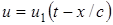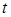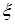Отметим далее важное свойство уравнения (1.2), справедливое и для уравнения (1.1). Величины , называются характеристиками уравнения (1.2). Будем полагать, что . Находя полную производную по от , получим, что 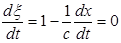, откуда 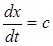. Так как 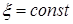, то возмущение, имеющее в некоторый момент времени 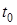заданную форму 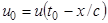, не изменит ее и в любой другой момент времени. Таким образом, возмущения распространяются, не изменяясь по характеристикам, с постоянной скоростью. Это важное характеристическое свойство уравнения (1.2). В случае трех пространственных переменных говорят уже о характеристических поверхностях.

В следующем параграфе мы еще вернемся к волновому уравнению (1.2) и его решению (1.3). Здесь же отметим одно обстоятельство, касающееся терминологии. Функцию вида 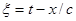в определенном контексте называют фазой. Применительно к уравнению (1.2) и решению (1.3) фаза совпадает с характеристикой. В общем случае, это может быть не так, поэтому в следующем параграфе и особенно в параграфе, посвященном явлению дисперсии, понятие фазы не следует отождествлять с характеристиками уравнения (1.2).

Колебания и волны

Колебания – процессы, при которых состояние системы воспроизводится через определенный промежуток времени. В акустике рассматриваются упругие колебания. Акустические колебания – механические колебания частиц упругой среды. Под упругой средой понимается среда, в которой напряжение есть линейная функция деформации. Колебания можно разделить на две большие группы: свободные и вынужденные. Свободные колебания система совершает, будучи предоставлена самой себе. Реально из-за наличия трения, диссипативных процессов и пр. свободные колебания являются затухающими. Вынужденные колебания система совершает под действием возмущающей силы. Если собственные частоты колебательной системы совпадают с частотой вынуждающих воздействий, то система входит в резонанс.

Упругие колебания в жидкостях и газах характеризуются одной из следующих величин: изменением давления p или плотности r, смещением частиц из положения равновесия u, скоростью колебательного движения v, потенциалом смещения χ или колебательной скорости φ. Следует отличать изменение давления или плотности, связанное с распространением акустических волн, от их статистического (среднего) значения. Все перечисленные величины взаимосвязаны, например: u = grad c; v = grad j; v 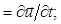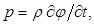где ρ – плотность среды; t – время.

Колебания, возникнув в одной точке среды, за счет упругого взаимодействия частиц распространяются с некоторой скоростью c. Волной называют процесс распространения упругого возмущения среды. С математической точки зрения волной имеет смысл называть решение волновых уравнений – главным образом линейных и квазилинейных гиперболических (они имеют одну характерную особенность).

При всем многообразии волновых явлений, линейные волны в одномерном случае могут быть представлены функциями вида

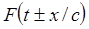. (1.4)

Величина 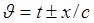имеет смысл фазы. Отметим здесь, что фаза определена с точностью до аддитивной постоянной. В этой связи уместно сказать, что функция

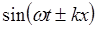(1.5)

также является решением волнового уравнения (1.2) при определенных соотношениях между 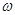и 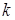. Для синусоидальных функций фазой будет функция

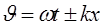. (1.6)

Здесь, как и в формулах (1.4), (1.5) знаки «минус» и «плюс» обозначают направление распространения волны: вдоль оси x и в обратном направлении, соответственно.