Модели фильтрационного течения

Теория фильтрации строится на представлении породы и заполняющего ее флюида сплошной средой. Это означает необходимость осреднения кинематических и динамических параметров по пространству, которое требует малости элементов системы флюид – порода, но при этом они должны быть достаточно большими по сравнению с размерами пустот и зерен породы. При этом предполагается, что в одном и том же элементарном объеме содержатся одновременно порода и флюид.

При исследовании фильтрационного течения в подземной гидромеханике изменением температуры флюида пренебрегается по причине малых скоростей течения и значительного теплообмена со скелетом пород, вследствие значительной поверхности контакта и значительного превышения теплоёмкости горных пород над теплоёмкостью флюида. Таким образом, процесс течения предполагается изотермическим. Необходимо отметить, что в отдельных случаях (тщательное изучение призабойной зоны, использование термических методов интенсификации добычи флюидов) используют и общую постановку – с учётом изменения температуры не только флюида, но и породы.

Для процессов, происходящих в нефтегазовых пластах при разработке, характерно наличие периодов изменения параметров течения во времени (пуск и остановка скважин, проведение работ по интенсификации притока). Такие процессы называют неустановившимися (нестационарными), а сами модели течения нестационарными. Те же модели, которые описывают процессы, не зависящими от времени, называют стационарными (установившимися). При этом в данных моделях, по причине малости изменения скорости и значительного преобладания сил сопротивления над инерционными силами, уравнение количества движения используется, не зависящим от времени, и пренебрегается изменением импульса по пространству.

Моделирование фильтрационного течения по отношению к пространственному изменению параметров может проводиться в одномерной, плоской и пространственной постановках. Одномерная постановка рассматривается в том случае, когда параметры являются функцией только одной переменной – это течение по прямой или кривой.

Модели флюидов

По степени сжимаемости. Природный газ способен значительно изменять свой объём при изменении давления, вода и нефть в довольно значительном диапазоне давлений (приблизительно до 20МПа) практически несжимаемы, а при высоких давлениях обладают упругими свойствами. В связи с указанными факторами различают модели сжимаемой, несжимаемой и упругой среды. Построение каждой из указанной модели требует привлечения эмпирических уравнений состояния – соотношений, связывающих изменение объёма с изменением давления.

Гомогенные и многофазные модели. В области контакта флюидов при вытеснении одного другим или при выделении одного флюида из другого в каждом микрообъёме содержится два или больше флюидов, занимающих отдельные четко различимые объёмы (пузырьки газа в жидкости, капли или плёнки в газе) и взаимодействующих на поверхностях раздела. Такие системы называют многофазными (двух, трёх и т.д.), в отличие от многокомпонентных смесей (природный газ, нефть), в которых взаимодействие происходит на молекулярном уровне, и поверхности раздела выделить нельзя. В гидродинамике такие среды называют однофазными или гомогенными.

Ньютоновские и неньютоновские жидкости. В процессе движения флюиды испытывают различные деформации (сжатие, кручение, растяжение и т.д.) при изменении нагрузки (трение соседних объёмов, внешние силы), которая, отнесённая к единице площади, получила название напряжения. Само соотношение, связывающее деформацию или скорость изменения деформации с напряжением, называется реологическим соотношением или законом. Наиболее часто, применительно к жидкостям, для описания действия касательных напряжений t_xy на сдвиговую деформацию применяют соотношение Ньютона 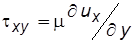, где u_x– скорость в направлении х; у– направление, перпендикулярное х.

Довольно часто движение флюидов не подчиняется данному закону, например, при страгивании пластовой нефти требуется некоторое, отличное от нулевого, напряжение, чтобы разорвать образованные пластовой водой коллоидные структуры. Такие среды называются неньютоновскими, а модель – моделью неньютоновского течения.

Модели коллекторов

Моделирование коллекторов и, соответственно, классификация их параметров проводится по трём направлениям: геометрическое, механическое и связанное с наличием жидкости.

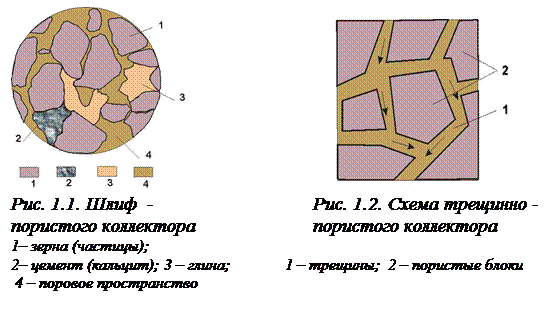
Геометрические модели.С геометрической точки зрения, все коллектора можно подразделить на две большие группы: гранулярные (поровые) (рис. 1.1) и трещинные (рис.1.2). Ёмкость и фильтрация в пористом коллекторе определяется структурой порового пространства между зёрнами породы. Для второй группы характерно наличие развитой системы трещин, густота которых зависит от состава пород, степени уплотнения, мощности, структурных условий и так далее.

Чаще всего имеют место коллектора смешанного типа, для которых ёмкостью служат трещины, каверны, поровые пространства, а ведущая роль в фильтрации флюидов принадлежит развитой системе микротрещин, сообщающих эти пустоты между собой. В зависимости от вида путей фильтрации или главных вместилищ флюида различают коллектора: трещинно-пористые, трещинно-каверновые и т.д. При этом первая часть в названии определяет вид пустот, по которым происходит фильтрация.

С целью количественного описания фильтрационно - ёмкостных параметров реальные сложные породы заменяют идеализированными моделями.

Рис. 1.3. Слепок поровых каналов сцементированного песчаника

Идеализированные модели пористых сред.Реальные горные породы имеют очень сложную геометрию (рис.1.3) порового пространства или трещин. Кроме того, размеры частиц гранулярных коллекторов или трещин в трещиноватых породах меняются в очень широких пределах – от микрометров до сантиметров. Естественно, что математическое описание течения через столь хаотическую структуру невозможно и, следовательно, необходима некоторая идеализация структуры.

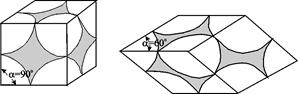Рис. 1.4. Элемент фиктивного грунта

Фиктивный грунт – среда, состоящая из шариков одного размера, уложенных во всем объёме пористой среды одинаковым образом по элементам из восьми шаров в углах ромбоэдра (рис.1.4). Острый угол раствора ромбоэдра a меняется от 60 до 90^о. Наиболее плотная укладка частиц при a=60^о и наименее плотная при a=90^о (куб)

С целью более точного описания реальных пористых сред в настоящее время предложены более сложные модели фиктивного грунта: с различными диаметрами шаров, элементами не шарообразной формы и так далее.

Идеальный грунт – среда, состоящая из трубочек одного размера, уложенных одинаковым образом по элементам из четырех трубочек в углах ромба. Плотность укладки меняется от угла раствора ромба.

Идеализированные модели трещинно-пористых сред. Трещинно-пористые коллекторы рассматриваются как совокупность двух разномасштабных пористых сред (рис.1.2): системы трещин (среда 1), где пористые блоки играют роль “зёрен”, а трещины – роль извилистых “пор” и системы пористых блоков (среда 2).

В простейшем случае трещинный пласт моделируется одной сеткой горизонтальных трещин некоторой протяженности (рис.1.5), причём все трещины одинаково раскрыты и равно отстоят друг от друга (одномерный случай).

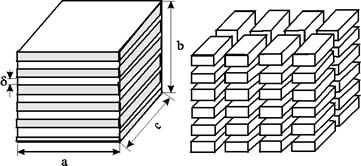Рис.1.5. Схема одномерной Рис.1.6 Схема пространственной модели трещинной среды модели трещинной среды

В большинстве случаев трещинный пласт характеризуется наличием двух взаимно-перпендикулярных систем вертикальных трещин (плоский случай). Такая порода может быть представлена в виде модели коллектора, расчленённого двумя взаимно-перпендикулярными системами трещин с равными величинами раскрытия dи линейного размера блока породы l. В пространственном случае используют систему трёх взаимно-перпендикулярных систем трещин (рис.1.6).

Механические модели. Реологические модели горных пород. Всякое изменение сил, действующих на горные породы, вызывает их деформацию, а также изменение внутренних усилий – напряжений. Таким образом, динамическое состояние горных пород, как и флюидов, описывается реологическими соотношениями. Обычно реологические зависимости получают в результате анализа экспериментальных данных, натурных исследований или физического моделирования. Если объём пустот не изменяется или изменяется так, что его изменением можно пренебречь, то такую среду можно назвать недеформируемой. Если происходит линейное изменение объёма от напряжения, то такая среда – упругая, иначе ещё её называют кулоновской. К таким средам относятся песчаники, известняки, базальты. В упругих телах при снятии нагрузки объём восстанавливается полностью и линия нагрузки совпадает с линией разгрузки. Многие породы деформируются с остаточным изменением объёма, т.е. линия нагрузки не совпадает с линией разгрузки. Такие породы называются пластичными (глины), текучими (несцементируемые пески) или разрушаемыми.

Модели по ориентированности в пространстве. Горные породы необходимо разделять по ориентированности изменения их характеристик в пространстве. С этой позиции выделяют изотропные и анизотропные тела. Изотропия – это независимость изменения физических параметров от направления, анизотропия – различные изменения по отдельным направлениям. Понятие ориентированности, применительно к коллекторам, связано с геометрией расположения частиц, трещин. Частицы горной породы могут располагаться хаотически и упорядочно (иметь геометрическую ориентацию). Упорядочные структуры – анизотропны по поверхностным параметрам.