Элементы теории случайных процессов
МАТЕРИАЛЫ
ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОТДЕЛЕНИЯ
СПбГЭТУ (ЛЭТИ)
Курс «Теория вероятностей и математическая статистика»
Кафедра ВМ-2
Курс 3
Семестр 5
Санкт-Петербург
2009 г.
ПРОГРАММА КУРСА.
ЭЛЕМЕНТАРНЫЕ СВОЙСТВА ВЕРОЯТНОСТИ
Элементы комбинаторики. Классическое и геометрическое определения вероятности. Действия над событиями. Основные свойства вероятности. Условная вероятность, независимость событий. Формулы полной вероятности и Байеса. Схема Бернулли, предельные теоремы для схемы Бернулли: теорема Пуассона и теоремы Муавра-Лапласа.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Аксиомы теории вероятностей. Случайные величины. Дискретные и абсолютно непрерывные случайные величины. Примеры: случайные величины, имеющие биномиальное, пуассоновское, равномерное, показательное, нормальное распределения. Числовые характеристики случайных величин. Вычисление их для классических распределений: распределения Бернулли, биномиального, пуассоновского, равномерного для конечной совокупности, равномерного, показательного, нормального. Случайные векторы и их распределения. Независимость случайных величин. Нормальный случайный вектор. Вектор, имеющий равномерное распределение в ограниченной области. Вычисление распределений одномерных компонент случайных векторов. Неравенство Чебышева. Закон больших чисел. Центральная предельная теорема. Коэффициент корреляции. Условные распределения и условные математические ожидания.
Математическая статистика
Общая статистическая модель. Выборка. Выборочные характеристики: выборочное математическое ожидание, выборочная дисперсия, выборочные моменты, выборочная медиана. Выборочный подход к построению оценок. Примеры. Другие методы нахождения оценок: метод моментов, метод максимального правдоподобия, оценки метода наименьших квадратов. Основные требования к оценкам: состоятельность, несмещенность. Общие понятия эффективности оценок.
Доверительные интервалы. Примеры: Доверительный интервал для математического ожидания нормальной выборки при известной и неизвестной дисперсии. Доверительный интервал для дисперсии при известном и неизвестном математическом ожидании.
Проверка простых гипотез. Критерии Стьюдента. Примеры. Непараметрические критерии: критерий Колмогорова и критерий 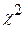 (хи-квадрат). Критерий
(хи-квадрат). Критерий 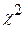 при наличии мешающих параметров.
при наличии мешающих параметров.
Техника использования различных статистических таблиц.
ЭЛЕМЕНТЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Общие понятия. Корреляционная функция. Случайные процессы с дискретным и непрерывным временем. Пуассоновский случайный процесс и его приложения. Понятие о марковских процессах с примерами из теории массового обслуживания.
ЛИТЕРАТУРА.
Основная литература.
- А.Н.Бородин. Элементарный курс теории вероятностей и математической статистики. СПб.: Издательство «Лань», 1998.- 224с.
- Е.С. Венцель, Л.А. овчаров Теория вероятностей. М: Наука, 1969.
- Ю.А.Розанов. Случайные процессы.Краткий курс. М: Наука, 1971, 286с.
- Г. Крамер Математические методы статистики. 2-изд. М.Мир, 1975.
- Сборник задач по математике для ВТУЗов. Ч.3 под ред. А.В. Ефимова: Учеб.пособие для ВТУЗов. –М.: Наука, 1984, 1990.
- В.А.Егоров, С.В.Малов, И.В.Соколова. Специальные главы теории вероятностей: методические указания. СПбГЭТУ«ЛЭТИ», 1997.
- В.А.Егоров, А.М.Коточигов, С.Н.Солнышкин. Методы решения задач по теории вероятностей (дискретные распределения): методические указания. СПбГЭТУ«ЛЭТИ», 2007.
Дополнительная литература.
- А.Н.Ширяев. Вероятность. М. «Наука» 1976.
- Э.Леман. Проверка статистических гипотез. М. Наука, 1964.
Вопросы к экзамену
1. Основные комбинаторные формулы.
2. Классическое и геометрическое определения вероятности.
3. Основные свойства вероятности.
3. Условная вероятность, независимость событий.
4. Формулы полной вероятности.
5. Формула Байеса.
6. Схема Бернулли.
7. Теорема Пуассона.
8. Локальная теорема Муавра-Лапласа.
9. Интегральная теорема Муавра-Лапласа.
10. Аксиомы теории вероятностей.
11. Случайные величины: определение и примеры.
12. Нормальная и равномерная случайные величины.
13. Числовые характеристики случайных величин.
14. Случайные векторы и их распределения.
15. Неравенство Чебышева, закон больших чисел.
16. Коэффициент корреляции.
17. Выборка. Выборочные характеристики.
18. Выборочный подход к построению оценок. Примеры.
19. Гистограмма как оценка для плотности распределения.
20. Оценки метода моментов.
12. Несмещенность и состоятельность оценок.
21. Понятие об эффективности оценок.
22. Оценки метода максимального правдоподобия.
23. Оценки метода наименьших квадратов.
34. Доверительные интервалы для математического ожидания.
35. Доверительные интервалы для дисперсии.
36. Основные методы проверки статистических гипотез (теория Неймана-Пирсона).
37. Проверка простых гипотез примеры.
38. Критерий Колмогорова. Критерий хи-квадрат.
39. Критерий Стьюдента.
40. Общие понятия о случайных процессах с дискретным и непрерывным временем.
41. Процесс Пуассона.
42. Понятие о Марковских процессах, основные характеристики, примеры.
