Теорема. Для того чтобы ряд сходился равномерно на множестве X, необходимо и достаточно, чтобы .

Для установления на практике равномерной сходимости рядов пользуются достаточными признаками.

v Признак равномерной сходимости, основанный на сравнении функционального ряда со сходящимся числовым.

Теорема. Если члены ряда удовлетворяют неравенствам , где , а числа, не зависящие от , и, если ряд сходится, то ряд сходится равномерно на множестве X.

v Достаточные условия непрерывности суммы ряда.

Теорема. Если функции определены и непрерывны на множестве X и ряд сходится равномерно к сумме S(x) , то эта сумма будет непрерывна на множестве X.

v Свойства равномерно сходящихся рядов.

Теорема. Если функции определены и непрерывны на отрезке и ряд сходится равномерно на к сумме , то его можно почленно интегрировать на этом отрезке

.

Теорема. Если функции определены на отрезке и существуют непрерывные производные на интервале , а ряд сходится на и равномерно сходится ряд , то сумма ряда имеет на интервале непрерывную производную, причем, .

Таким образом, ряд 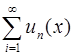можно почленно дифференцировать.

Степенной ряд

Степенным рядом называется ряд вида:

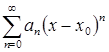, (9)

где 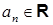‑ числовые коэффициенты, 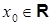‑ фиксированное число и 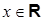‑ переменная.

Если зафиксировать 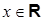, то получится числовой ряд. Если этот числовой ряд сходится, то говорят, что степенной ряд (9) сходится в точке 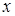. Множество всех точек 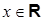, в которых ряд (9) сходится, называют множеством сходимости ряда (9).

Пример. Ряд 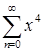сходится абсолютно при 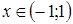, т.к. 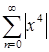при 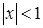сходится. Если же 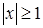, то 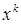не стремится к нулю, т.е. не выполнено необходимое условие сходимости и ряд расходится. Таким образом, множеством сходимости ряда 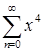является .

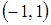Множество сходимости всякого ряда (9) есть промежуток, середина которого находится в точке 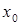. Промежуток сходимости может быть отрезком, полуинтервалом, интервалом, бесконечным промежутком или промежутком нулевой длины, т.е. точкой 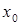. Число 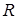, равное половине длины промежутка сходимости, называют радиусом сходимости. Радиус сходимости ряда (9) может быть вычислен следующим образом:

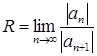, если такой предел существует;

1. 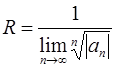, если такой предел существует.

Если в формулах 2. и 3. пределы равны 0, то 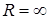. Если пределы равны 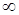, то .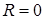

Если 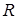‑ конечное число, то промежуток 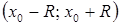принадлежит множеству сходимости. В ряде случаев множеству сходимости могут принадлежать также точк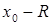и и .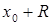

Пример. Ряд 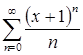имеет радиус сходимости .

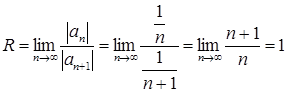Значит, интервал 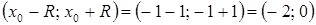входит в промежуток сходимости. Исследуем сходимость ряда на концах интервала 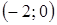. При 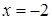получаем ряд 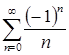, который сходится по признаку Лейбница. При 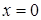получаем ряд 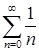, который расходится. Таким образом, промежуток сходимости ряда – полуинтервал .

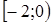Пример. Ряд 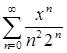имеет радиус сходимости 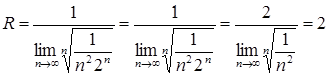. Значит, интервал сходимости .

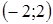Изучим сходимость ряда на концах этого интервала. При 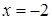получаем ряд 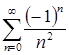, который сходится абсолютно. При 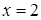получаем ряд 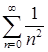, который также сходится. Значит, промежуток сходимости – отрезок .

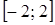Если функция 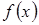в точке 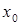имеет производные любого порядка, то для нее можно построить степенной ряд:

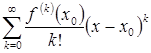(10)

Этот ряд называется рядом Тейлора для функции 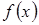в точке .

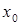Множество сходимости ряда (10) не всегда совпадает с областью определения функции 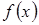, а его сумма не обязательно равна 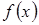. Если сумма ряда (10) совпадает с 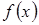на множестве 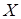, то можно написать:

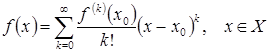(11)

В этом случае говорят, что 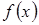на множестве 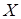разложена в степенной ряд(11). Справедливы следующие разложения:

, .

,

, .

, .

, .

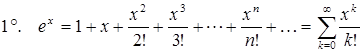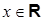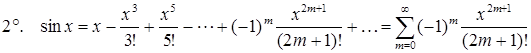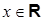
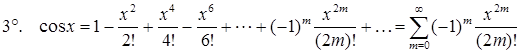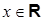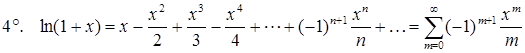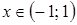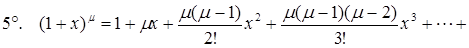
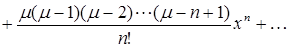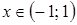При разложении функций в степенные ряды бывает удобным использовать разложения .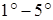

Пример. Разложить по степеням 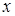функцию .

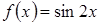Если обозначить 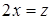, то, используя разложение 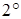, получаем: .

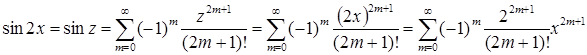Поскольку разложение 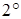справедливо для 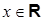, то 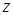может быть любым действительным числом.

Пример. Разложить по степеням 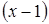функцию .

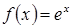Обозначив 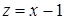и использовав разложение 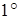, получим .

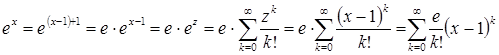Это разложение справедливо для 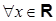, поскольку 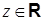может быть любым числом.

Ряды Фурье

Рассмотрим функциональные ряды, суммы которых, в отличие от степенных рядов, имеют непустое конечное множество точек разрыва в области задания.

Функция называется кусочно-непрерывной на отрезке 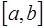, если она непрерывна всюду, кроме конечного числа точек разрыва первого рода. Другими словами, область ее определения можно разбить на конечное число частичных отрезков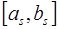 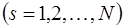, на каждом из которых:

1. функция 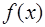ограничена и непрерывна во внутренних точках;

2. На концах каждого отрезка существуют конечные односторонние пределы , .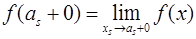

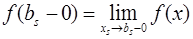
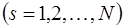Под интегралом функции 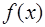понимается число .

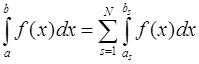Можно доказать, что для кусочно-непрерывной на отрезке 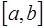функции 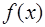существует обобщенная первообразная 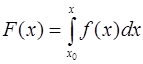( 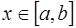, 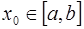), и, следовательно, .

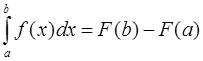Функция 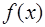называется кусочно-дифференцируемой (или кусочно-гладкой) на 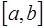, если производная 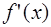кусочно-непрерывна на отрезке .

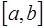Пусть функци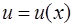и и 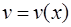кусочно-непрерывны на отрезке 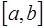. Скалярное произведение этих функций можно определить как .

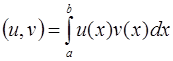Можно показать, что произведение двух кусочно-непрерывных на отрезке 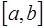функций есть функция кусочно-непрерывная на этом отрезке и, следовательно, ее определенный интеграл на этом отрезке существует.

Тогда , .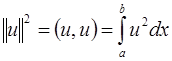

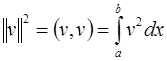Число 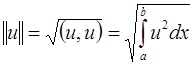называется нормой функции .

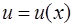Очевидны свойства скалярного произведения:

1. 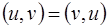– свойство коммутативности или симметрии;

2. 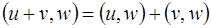– свойство ассоциативности или сочетательности;

3. 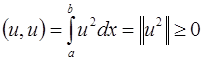, причем .

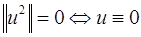Функци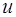и и 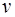называются ортогональными, если 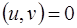, при этом , .

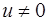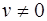Рассмотрим основную систему тригонометрических функций общего периода :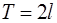

.

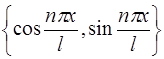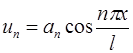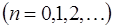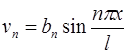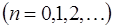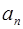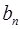Функции , и , называются основными гармониками. Их графиками являются синусоиды с амплитудами соответственно и . Гармоника 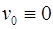и поэтому не рассматривается.

Лемма. Основные тригонометрические функции попарно ортогональны на любом промежутке, длина которого равна общему периоду 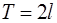этих функций, т.е. для стандартного отрезка 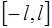справедливы условия ортогональности:

I. 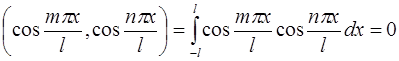при ;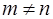

II. 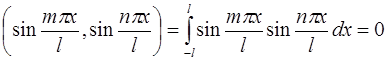при ;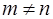

III. .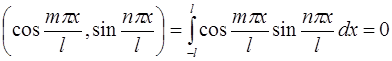

Условия ортогональности проверяются непосредственным интегрированием, в ходе которого используются формулы тригонометрии:

1) ;

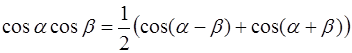2) ;

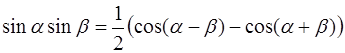3) .

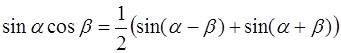Например, при :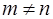

1)

,

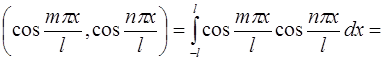
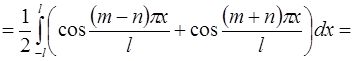
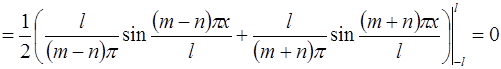т.к. 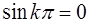при целых значениях ;

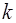2)

;

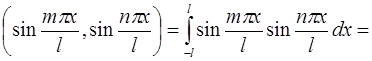
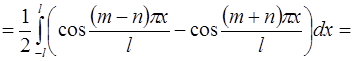
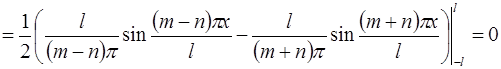3)

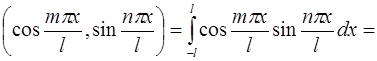
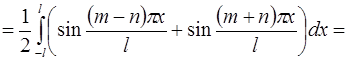
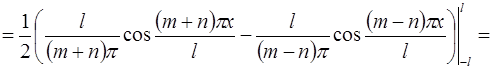
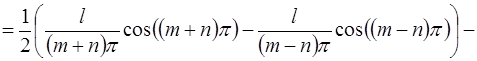
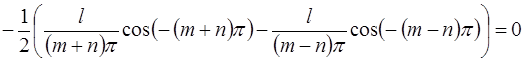
Пусть 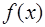– кусочно-непрерывная периодическая функция периода .

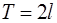Можно попытаться провести т.н. гармонический анализ 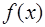, т.е. представить эту функцию в виде суммы конечного или бесконечного числа гармоник того же периода :

,

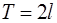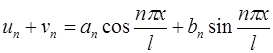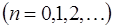
Таким образом, можно прийти к тригонометрическому ряду Фурье:

.

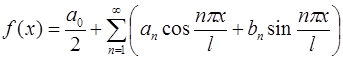Коэффициент нулевой гармоники обычно берется с множителем .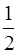

Исторически эта задача впервые возникла при математической обработке результатов наблюдения высоты приливной волны, которая периодически повторяется с течением времени. Гармонический анализ высоты приливной волны позволил дать долгосрочные предсказания ее величины, что было весьма важно для мореплавателей.

Предположим, что ряд:

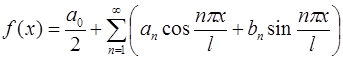
сходится на отрезке 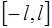и допускает почленное интегрирование, в результате которого получится следующее:

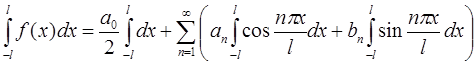
Так как из условий ортогональности:

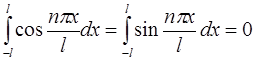
при 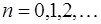, то получается

.

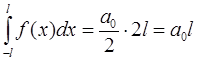Отсюда: .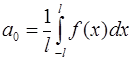

Интересно отметить, что свободный член тригонометрического ряда Фурье 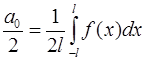представляет собой среднее значение периодической функции .

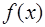Если умножить левую и правую части ряд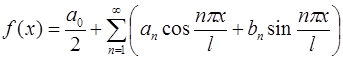а на 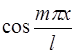и почленно проинтегрировать, то получится:

.

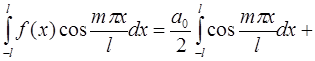
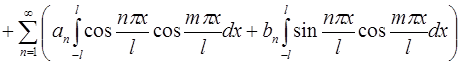Предварительно, следует отметить, что:

,

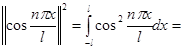
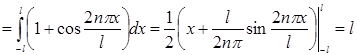т.е. .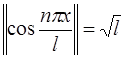

Отсюда, в силу условий ортогональности, а также с учетом нормировки, получается:

.

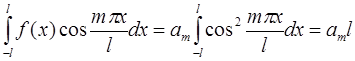Следовательно: 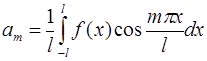, а значит, заменяя 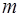на 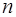(что по смыслу формул допустимо), можно получить:

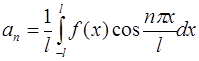
Аналогично, умножая обе части ряда на 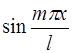и почленно интегрируя, получим:

.

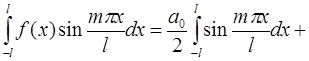
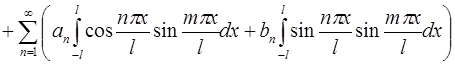В данном случае условие нормировки:

,

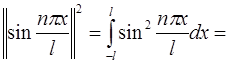
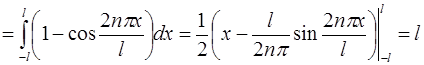т.е. .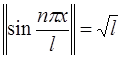

В силу условий ортогональности:

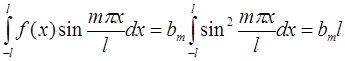
Следовательно, 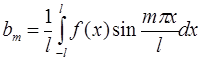, а значит:

.

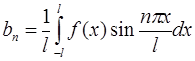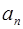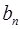
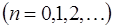Числа и называются коэффициентами Фурье функции .

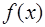Тригонометрический ряд:

,

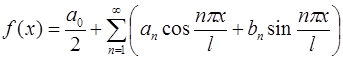коэффициентами которого являются коэффициенты Фурье данной периодической функции 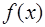называется ее тригонометрическим рядом Фурье, независимо от того, будет ли сумма этого ряда равна функции 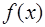или нет. В последнем случае говорят, что функция 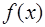порождает ряд Фурье:

,

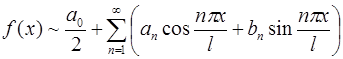где знак ~ означает «соответствует».

Теорема сходимости. Пусть периодическая функция , определенная на , кроме, может быть, точек ее разрывов, и имеющая период , является кусочно–дифференцируемой (или кусочно–гладкой) на любом промежутке, длина которого равна периоду этой функции.

Тогда:

1. Ее тригонометрический ряд Фурье сходится для любого значения 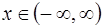, т.е. существует сумма ряда Фурье

;

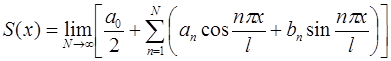2. Сумма ряда Фурье 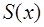равна функции 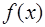в точках 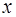ее непрерывности 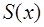= 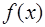и равна среднему арифметическому пределов функции 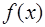слева и справа в точках 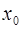разрыва функции, т.е.:

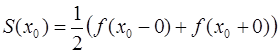
Поскольку, для точек непрерывности 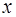функции 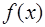можно записать 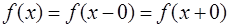, то в общем случае:

.

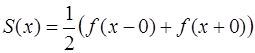Таким образом, для тригонометрического ряда Фурье функции 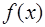имеем:

,

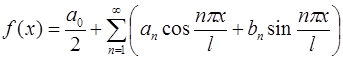где коэффициенты 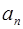и 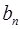определяются по формулам:

.

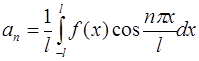
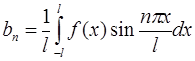Если принять, что период функции 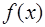равен 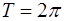, т.е. 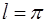, то расчетные формулы значительно упрощаются:

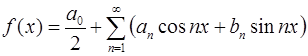
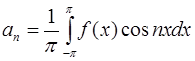
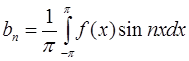
где 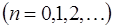.