Методы расчета надежности
Параллельная или последовательная структура надежности сложной системы дает представление о связи между надежностью системы и надежностью его элементов.
Под структурной схемой надежности понимается наглядное представление (графическое или в виде логических уравнении) элементов системы, позволяющие однозначно определить состояния системы (работоспособные или неработоспособные) по состоянию ее элементов.
При составлении структурной схемы надежности элементы системы могут соединяться последовательно (основное соединение), параллельно (резервное соединение) и смешанно. В последовательную цепочку соединяются такие элементы, отказ каждого из которых приводит к отказу системы. Поскольку при последовательном соединении элементов (рис. 17.1) работоспособное состояние системы имеет место при совпадений работоспособных состояний всех элементов, то вероятность этого состояния системы определяется произведением вероятностей работоспособных состояний всех элементов.
 |
Рисунок 17.1. Последовательное соединение
Если система состоит из n последовательно включенных элементов, то при вероятности безотказной работы каждого из элементов pi (t) вероятность безотказной работы системы Pc(t) определяется формулой
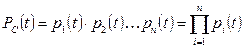 (17.1)
(17.1)
Если отказ системы возникает при отказе всех элементов, то такие элементы соединяют параллельно. При параллельном включении n элементов, вероятность отказа Qc(t) и вероятность безотказной работы Pc(t) этой системы определяется
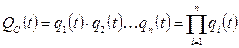 (17.2)
(17.2)
Pc(t)=1- 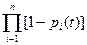 (17.3)
(17.3)
где qi(t) = 1 – pi(t) вероятность отказа i-го элемента.
Если структурная схема надежности системы состоит из последовательно и параллельно соединенных элементов, то расчет ее надежности может быть произведен с использованием выше приведенных формул.
Чтобы определить другие показатели надежности, требуется знать законы распределения времени безотказной работы элементов (наработки до отказа) системы. Поскольку на участке нормальной эксплуатации с удовлетворительной точностью в качестве закона распределения времени безотказной работы элементов может быть принят экспоненциальный, то при последовательном соединении элементов, если 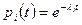 , выражение для вероятности безотказной работы системы примет следующий вид
, выражение для вероятности безотказной работы системы примет следующий вид
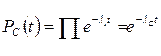 (17.4)
(17.4)
где 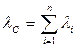 – параметр распределения ( интенсивность отказов).
– параметр распределения ( интенсивность отказов).
Таким образом, при основном соединении элементов, имеющих экспоненциальной закон распределения времени безотказной работы, этот закон для системы в целом также будет экспоненциальным. В соответствии с этим, другие показатели надежности системы определяется следующим образом.
Вероятность отказа 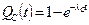 (17.5)
(17.5)
Частота отказа 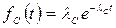 (17.6)
(17.6)
Средняя наработка до отказа Tср = 1/λc (17.7)
При параллельном соединении n – элементов, имеющих экспоненциальный закон распределения времени безотказной работы, вероятность отказа группы параллельно включенных элементов
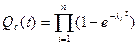 (17.8)
(17.8)
Если все элементы равнонадежны 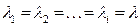 , то
, то
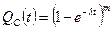 (17.9)
(17.9)
Вероятность безотказной работы
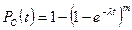 (17.10)
(17.10)
Таким образом, при резервном соединении элементов экспоненциальный закон распределения времени безотказной работы не сохраняется.
Во многих случаях рассмотренный выше способ расчета надежности не может быть использован, так как не всегда схема надежности содержит последовательно–параллельное соединение элементов. В этом случае можно сложную структуру заменить ее эквивалентной параллельно–последовательной структурой. К таким преобразованиям относится: а) преобразование с эквивалентной заменой треугольника на звезду и обратно; б) разложение сложной структуры по базовому элементу.
Преобразование с помощью эквивалентной замены треугольника звездой и обратно
Существо этого способа заключается в том, что узел сложной конфигурации заменяется на узел другой, более простой конфигурации, но при этом подбираются такие характеристики нового узла, чтобы показатели надежности преобразуемой цепи сохранялись прежними.
Пусть, например, требуется заменить треугольник звездой (рис. 17.2) при условии, что вероятность отказа элемента a равна q13,элемента b равна q12, элемента c равна q23.
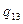

 1 3 1 3
1 3 1 3
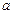
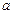
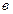
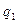
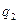
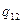
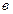
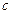
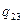
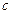
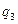
2 2
Рисунок 17.2. Преобразование треугольник – звезда.
Переход к соединению звездой не должен изменять надежность цепей 1 – 2, 1 – 3 и 2 – 3. Поэтому значения вероятностей отказов элементов звезды q1, q2 и q3 должны удовлетворять следующим равенствам
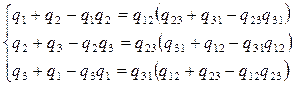
Если пренебречь произведениями вида qiqj и qiqjqk, то в результате решения системы уравнения можно записать
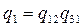 ;
; 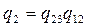 ;
; 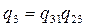 ; (17.11)
; (17.11)
Для обратного преобразования звезды в треугольник
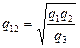 ;
; 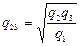 ;
; 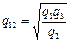 ; (17.12)
; (17.12)
Разложение сложной структуры по базовому элементу.
Этот способ преобразования сложных структурных схем основан на использовании теоремы о сумме вероятностей несовместных событий. В сложной структуре выбирают базовый элемент (или группу базовых элементов) и делаются следующие допущения:
1) базовый элемент находится в работоспособном состоянии (сигнал через него проходит)
2) базовый элемент находится в отказовом состоянии (сигнал через него не проходит)
Для этих случаев, представляющих собой два несовместных события, исходная структурная схема преобразовывается в две новые схемы. В первой из них вместо базового элемента ставится короткое замыкание цепи, а во второй – разрыв. Вероятности безотказной работы каждой из полученных простых структур вычисляются и умножаются: первая – на вероятность безотказного состояния базового элемента, вторая – на вероятность отказа базового элемента. Полученные произведения складываются. Сумма равна искомой вероятности безотказной работы сложной структуры.
Литература осн. 1 [63 – 73], осн. 2 [50 – 55]
Контрольные вопросы
1. Правило состояния последовательно–параллельной структуры расчета надежности.
2. Правила преобразования сложной структуры произвольной конфигурации к параллельно – последовательной структуре.
3. Определения вероятности безотказной работы системы при параллельном и последовательном соединений элементов этой системы.
4. Основные этапы расчета метода разложения сложной структуры относительно базового элемента
Метод перебора состояния
Расчету надежности любой системы независимо от используемого метода предшествует определение двух непересекающихся множеств состоянии элементов, соответствующих работоспособному и неработоспособным состояниям системы. Каждое из этих состояний характеризуется набором элементов, находящихся в работоспособном и неработоспособном состояниях. Поскольку при независимых отказах вероятность каждого из состояния определяется произведением вероятности нахождения элементов соответствующих состояниях, то при числе работоспособных состояний системы равном m, вероятность работоспособного состояния системы определяется следующим образом
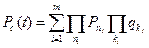 (17.13)
(17.13)
Вероятность отказа
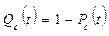 (17.14)
(17.14)
где m - общее число работоспособных состояний, Pn – вероятность безотказной работы, Qk – вероятность отказа, ni – число исправных элементов в j-том состоянии, kj – число отказавших элементов в 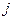 -том состоянии.
-том состоянии.
Применение этого метода покажем на типовом примере расчета, структурная схема которого изображена на рисунке 17.3.
| |
 |
Рисунок 17.3. Структурная схема надежности
Таблица 17.1
| A) Номер состояния | B) Состояния элементов | C) Вероятность состояний | |
| D) 1 элемент | E) 2 элемент | ||
| F) 1 G) 2 H) 3 | I) + J) - K) + | L) + M) + N) - | O) 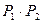 P) P) 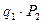 Q) Q) 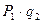 |
Для данного примера, вероятность безотказной работы системы равна
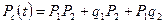 .
.
Из рассмотренного примера видно, что при сложной структуре применение метода перебора состояний сопряжено с громоздкими выкладками.
Метод минимальных путей и минимальных сечений
В ряде случаев для анализа надежности сложной системы бывает достаточным определить граничные оценки надежности сверху и снизу. При оценке вероятностей безотказной работы сверху определяют минимальные наборы работоспособных элементов (путей), обеспечивающих работоспособное состояние системы. При формировании пути, считая, что все элементы находятся в неработоспособном состоянии, последовательным переводом элементов в работоспособное состояние производят подбор вариантов соединений элементов, обеспечивающих наличие цепи. Набор элементов образует минимальный путь, если исключение (отказ) любого элемента из набора приводит к отказу пути. Из этого вытекает, что в пределах одного пути элементы находятся в основном соединении, а сами пути включается параллельно.
При оценке вероятности безотказной работы снизу определяют минимальные сечения. При определении минимальных сечении осуществляется подбор минимального числа элементов, перевод которых из работоспособного состояния в неработоспособное вызывает отказ системы. При правильном подборе элементов сечения возвращения любого из элементов в работоспособное состояние восстанавливает работоспособное состояние системы. Поскольку отказ каждого из сечений вызывает отказ системы, то сами сечения соединяются последовательно, а в пределах каждого сечения элементы соединяются параллельно, так как для работы системы достаточно наличия работоспособного состояния любого из элементов сечения.
У системы произвольной структуры может быть несколько минимальных сечений и путей. В частности, последовательное из 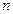 элементов имеет
элементов имеет 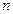 минимальных сечении, проходящий через каждый элемент и всего один минимальный путь. Параллельное соединение из
минимальных сечении, проходящий через каждый элемент и всего один минимальный путь. Параллельное соединение из 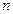 -элементов имеет
-элементов имеет 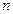 минимальных путей, проходящих через каждый элемент, и всего одно минимальное сечение.
минимальных путей, проходящих через каждый элемент, и всего одно минимальное сечение.
Таким образом, при составлении минимальных путей и сечений любая система преобразуется в структуру с параллельно-последовательным или последовательно-параллельным соединением элементов.
Логико-вероятностный расчет надежности.
Теоретической основой этого метода является математическая логика (булева алгебра), которая оперирует с логическими выражениями, имеющими значения “истина (1)” или “ложь (0)”. Логические выражения 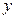 являются функциями логических переменных
являются функциями логических переменных 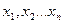 , каждая из которых также имеет значения 0 или1. Из
, каждая из которых также имеет значения 0 или1. Из 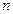 -переменных может быть образовано
-переменных может быть образовано 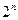 наборов и
наборов и 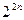 логических функции. Логические функции образуются с помощью трех операций: логического отрицания (
логических функции. Логические функции образуются с помощью трех операций: логического отрицания ( 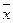 ), сложения (конъюнкция И), обозначаемого знаком V, и умножения (дизъюнкция, ИЛИ), обозначаемого
), сложения (конъюнкция И), обозначаемого знаком V, и умножения (дизъюнкция, ИЛИ), обозначаемого 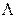 .
.
Логические функции, которые применительно к задачам надежности принято называть функциями работоспособности (надежности), могут задаваться в словесной форме, таблицами истинности, алгебраическими выражениями или графиками.
Для преобразования алгебраических выражений используются следующие тождества и законы математической логики.
Операция ИЛИ Операция И
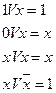
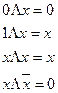
Закон коммутативности: 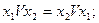
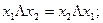
Закон ассоциативности: 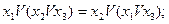
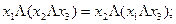
Закон дистрибутивности: 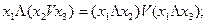
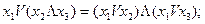
Закон дуальности (инверсии, Де-Моргана): 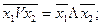
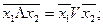
Закон поглощения: 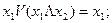
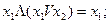
Для записи функции работоспособности в алгебраической форме используется одно из следующих выражений:
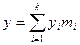 (совершенная дизъюнктивная нормальная форма СДНФ) или
(совершенная дизъюнктивная нормальная форма СДНФ) или
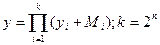 (совершенная конъюнктивная нормальная форма СКНФ) (17.15)
(совершенная конъюнктивная нормальная форма СКНФ) (17.15)
где 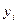 – значение функции работоспособности для соответствующей строки, 0 или 1;
– значение функции работоспособности для соответствующей строки, 0 или 1; 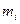 – конъюнкция набора элементов
– конъюнкция набора элементов 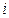 -той строки;
-той строки; 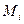 - дизъюнкция элементов
- дизъюнкция элементов 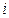 -той строки.
-той строки.
В качестве примера рассмотрим работоспособность системы, состоящей из трех элементов и заданной с таблицей истинности (таблица 17.2).
Таблица истинности Таблица 17.2
| R) x1 | S) x2 | T) x3 | U) x4 |
| V) 0 W) 1 X) 0 Y) 0 Z) 1 AA) 1 BB) 0 CC) 1 | DD) 0 EE) 0 FF) 1 GG) 0 HH) 1 II) 0 JJ) 1 KK) 1 | LL) 0 MM) 0 NN) 0 OO) 1 PP) 0 QQ) 1 RR) 1 SS) 1 | TT) 0 UU) 0 VV) 0 WW) 0 XX) 1 YY) 1 ZZ) 1 AAA) 1 |
СДНФ
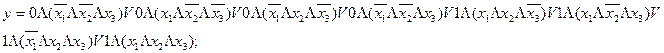 СКНФ
СКНФ
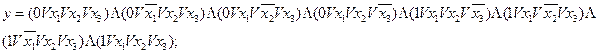
При расчете выбирают ту форму записи, которой соответствует меньшее число членов. При числе переменных более трех таблицы истинности становятся громоздкими и непосредственная минимизация функции работоспособности становится затруднительной. Для снижения размерности задачи выполняют декомпозицию функции работоспособности, опирающуюся на теорему разложения математической логики.
Разложение функции можно производить относительно любой из переменных
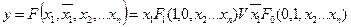 (17.16)
(17.16)
Переход от алгебраической формы записи работоспособности к вероятностной (арифметизация функции работоспособности), определяющей вероятность истинности этой функции, осуществляется простой заменой 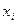 на
на 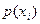 , если
, если 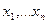 независимы и несовместны, т.е.
независимы и несовместны, т.е.
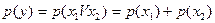 или
или
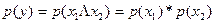 . (17.17)
. (17.17)
Если события 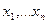 являются совместными, то при переходе к вероятностной форме используется следующая формула:
являются совместными, то при переходе к вероятностной форме используется следующая формула:
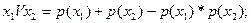 (17.18)
(17.18)
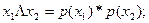 (17.19)
(17.19)
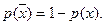 (17.20)
(17.20)
Рассмотренный метод анализа надежности применим к системам, элементы которых могут находится только в двух состояниях: работоспособности и неработоспособности.
Литература осн 1 [71-79], осн. 2 [48-50].
Контрольные вопросы
1. Сущность метода перебора состоянии.
2. Правило составления минимальных путей
3. Правило составления минимальных сечении
4. Основное тождество и законы математической логики
5. Сущность метода логико-вероятностного расчета
Метод основанный на составлении графа переходов чаще применяется тогда, когда производится расчет системы с учетом отказа и восстановления.
Система может находиться в двух состояниях: 1) работоспособном 2) отказовом.
Если интенсивность перехода в состояние отказа 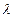 , а в работоспособное
, а в работоспособное 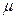 , то расчет надежности граф-переходов производится следующим образом:
, то расчет надежности граф-переходов производится следующим образом:
1) Составление граф-переходов, т. е. графическое представление переходов системы в различные состояния.
2) Записать уравнения непосредственно по графу состояния
Существует следующее правило, позволяющее записывать уравнения непосредственно по графу состояния:
1) В левой части уравнения записать dPk /dt, где Pk – вероятность k-го состояния.
2) В правой части уравнения записать столько членов, сколько стрелок связано с данным состоянием. Каждый член представляет собой произведение интенсивности перехода на вероятность того состояние, из которого происходит переход (исходит стрелка). При этом выходящей стрелочке соответствует знак минус, а входящей- знак плюс. Проверка правильности составления системы дифференциальных уравнений является равенство нулю суммы правых частей уравнений.
3) Решение системы дифференциальных уравнений.
При составлении граф переходов, каждая из вершин соответствует одному из состояний системы, а ориентация ребер определяется направлением перехода.
На рисунке 17.4 дан пример графа переходов. Система может находиться в двух состояниях: работоспособном 1 и отказа 2.
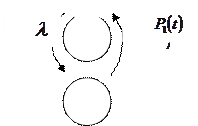
Р2(t)
Рисунок 17.4 Пример графа переходов
Согласно правилу запишем систему дифференциальных уравнений
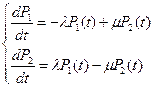 (17.21)
(17.21)
где 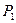 и
и 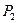 - вероятности работоспособного и отказового состояния, λ и μ – интенсивности перехода в состояния отказа и работоспособности.
- вероятности работоспособного и отказового состояния, λ и μ – интенсивности перехода в состояния отказа и работоспособности.
Поскольку система дифференциальных уравнении является линейно зависима, то для определения P1 и P2 используется дополнительное уравнение.
Если система может находится только в двух состояниях (например, восстановления и работы), то снижение вероятности одного состояния приводит к соответствующему увеличению вероятности другого состояния. Поэтому для любого момента времени выполняется 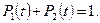 Для определения
Для определения 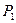 и
и 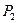 используется одно из уравнении системы дифференциальных уравнении и последнее соотношение.
используется одно из уравнении системы дифференциальных уравнении и последнее соотношение.
Следует отметить, что решение системы дифференциальных уравнении весьма трудоемкое, поэтому для облегчения расчета применяют следующие приемы расчета. При существующих в практике соотношениях λ и μ наступает сравнительно быстро период установившегося режима. При установившемся режиме вероятности состояния системы становятся постоянными ( 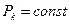 ). Это дает возможность принять при расчетах значения dPk/dt = 0. Тогда система дифференциальных уравнений становится системой алгебраических уравнении.
). Это дает возможность принять при расчетах значения dPk/dt = 0. Тогда система дифференциальных уравнений становится системой алгебраических уравнении.
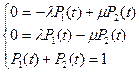 (17.22)
(17.22)
Для облегчения расчетов можно воспользоваться следующим правилом: если состояния заданы графом, имеющим вид, представленный на рисунке 17.5, тогда расчет надежности следует проводить в такой последовательности:
1) Записать уравнение состоянии для каждого состояния по правилу: в левой части написать нуль, в правой части столько членов, сколько стрелочек связано с данным состоянием (каждой стрелочке должно соответствовать слагаемое, представляющий собой произведение интенсивности переходов на вероятность того состояния, из которого происходит переход; выходящей стрелочке соответствует знак минус, входящей плюс).
2) Вероятности каждого из состояний определяются выражениями:
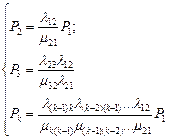 (17.23)
(17.23)
Запись для вероятности 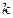 -го состояния следует читать так: вероятность
-го состояния следует читать так: вероятность 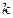 -го состояния равна произведению коэффициента на вероятность первого состояния
-го состояния равна произведению коэффициента на вероятность первого состояния 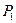 . Коэффициент равен дроби, числитель которой произведение интенсивностей отказов, стоящих над стрелочками, идущими вправо до
. Коэффициент равен дроби, числитель которой произведение интенсивностей отказов, стоящих над стрелочками, идущими вправо до 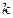 -го состояния, а знаменатель – произведение интенсивностей восстановлений, стоящих над стрелочками, идущими влево от
-го состояния, а знаменатель – произведение интенсивностей восстановлений, стоящих над стрелочками, идущими влево от 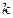 -го состояния до первого.
-го состояния до первого.
Вероятность первого состояния (все части системы исправны)
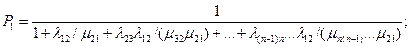 (17.24)
(17.24)
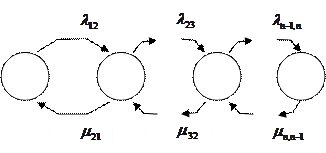 |
Рисунок 17.5 Граф переходов с учетом восстановления
При анализе надежности восстанавливаемых систем с непрерывным временем возникает две группы задач. Первая связана с определением функции и коэффициентов готовности и коэффициента простоя, а также параметра потока отказов. Вторая – с расчетом вероятности безотказной работы и средней наработкой до отказа.
Поскольку функция готовности 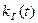 определяет вероятность нахождения системы в работоспособном состоянии в момент времени
определяет вероятность нахождения системы в работоспособном состоянии в момент времени 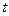 , то
, то
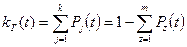 , (17.25)
, (17.25)
где 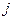 и
и 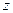 - работоспособные и неработоспособные состояния системы.
- работоспособные и неработоспособные состояния системы.
Функция простоя
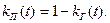 (17.26)
(17.26)
Для определения коэффициента готовности 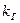 может быть применено несколько приемов. Один из них основан на непосредственном расчете предела
может быть применено несколько приемов. Один из них основан на непосредственном расчете предела 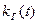 при
при 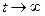 . Коэффициент готовности можно рассчитать по системе дифференциальных уравнений путем приравнивания нулю
. Коэффициент готовности можно рассчитать по системе дифференциальных уравнений путем приравнивания нулю 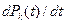 и решения системы алгебраических уравнений относительно всех работоспособных состоянии системы. Так, для предыдущего примера системы с двумя состояниями алгебраические уравнения для расчета
и решения системы алгебраических уравнений относительно всех работоспособных состоянии системы. Так, для предыдущего примера системы с двумя состояниями алгебраические уравнения для расчета 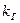 имеет вид:
имеет вид:
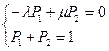 (17.27)
(17.27)
откуда 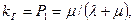 где
где 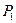 - вероятность работоспособного состояния системы.
- вероятность работоспособного состояния системы.
При решении второй группы задач в системе дифференциальных уравнений исключаются члены, содержащие в качестве сомножителей интенсивности выхода из поглощающего состояния (состояния восстановления системы являются поглощающими), т.е. интенсивности восстановления приравниваются к нулю. В этом случае вероятность безотказной работы
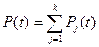 (17.28)
(17.28)
где k – все работоспособные состояния системы.
Среднее время безотказной работы рассчитывается как 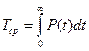 .
.
Литература: осн. 1 [131-139], осн. 2 [58-68].
Контрольные вопросы
1) Правило составления уравнений, определяющих вероятности состояний изделия, при использовании графа состояний.
2) Инженерные методы определения вероятностей состояний системы по виду графа состояний.
3) Как определяется функция готовности и коэффициент готовности?
4 Как определяется среднее время безотказной работы системы?
