Классические методы расчета надежности

К классическим методам относятся модели надежности с последовательным, параллельным, параллельно-последовательным соединениями элементов, их различные модификации.

Модель с последовательным соединением элементов (рис. 2.1). При расчетах надежности последовательным называется такое соединение элементов, при котором отказ хотя бы одного из них приводит к отказу всего соединения в целом. Последовательное соединение в указанном выше смысле не всегда совпадает с физическим последовательным соединением элементов. Отказы элементов предполагаются независимыми, то есть отказ любой группы элементов никак не влияет на вероятностные характеристики остальных элементов. Элемент понимается как один из самостоятельных участков последовательного соединения.

В данном случае вероятность безотказной работы системы можно рассчитать по формуле:

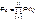
где Р_с – вероятность безотказной работы системы; Р_i(t) – вероятность безотказной работы i-го элемента системы

Модель с параллельным соединением элементов (рис. 2.2). При расчетах надежности параллельным (резервным) называется такое соединение элементов, при котором отказ всего соединения происходит при отказе всех элементов системы (элементы дублируют друг друга).

В этом случае показатель надежности системы P_c определяется через вероятности отказа элементов q₁, q₂, …, q_n, которые связаны с вероятностью безотказной работы соотношениями вида

q_i(t) = 1 – P_i(t)

Вероятность отказа всей системы равна:

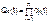
Тогда вероятность безотказной работы системы с параллельным соединением элементов q₁, q₂, …, q_n имеет вид

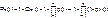
Модель с параллельно-последовательным соединением элементов. При расчетах надежности параллельно-последовательным называется такое соединение элементов, при котором можно составить структурные схемы участков как с последовательным, так и с паралелльным соединением элементов (рис. 2.3).

Для системы вначале рассчитывается вероятность безотказной работы участка 23:

P₂₃ = 1 - (1 - P₂(t))×(1 – P₃(t)),

затем – участка 123:

P₁₂₃(t) = P₁(t)×P₂₃(t) = P₁(t)×(1 – (1 – P₂(t))×(1 – P₃(t))).

Итоговая расчетная формула имеет вид

P_с(t) = 1 – (1 – P₁₂₃(t))×(1 – P₄(t)).

Модели несводимые к параллельно-последовательным соединениям. К данному классу относятся системы с мостовыми и еще более сложными соединениями элементов (рис. 2.4).

Система является работоспособной, если работоспособны элементы:

- 1,3 ;

- 2,4;

- ……….

- 1,5,4;

- 2,3,5;

Надежность систем данного класса целесообразно оценивать по логико-вероятностному методу, используя аппарат алгебры логики (см. раздел 2.3).

Модель с использованием марковских процессов. Модель задается в виде состояний, в которых система может находиться, и возможных переходов из одного состояния в другое (рис. 2.5).

При представлении ИС с помощью данной модели используется теория марковских процессов в том случае, если нахождение системы не зависит от того, в каком состоянии находилась ИС в прошлом.

Вероятностный граф состояний системы имеет следующие состояния:

1. Работают оба элемента системы.

2. Отказ одного из элементов.

3. Отказ двух элементов.

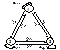
Рис. 2.5. Вероятностный граф состояний системы

Если заданы вероятности перехода системы из состояния iв состояние j b_ij, то можно определить вероятности нахождения системы в i-м состоянии P_i(t), а значит и показатели надежности, составляя и решая уравнение Колмогорова – Смирнова.

Производная от вероятности нахождения системы в i-том состоянии равна алгебраической сумме произведений интенсивностей перехода на вероятности соответствующих состояний. Тем произведениям, которым соответствуют уходящие из данного состояния стрелки, приписывают знак "-", а входящим – "+".

Таким образом, для данного примера системы имеем:

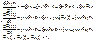
Решив систему уравнений (2.1), мы определим вероятности нахождения системы в i-м состоянии P_i(t).

Функция вероятности безотказной работы системы в данном случае равна вероятности нахождения системы в 1-м состоянии:

P_c(t) = P₁(t).