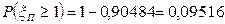Биномиальное распределение ДСВ
Так называется распределение вероятностей ДСВ , реализующее схему повторных испытаний. Пусть в результате опыта событие А появляется с вероятностью Р(А)=р.Обозначим 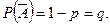 Если производится n одинаковых опытов или один опыт повторяется n раз, то вводится случайная величина
Если производится n одинаковых опытов или один опыт повторяется n раз, то вводится случайная величина 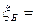 (число появлений события А в n опытах). Ясно, что такая ДСВ принимает значения 0,1,2,3…., n, а соответствующие вероятности
(число появлений события А в n опытах). Ясно, что такая ДСВ принимает значения 0,1,2,3…., n, а соответствующие вероятности 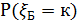 вычисляются по формуле Бернулли
вычисляются по формуле Бернулли 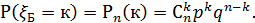 Распределение такой ДСВ и называется биномиальным, что подчёркивается индексом в обозначении
Распределение такой ДСВ и называется биномиальным, что подчёркивается индексом в обозначении 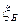 . Её ряд распределения имеет вид
. Её ряд распределения имеет вид
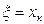 | … | К | … | n | |||
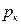 | 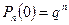 | 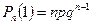 | 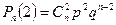 | … | 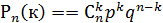 | … | 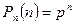 |
Отметим простейшие свойства распределения.
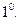 Хорошо известна формула бинома Ньютона
Хорошо известна формула бинома Ньютона
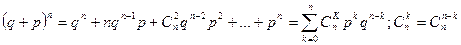 ,
, 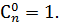 (24)
(24)
Формула справедлива при любых q и p. Если p и q – указанные выше вероятности, то p + q=1 и слагаемые формулы бинома Ньютона являются вероятностями ряда распределения. Собственно, и название биномиального распределения связано именно с биномом Ньютона.
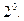 Числовые характеристики биномиального распределения.
Числовые характеристики биномиального распределения.
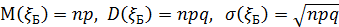
Пример 39. На поле 5 тракторов. Надёжность (т.е. вероятность безотказной работы) каждого трактора равна 0,8. Составить ряд и функцию распределения числа тракторов, работающих одновременно. Найти среднее число исправных тракторов. Вычислить вероятность того, что число исправных тракторов не менее трёх.
Решение. Обозначив событие А = {безотказная работа одного трактора}, по условию задачи имеем Р(А) = 0,8=р, 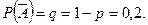 Вводим СВ
Вводим СВ 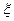 = (число тракторов, работающих одновременно) и видим, что
= (число тракторов, работающих одновременно) и видим, что 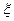 есть
есть 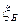 , т.е. распределена по биномиальному закону при n = 5. Её ряд распределения и функция распределения выглядят следующим образом
, т.е. распределена по биномиальному закону при n = 5. Её ряд распределения и функция распределения выглядят следующим образом
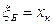 | ||||||
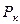 | 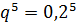 = 0,00032 = 0,00032 | 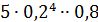 = 0,0064 = 0,0064 | 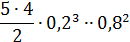 = 0,0512 = 0,0512 | 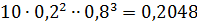 | 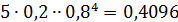 | 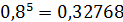 |
Контроль: 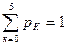
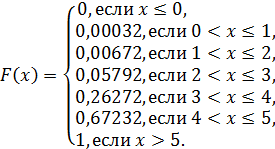
Вычисляем числовые характеристики:
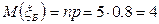 ;
; 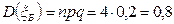 ,
, 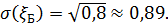
Вероятность того, что число исправных тракторов не менее трёх вычислим по ряду распределения:
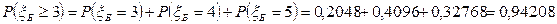
16.2. Распределение Пуассона.
Обычно рассматривается некоторый временной промежуток, в течение которого наблюдают появление события А и вводится ДСВ 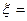 (число появлений события А). Если вероятность
(число появлений события А). Если вероятность 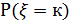 того, что число появлений события А вычисляется по формуле Пуассона, то и ДСВ называется распределённой по закону Пуассона и обозначается
того, что число появлений события А вычисляется по формуле Пуассона, то и ДСВ называется распределённой по закону Пуассона и обозначается 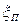 . Таким образом,
. Таким образом,
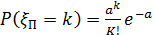 (25)
(25)
Её ряд распределения выглядит следующим образом.
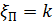 | … | к | … | ||||
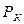 | 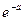 | 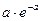 | 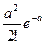 | 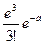 | … | 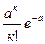 | … |
Как видим, 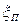 принимает бесконечное (счётное) множество значений. Отметим простейшие свойства распределения Пуассона.
принимает бесконечное (счётное) множество значений. Отметим простейшие свойства распределения Пуассона.
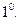 Легко убедиться в том, что выполняется основное требование ряда распределения:
Легко убедиться в том, что выполняется основное требование ряда распределения: 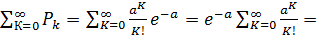
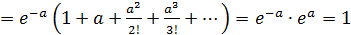 - выражение в скобке есть разложение
- выражение в скобке есть разложение 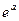 в ряд Маклорена.
в ряд Маклорена.
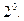 Числовые характеристики:
Числовые характеристики:
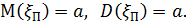
Отметим, что такое численное равенство матожидания и дисперсии справедливо лишь для закона Пуассона и на практике применяется для проверки правдоподобности гипотезы о том, что исследуемая случайная величина распределена по закону Пуассона.
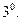 Закон Пуассона является предельным для биномиального:
Закон Пуассона является предельным для биномиального:
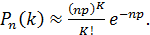
В силу того, что р – мало, а n – велико, закон Пуассона называется законом редких явлений. Он находит большое применение на практике. К закону Пуассона приводят число отказов сложной аппаратуры, число вызовов на телефонной станции за время t; число обрывов нити в прядильном цехе; число отказов для группы одновременно работающих автомобилей в течение заданного промежутка времени (или наработки); число аварий или ДТП; число дефектных изделий, попадающих в выборку из партии изделий; число клиентов, обращающихся на пункт обслуживания в единицу времени; количество запасных частей, забираемых со склада и многое другое.
Пример 40. Среднее число отказов радиоаппаратуры за 1000 часов работы равно 5. Определить вероятность отказа радиоаппратуры за 20 часов.
Решение. Если среднее число отказов радиоаппаратуры за 1000 часов равно 5, то за 20 часов среднее число отказов равно 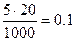 . Вводим ДСВ
. Вводим ДСВ 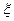 = (число отказов радиоаппаратуры за 20 часов), тогда
= (число отказов радиоаппаратуры за 20 часов), тогда 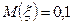 и будем считать, что
и будем считать, что 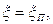 т.е. распределена по закону Пуассона. Тогда по условию задачи требуется найти вероятность
т.е. распределена по закону Пуассона. Тогда по условию задачи требуется найти вероятность 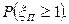
Легче всего эту вероятность посчитать через вероятность противоположного события: 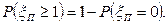 По таблицам распределения Пуассона при
По таблицам распределения Пуассона при 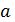 =0,1 получим
=0,1 получим 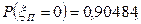 следовательно,
следовательно,