Кинематика вращательного движения абсолютно твёрдого тела. Угловая скорость и угловое ускорение, их связь с линейной скоростью и линейным ускорением точек вращающегося тела
Физика. Экзамен.
Кинематика материальной точки, Основная задача кинематики, три способа геометрического описания движения материальной точки. Кинематическое уравнение движения материальной точки.
Кинематика – раздел механики, изучающий механическое движение без учёта масс тел и действующих на них сил.
Под материальной точкой понимают обладающее массой тело, размерами и формой которого в конкретной ситуации можно пренебречь.
Основная задача кинематики:
Определение положения тела в пространстве в произвольный момент времени.
Движение тела описывают относительно другого тела, принятого за тело отсчёта.
3 способа геометрического описания движения материальной точки:
1. Векторный. Положение точки по отношению к системе отсчёта определяется её радиус-вектором. Уравнение движения: 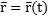 .
.
2. Координатный. Положение точки относительно системы отсчёта определяется 3мя координатами.
x=rx=r*cos(a)
y=ry=r*cos(b)
z=rz=r*cos(c)
3. Траекторный (естественный). Описывается с помощью траектории, по которой движется точка. S=S(t).
Кинематическое уравнение движения материальной точки.
X=x(t)
Y=y(t)
Z=Z(t)
Кинематические характеристики движения точки: скорость и ускорение. Нормальное и тангенциальное ускорение материальной точки.
Скорость и ускорение материальной точки – основные характеристики её движения.
Средняя скорость: 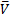 ср =
ср = 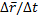
Путевая средняя скорость: Vср = 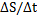
Мгновенная скорость: 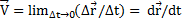
Скорость равна первой производной радиус-вектора по времени.
Модуль скорость равен корню из суммы квадратов проекций скорости на оси в прямоугольной системе координат.
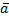 ср =
ср = 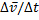
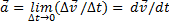
Ускорение равно первой производной скорости по времени.
При криволинейном движении ускорение может быть разбито на 2 составляющие:
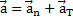
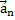 – нормальная составляющая ускорения. Отвечает за изменение скорости по направлению.
– нормальная составляющая ускорения. Отвечает за изменение скорости по направлению.
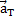 -- касательная составляющая ускорения. Отвечает за изменение скорости по модулю.
-- касательная составляющая ускорения. Отвечает за изменение скорости по модулю.
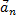 =dvn/dt=v*(d
=dvn/dt=v*(d 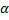 /dt)*(dS/dS)=v^2 * d
/dt)*(dS/dS)=v^2 * d 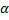 /dS;
/dS;
dS=R* d 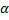
an=v^2/R
aT=dvT/dt=dv/dt
Кинематика вращательного движения абсолютно твёрдого тела. Угловая скорость и угловое ускорение, их связь с линейной скоростью и линейным ускорением точек вращающегося тела.
Вращательное движение – движение, при котором какие-либо две точки А и В остаются неподвижными. Прямая АВ – ось вращения. Все точки АТТ при вращении описывают окружности в плоскостях, перпендикулярных АВ и с центрами, лежащими на этой оси. При вращении тело имеет 1 степень свободы, а его положение определяется углом.
Угловая скорость — векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени.
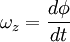
Существует связь между линейной и угловой скоростями:
V= 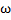 *R
*R
Угловое ускорение — физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.
При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно:
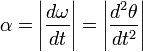
Существует связь между тангенциальным и угловым ускорениями:
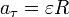
где R — радиус кривизны траектории точки в данный момент времени.
