Динамика вращательного движения абсолютно твёрдого тела. Момент силы относительно неподвижной точки и неподвижной оси вращения. Работа сил при вращении а.т.т
Момент 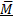 силы
силы 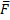 относительно неподвижной точки О есть векторная физическая величина, которая равна векторному произведению
относительно неподвижной точки О есть векторная физическая величина, которая равна векторному произведению 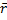 и
и 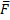
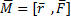
M=r*F*sinα
M=F*l (l-плечо силы)
Если на тело действует несколько сил, то результирующая будет равна алгебраической сумме:
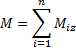
Работа сил при вращении:
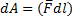 ;
;
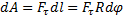 ;
;
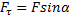 ;
;
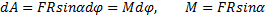
Динамика вращательного движения абсолютно твёрдого тела. Момент инерции тела. Кинетическая энергия вращения.
Момент инерции тела – скалярная физическая величина, равная произведению массы на квадрат расстояния до оси.
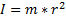
[I]=кг*м2
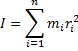
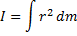
Кинетическая энергия вращательного движения:
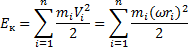
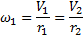
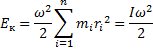
При плоском движении кинетическая энергия движущегося твердого тела равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, проходящей через центр масс тела и перпендикулярной плоскостям, в которых движутся все точки тела:
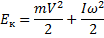
Динамика вращательного движения тела. Основной закон динамики вращательного движения тела относительно неподвижной оси вращения.
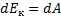
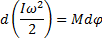
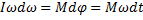
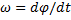 ⇒
⇒ 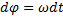
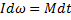
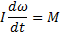
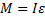
Основной закон:
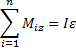
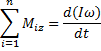
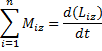
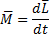
Динамика вращательного движения тела. Момент импульса, закон сохранения момента импульса.
Момент импульса L - характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Определяется векторным произведением ее радиус-вектора и импульса:
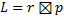
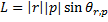
Где r - радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчета начала отсчёта, p - импульс частицы.
Для систем, совершающих вращение вокруг одной из осей симметрии справедливо соотношение:
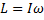
Закон сохранения момента импульса:
В замкнутой системе момент внешних сил равен 0, т.е. ∑Miz=0 ⇒ 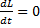 ⇒Lz=const.
⇒Lz=const.
Это фундаментальный закон природы. Он связан со свойством симметрии пространства, его изотропностью. Изотропность — одно из ключевых свойств пространства в классической механике. Пространство называется изотропным, если поворот системы отсчета на произвольный угол не приведет к изменению результатов измерений.
Гармонические колебания и их характеристики. Дифференциальное уравнение свободных колебаний.
Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса.
Основные характеристики: период колебаний, смещение точки от положения равновесия, амплитуда колебаний, начальная фаза.
Дифференциальное уравнение свободных колебаний:
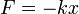
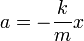
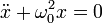
Решение: