Теорема о представлении любой булевой функции в виде СКНФ
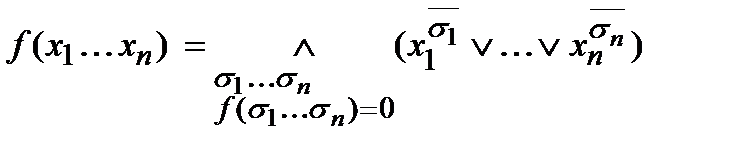
Пример:
| x1 | x2 | f |
| 0 | ||
| 1 | ||
| 1 |
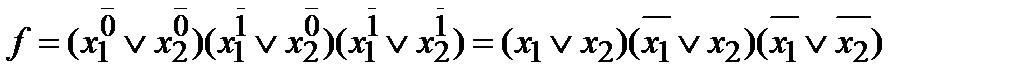
Доказательство : рассмотрим произвольный набор значений переменных 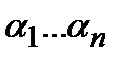 . Либо
. Либо 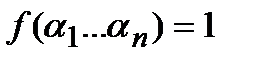 , либо
, либо 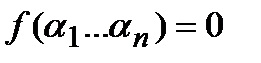 .
.
1) Левая часть равенства равна 1. Покажем, что и правая часть равна единице. Рассмотрим произвольный множитель правой части 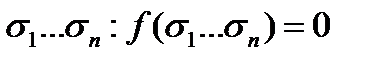 . Значение этого множителя на наборе
. Значение этого множителя на наборе 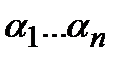 равно
равно 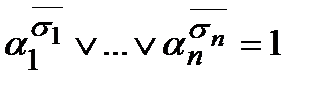 т.к. существует i такое, что
т.к. существует i такое, что 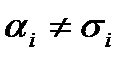 , что верно в силу того, что a - набор, на котором значение f (a) = 1, а s - набор, на котором значение f(s)= 0, то есть a и s - два различных набора, а поэтому есть компонента, в которой они отличаются.
, что верно в силу того, что a - набор, на котором значение f (a) = 1, а s - набор, на котором значение f(s)= 0, то есть a и s - два различных набора, а поэтому есть компонента, в которой они отличаются.
Поэтому 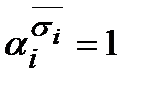 ; т.к.
; т.к. 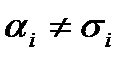 ,
, 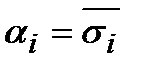 .
.
2) Пусть 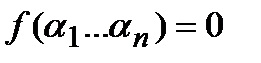 . Покажем, что и правая часть равна 0. Для этого достаточно показать, что существует множитель, который равен 0 на наборе a. Действительно, рассмотрим множитель соответствующий набору правой части
. Покажем, что и правая часть равна 0. Для этого достаточно показать, что существует множитель, который равен 0 на наборе a. Действительно, рассмотрим множитель соответствующий набору правой части 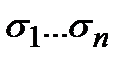 , который совпадает с набором
, который совпадает с набором 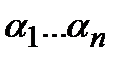 .
.
В силу того, что 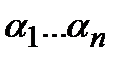 есть ноль функции, набор
есть ноль функции, набор 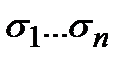 существует. Тогда значение рассматриваемого множителя на наборе a равно
существует. Тогда значение рассматриваемого множителя на наборе a равно 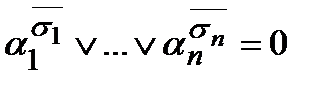
(т. к.  для всех i :
для всех i : 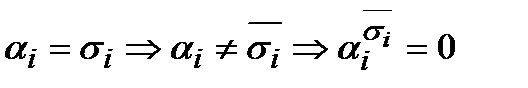 ). А так как существует множитель, равный 0, то и значение всей СКНФ = 0.
). А так как существует множитель, равный 0, то и значение всей СКНФ = 0.
Теорема о разложении булевой функции по первым k переменным .
Для любой булевой функции f(x1…xn) тождественно выполнено :
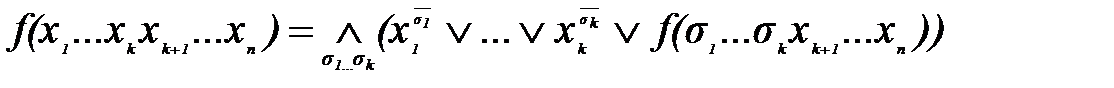
Доказательство. Рассмотрим произвольный набор 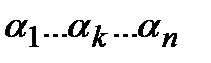 . Значение левой части есть
. Значение левой части есть 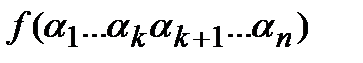 .
.
В правой части множитель, в котором 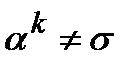 будет равен 1 в силу того, что
будет равен 1 в силу того, что 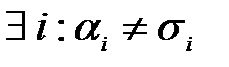 , тогда
, тогда 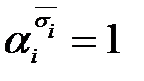 в силу того, что
в силу того, что 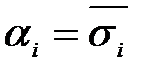 , а раз некоторое слагаемое равно 1 , вся элементарная дизъюнкция равна 1. Тогда остается один множитель
, а раз некоторое слагаемое равно 1 , вся элементарная дизъюнкция равна 1. Тогда остается один множитель 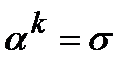 , который равен
, который равен
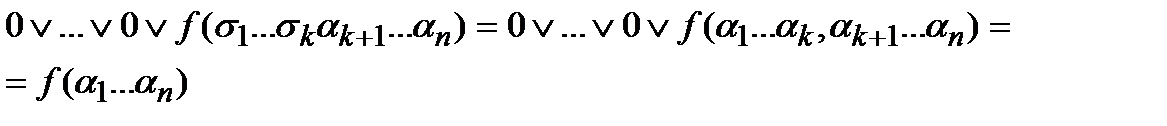
Тогда все произведение есть 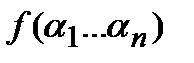 . Что и требовалось доказать.
. Что и требовалось доказать.
ЗамечаниеИспользуя понятие двойственности, можно показать справедливость предыдущих утверждений о КНФ непосредственным сведением к утверждениям о ДНФ. В разделе о суперпозиции функций будет приведено данное доказательство.
Определение : Полиномом Жегалкина называется сумма по модулю 2 (+) некоторого количества слагаемых, где каждое слагаемое есть элементарная конъюнкция переменных без отрицания.
Пример:
1+x1x2+x3+x1x4x5
Полином Жегалкина, не содержащий ни одного слагаемого, равен 0.
Далее будем рассматривать так называемые приведенные полиномы Жегалкина, т.е. полиномы, в которых все слагаемые различные конъюнкции.
Например 1+x1x2+x3+x1x4x5 (нет двух одинаковых слагаемых).
Если некоторые слагаемые повторяются, то используя правило x+x=0, нетрудно привести любой полином к приведенному виду.
Например x1x2+x3+x1x2+x1x4x5+x3=x1x4x5
Если слагаемое повторяется нечетное количество раз, то оставляем его в единственном экземпляре.
1.4 Утверждение о представлении двоичной функции в виде полинома Жегалкина .
Для любой булевой функции существует представление в виде полинома Жегалкина и это представление единственно.
Доказательство:
Пример 1:
| x1 | x2 | x3 | |
| 1 | |||
Первая часть теоремы следует из теоремы о представлении булевой функции в виде СДНФ. А именно рассмотрим для булевой функции ее СДНФ. Далее операцию  выразим через операцию
выразим через операцию  по правилу Де Моргана
по правилу Де Моргана 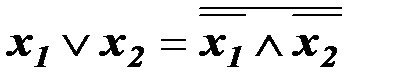 .
.
После чего операцию 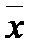 выразим через операцию
выразим через операцию 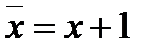 и приведем полученную формулу к нормальному виду полинома Жегалкина раскрыв скобки в полученном выражении, используя дистрибутивность конъюнкции по отношению к сумме по модулю два. Для функции из примера1 СДНФ имеет вид :
и приведем полученную формулу к нормальному виду полинома Жегалкина раскрыв скобки в полученном выражении, используя дистрибутивность конъюнкции по отношению к сумме по модулю два. Для функции из примера1 СДНФ имеет вид :
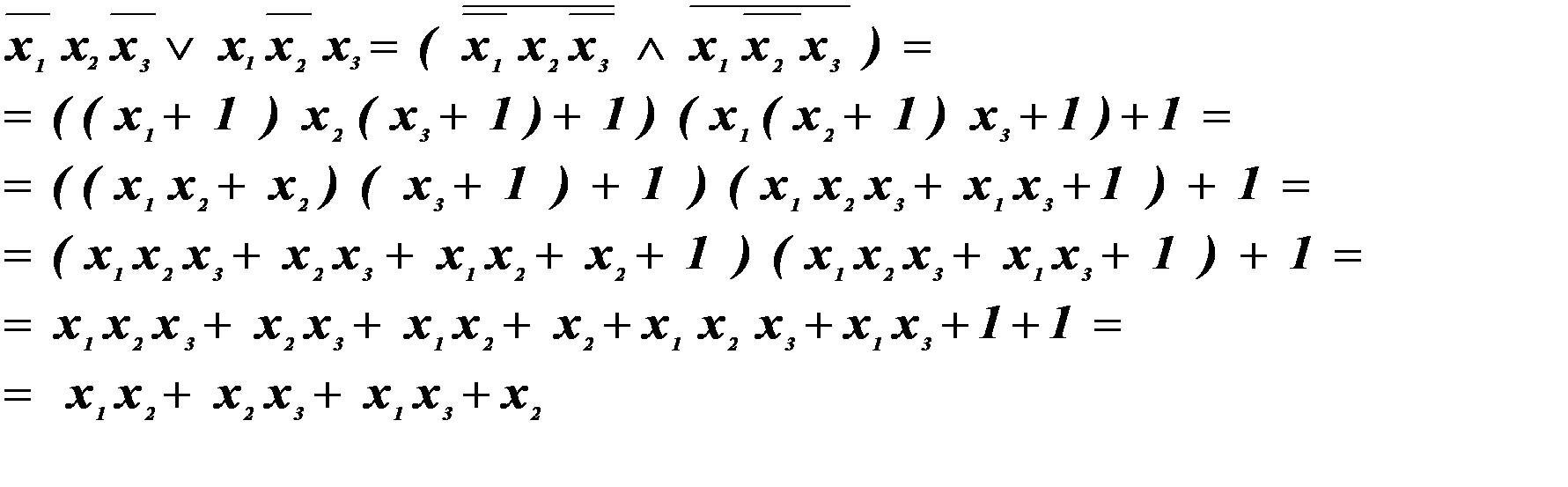
Покажем, что полученный полином единственен с точностью до перестановки слагаемых и множителей в слагаемых полинома.
Допустим противное : 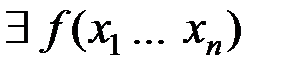 , которая имеет два различных полинома Жегалкина:
, которая имеет два различных полинома Жегалкина:
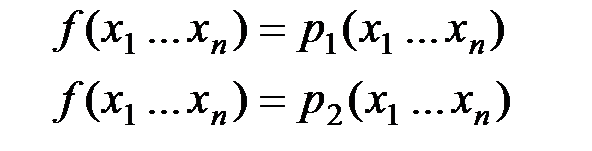
Из этих равенств следует,что
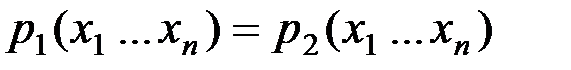
прибавим к обеим частям равенства 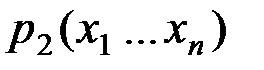 :
:
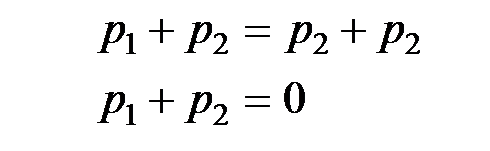
В силу того, что 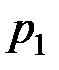 и
и 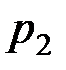 различные полиномы Жегалкина, либо в
различные полиномы Жегалкина, либо в 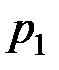 есть слагаемое, которого нет в
есть слагаемое, которого нет в 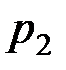 , либо наоборот. Поэтому приведенный полином
, либо наоборот. Поэтому приведенный полином 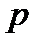 отличен по форме от нуля
отличен по форме от нуля 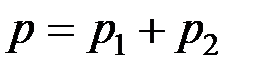 , т.е. в этом полиноме присутствуют слагаемые, не тождественно равные нулю, и полином тождественно равен константе ноль :
, т.е. в этом полиноме присутствуют слагаемые, не тождественно равные нулю, и полином тождественно равен константе ноль : 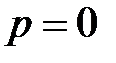 .
.
Далее рассмотрим слагаемое полинома 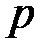 , содержащее наименьшее число переменных. Теперь рассмотрим набор значений переменных, в котором переменные данного слагаемого равны 1, а все остальные переменные равны 0. Тогда, нетрудно видеть, что значение
, содержащее наименьшее число переменных. Теперь рассмотрим набор значений переменных, в котором переменные данного слагаемого равны 1, а все остальные переменные равны 0. Тогда, нетрудно видеть, что значение 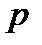 на таком наборе равно 1 (в полиноме будет ровно 1 только одно слагаемое с наименьшим числом переменных, остальные обязательно содержат нулевой множитель, поэтому равны 0), в то время как
на таком наборе равно 1 (в полиноме будет ровно 1 только одно слагаемое с наименьшим числом переменных, остальные обязательно содержат нулевой множитель, поэтому равны 0), в то время как 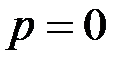 на всех наборах. Противоречие.
на всех наборах. Противоречие.
Упражнение: найдите полином Жегалкина следующих функций :
1) 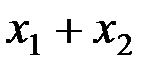 4)
4) 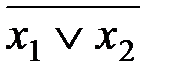
2) 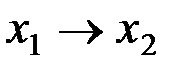 5)
5) 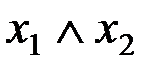
3) 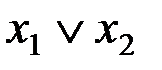 6)
6) 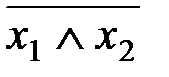
Упражнение
Покажите справедливость формулы для любой двоичной функции f справедливо разложение
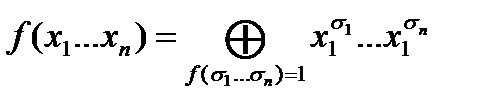 л
л
Т.е в формуле представления функции в виде СДНФ можно заменить логическое суммирование на суммирование по модуля 2.
Определение
Пусть 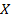 – конечное множество. Отношением на данном множестве будем называть любое подмножество его декартового произведения
– конечное множество. Отношением на данном множестве будем называть любое подмножество его декартового произведения 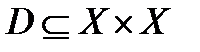 .
.
Рассмотрим декартово произведение 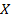 на себя:
на себя: 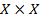 . Т.е. это множество всевозможных слов из двух букв в алфавите
. Т.е. это множество всевозможных слов из двух букв в алфавите 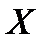 .
.
Определение
Отношением эквивалентности 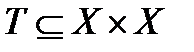 называется подмножество декартового произведения, которое удовлетворяет следующих трем свойствам:
называется подмножество декартового произведения, которое удовлетворяет следующих трем свойствам:
1. Рефлексивность. 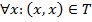 .
.
2. Симметричность. 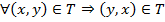 .
.
3. Транзитивность. 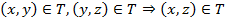 .
.
