Цикломатическая матрица
Цикл в графе можно обойти в одном из двух направлений: по часовой или против часовой стрелки. Направление, выбираемое для обхода цикла, определяет его ориентацию.
Рассмотрим дугу e с концевыми вершинами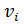 
к 
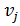и входит в цикл C. Будем говорить, что ориентация дуги e соответствует ориентации цикла, если вершина 
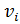встречается при обходе цикла C в направлении, указанном его ориентацией, раньше вершины 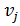. Цикломатическая матрица 
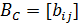графа G с m ребрами имеет m и столько строк, сколько циклов имеется в графе G. Элемент 
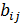определяется следующим образом :
Если граф ориентированный,
Если граф неориентированный,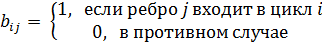 
Матрица Кирхгофа.
Дан простой граф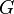 
с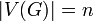 
вершинами. Тогда матрица Кирхгофа 
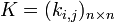данного графа будет определяться следующим образом:
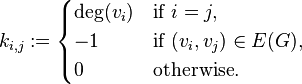
Также матрицу Кирхгофа можно определить как разность матриц
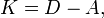
где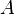 
— это матрица смежности данного графа, а 
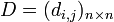— матрица, на главной диагонали которой степени вершин графа, а остальные элементы — нули:
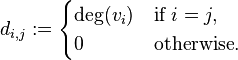
Если граф является взвешенным, то определение матрицы Кирхгофа обобщается. В этом случае элементами главной диагонали матрицы Кирхгофа будут суммы весов рёбер, инцидентных соответствующей вершине. Для смежных (связанных) вершин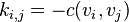 
, где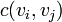 
— это вес (проводимость) ребра. Для различных несмежных (несвязанных) вершин полагается 
.
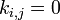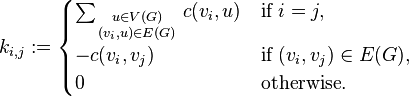
Для взвешенного графа матрица смежности 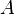записывается с учетом проводимостей ребер, а на главной диагонали матрицы 
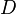будут суммы проводимостей ребер инцидентных соответствующим вершинам.
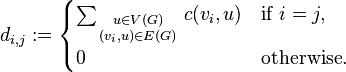
Пример матрицы Кирхгофа.
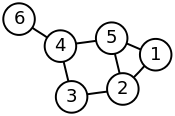
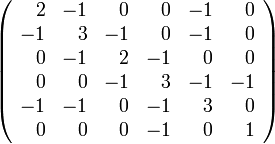
Специальные свойства графов.
Пусть G — произвольный (n,m)-граф с k компонентами связности. Если G — не лес, то в нем (его компонентах связности) существуют циклы. Рассмотрим какой-либо цикл и удалим из него некоторое ребро. При этом количество компонент связности не увеличится. Если после этого еще останутся циклы, то рассмотрим следующий из них и снова удалим какое-либо его ребро. Продолжим этот процесс до тех пор, пока не исчезнут все циклы. Полученный в результате подграф, который, очевидно, является лесом и имеет столько же компонент связности, как и исходный граф G, называется остовом графа G.
Теорема. Число ребер графа G, которые нужно удалить для получения остова, не зависит от способа удаления и равно m-n+k.
Теорема (Кирхгоф). Число остовов в связном графе G порядка n>=2 равно алгебраическому дополнению любого элемента матрицы Кирхгофа K(G) графа G.
Теорема. Орграф сильно связен, если в нем существует основной циклический маршрут.
Решение оптимизационных задач.
Алгоритм Дейкстры.
Алгоритм Дейкстры — алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко применяется в программировании и технологиях, например, его используют протоколы маршрутизации OSPF и IS-IS.
Алгоритм Дейкстры решает задачу о кратчайших путях из одной вершины для взвешенного ориентированного графа G = (V, E) с исходной вершиной s, в котором веса всех рёбер неотрицательны (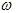 
(u, v) ≥ 0 для всех (u, v) 
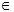E).
Пример решения задачи. Поиск ведется на данном графе (Рис 3.1). Веса соответствуют длине ребер.
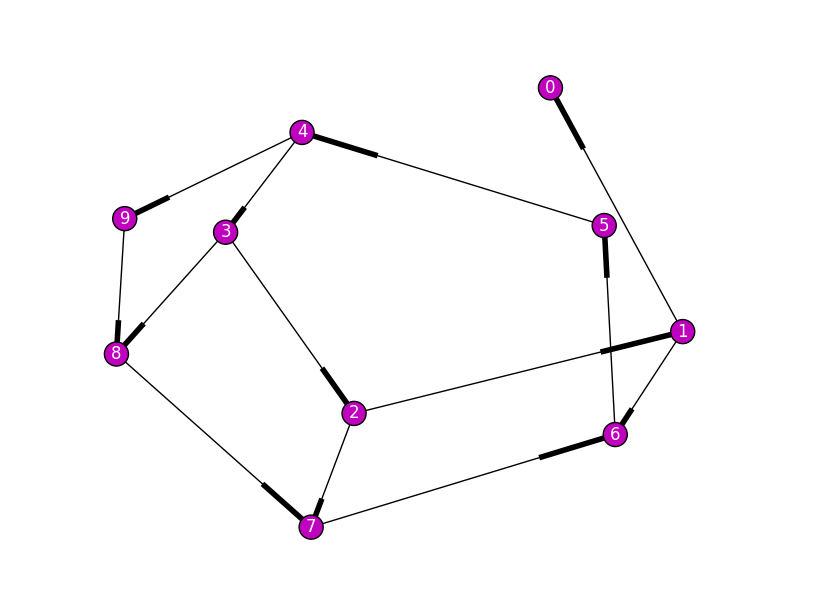Рис 3.1
Листинг 2.
import networkx as nx
import matplotlib.pyplot as plt
G = nx.DiGraph() #Объявляем орграф G
G.add_nodes_from(range(1, 7)) #Добавляем вершины из набора чисел(1..7)
for i in range(1,10):
G.add_edge(i, i-1) #Добавляем ребро, соединяющее вершину i с i-1
for i in range(1,10):
if(i+5<10):
G.add_edge(i, i+5, weight = i*0.5+2)#Устанавливаем веса на ребра
nx.draw(G, node_color = 'm', font_color = 'w')
plt.show()
print(nx.dijkstra_path(G, 2, 8)) #Поиск и вывод массива вершин
# Использование функции для нахождения маршрута. Поиск начинается с вершины 2 и идет до вершины 8.
Выходные данные:
[2, 1, 6, 5, 4, 3, 8]
Алгоритм поиска.
0. G – данный ориентированный граф с взвешенными ребрами. Требуется найти кратчайшие пути из вершины s во все остальные вершины графа G.
1. (Начало). Положить label(s) = 0, perm(s) = 1 и pred(s) = s. Для всех v <> s положить label(v) = ∞, perm(v) = 0, pred(v) = v.
2. Пусть i = 0 и u = s. (u – последняя из вершин с неизменной меткой. Теперь – это вершина s.)
3. (Вычисление label и изменение элементов массива pred). Положить i = i + 1. Выполнить для каждой вершины, кроме вершин с неизменной меткой, следующие действия: 1) Положить M = min{label(v), label(u) + w(u, v)}. 2) Если M<label(v), то положить label(v) = M и pred(v) = u.
4. (Выделение вершин ui.) Среди всех вершин, которые не помечены неизменной меткой, найти вершину w с наименьшей меткой. (Если таких вершин несколько, то выбор можно сделать произвольно.) Положить perm(w) = 1 и ui = w (ui = w, и она является последней вершиной с неизменной меткой.)
5. Если i < n – 1, то идти к шагу 3. Иначе halt. (Все кратчайшие пути найдены). Метки вершин представляют собой длины кратчайших путей. v, pred(v), pred(pred(v)), …, s есть вершины кратчайшего ориентированного s-v – пути.
Здесь label - это массив, в котором хранятся текущие метки вершин. Вершины становятся постоянно помеченными, когда они оказываются равными ui для какого-либо i. Мы используем массив perm, чтобы указать, какие вершины постоянно помечены. Если perm(v) = 1, то v является постоянно помеченной вершиной. Отметим, что в таком случае метка v равна d(s, v). Вначале perm(s) = 1 и perm(v) = 0 для всех v<>s.
Pred – массив указателей на вершины, из которых осуществлен переход в вершины с неизменной меткой, то v, pred(v), pred(pred(v)), …, s есть вершины, составляющие кратчайший ориентированный путь из s в v.
Данный алгоритм работает также для решения задачи коммивояжера.
Задача коммивояжера.
Задача коммивояжёра (англ. Travelling salesman problem, TSP) (коммивояжёр — странствующий торговец) — одна из самых известных задач комбинаторной оптимизации, заключающаяся в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с последующим возвратом в исходный город. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешёвый, совокупный критерий и тому подобное) и соответствующие матрицы расстояний, стоимости и тому подобного. Как правило, указывается, что маршрут должен проходить через каждый город только один раз — в таком случае выбор осуществляется среди гамильтоновых циклов.
Существует несколько частных случаев общей постановки задачи, в частности геометрическая задача коммивояжёра (также называемая планарной или евклидовой, когда матрица расстояний отражает расстояния между точками на плоскости), метрическая задача коммивояжёра (когда на матрице стоимостей выполняется неравенство треугольника), симметричная и асимметричная задачи коммивояжёра. Также существует обобщение задачи, так называемая обобщённая задача коммивояжёра.
Оптимизационная постановка задачи относится к классу NP-трудных задач, впрочем как и большинство её частных случаев. Версия «decision problem» (то есть такая, в которой ставится вопрос существует ли маршрут не длиннее, чем заданное значение k) относится к классу NP-полных задач. Задача коммивояжёра относится к числу трансвычислительных: уже при относительно небольшом числе городов (66 и более) она не может быть решена методом перебора вариантов никакими теоретически мыслимыми компьютерами за время, меньшее нескольких миллиардов лет.
Непременным условием и единственным смыслом задачи коммивояжёра является поиск самого выгодного пути. Для этого необходимо найти и описать все возможные пути при любом из вариантов способов поиска решения. Если мы не просчитали все пути в выбранном варианте решения, то мы не можем утверждать, что найденное решение самое выгодное. Что такое проверка решения? — это поиск ошибки в процессе решения или сверка полученного результата с заведомо правильным. Второй вариант временно отбрасываем, так как нет практического смысла в решении задачи, если уже есть решение (в свою очередь, использование ранее выполненного верного решения для части имеющейся задачи — способ уменьшить решение). В рамках данной работы не ставилось целью сравнение различных методов и способов решения, поэтому принимаем, что проверяющий также считает выбранный способ решения оптимальным и проверяет его на правильность. Что нужно сделать проверяющему? — повторить работу, проделанную при решении, в полном объёме для поиска ошибки на каждом этапе решения. Если будет найдена ошибка, то проверяющему будет необходимо продолжить процесс решения для поиска более выгодного маршрута. Таким образом, мы получаем, что проверка решения задачи коммивояжёра равна или больше самого решения.
Представление в виде графа.
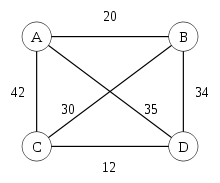
Рис. 3.2
Симметричная задача для четырёх городов.
Для возможности применения математического аппарата для решения проблемы, её следует представить в виде математической модели. Проблему коммивояжёра можно представить в виде модели на графе, то есть, используя вершины и ребра между ними. Таким образом, вершины графа соответствуют городам, а ребра (i, j) между вершинами i и j — пути сообщения между этими городами. Каждому ребру (i, j)>=0 можно сопоставить критерий выгодности маршрута, который можно понимать как, например, расстояние между городами, время или стоимость поездки. Маршрутом (также гамильтоновым маршрутом) называется маршрут на таком графе, в который входит по одному разу каждая вершина графа. Задача заключается в отыскании кратчайшего маршрута.
В целях упрощения задачи и гарантии существования маршрута, обычно считается, что модельный граф задачи является полностью связным, то есть, что между произвольной парой вершин существует ребро. В тех случаях, когда между отдельными городами не существует сообщения, этого можно достичь путем ввода рёбер с максимальной длиной. Из-за большой длины такое ребро никогда не попадет к оптимальному маршруту, если он существует.
В зависимости от того, какой критерий выгодности маршрута сопоставляется величине ребер, различают различные варианты задачи, важнейшими из которых являются симметричная и метрическая задачи.
Пример решения задачи коммивояжера на языке python на заданном графе (Рис. 3.2).
В листинге 2 приводится скрипт для решения данной задачи.
Данный скрипт находит самый «выгодный» путь от вершины 1 до вершины 4.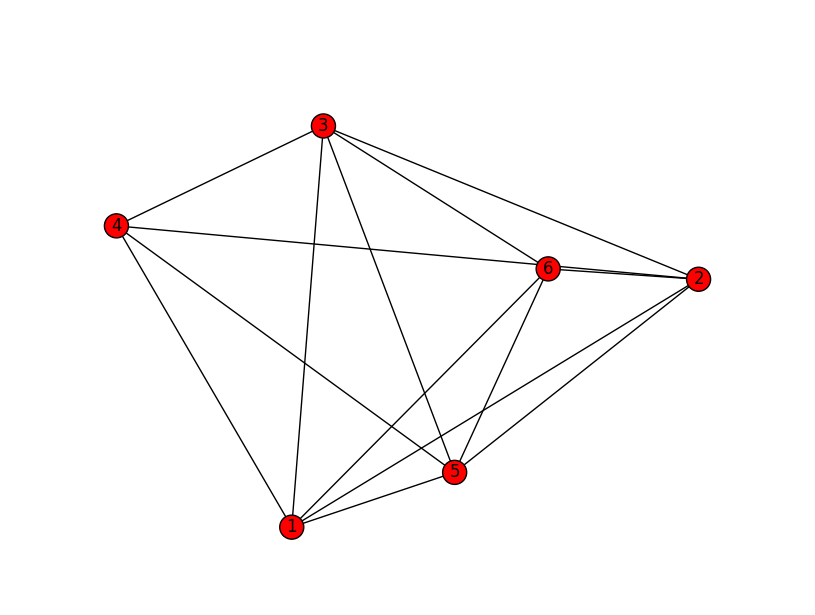 
Рис. 3.2
Листинг 2.
import networkx as nx
import matplotlib.pyplot as plt
import numpy
G = nx.Graph();
for i in range(1,6):
G.add_node(i)
G.add_edge(1, 2, node_color = 'm', weight = 2) # Параметр weight задает вес ребра
G.add_edge(1, 3, node_color = 'm', weight = 1)
G.add_edge(1, 4, node_color = 'm', weight = 20)
G.add_edge(1, 5, node_color = 'm', weight = 10)
G.add_edge(1, 6, node_color = 'm', weight = 15)
G.add_edge(5, 4, node_color = 'm', weight = 1)
G.add_edge(1, 6, node_color = 'm', weight = 10)
G.add_edge(6, 1, node_color = 'm', weight = 4)
G.add_edge(2, 3, node_color = 'm', weight = 10)
G.add_edge(2, 5, node_color = 'm', weight = 5)
G.add_edge(2, 6, node_color = 'm', weight = 20)
G.add_edge(3, 6, node_color = 'm', weight = 6)
G.add_edge(4, 2, node_color = 'm', weight = 15)
G.add_edge(4, 3, node_color = 'm', weight = 40)
G.add_edge(5, 6, node_color = 'm', weight = 10)
G.add_edge(3, 5, node_color = 'm', weight = 3)
nx.draw(G) #Отрисовка графа
plt.show()
adjacency_matrix = nx.adjacency_matrix(G)
print('Матрица стоимости')
print(adjacency_matrix) #Вывод матрицы весов
print(nx.shortest_path(G, 1, 4)) #Вывод самого короткого пути
print(nx.dijkstra_path(G, 1, 4)) #Вывод самого "выгодного" пути
Выходные данные:
[1,4] – Кратчайший путь
[1,3,5,4] – Выгодный путь
Задача о назначениях.
Задача о назначениях – одна из фундаментальных задач комбинаторной оптимизации в области математической оптимизации или исследовании операций. Задача состоит в поиске минимальной суммы дуг во взвешенном двудольном графе.
В наиболее общей форме задача формулируется следующим образом:
Имеется некоторое число работ и некоторое число исполнителей. Любой исполнитель может быть назначен на выполнение любой (но только одной) работы, но с неодинаковыми затратами. Нужно распределить работы так, чтобы выполнить работы с минимальными затратами.
Если число работ и исполнителей совпадает, то задача называется линейной задачей о назначениях. Обычно, если говорят о задаче о назначениях без дополнительных условий, имеют ввиду линейную задачу о назначениях.
Предположим, что таксомоторная компания имеет три свободные машины (исполнители), и три заказчика (работы), желающих получить такси как можно быстрее. Фирма заботится о времени доставки такси к заказчику, так что для каждой машины "стоимость" определяется скоростью, с какой машина доберётся до места ожидания, определённого заказчиком. Решением задачи о назначениях будет распределение машин по заказчикам, такое, что суммарная цена (суммарное время ожидания) минимально.
Задачу о назначениях можно сделать более гибкой. В вышеприведенном примере могут оказаться не три, а четыре свободных такси, но заказчика, по-прежнему, три. Можно назначить четвертую задачу, которую можно назвать "сиди тихо, ничего не делай", с ценой 0 для машины, которой она назначается. Задача может быть решена обычным методом и снова даст наилучшее решение.
Аналогичный приём можно использовать в случае, когда число заказов может превышать число доступных машин, и машина может быть назначена на выполнение нескольких работ, а также когда работа может быть назначена нескольким исполнителям (например, если заказчик – группа, не помещающаяся в одно такси). Можно также поставить задачу увеличения дохода, а не минимизацию цены.
Венгерский алгоритм.
Венгерский алгоритм — алгоритм оптимизации, решающий задачу о назначениях за полиномиальное время. Он был разработан и опубликован Харолдом Куном (англ.) в 1955 году. Автор дал ему имя «венгерский метод» в связи с тем, что алгоритм в значительной степени основан на более ранних работах двух венгерских математиков (Кёнига и Эгервари (англ.)).
Джеймс Манкрес (англ.) в 1957 году заметил, что алгоритм является (строго) полиномиальным. С этого времени алгоритм известен также как алгоритм Куна — Манкреса или алгоритм Манкреса решения задачи о назначениях. Временная сложность оригинального алгоритма была O(n4), однако Эдмондс (англ.) и Карп (а также Томидзава независимо от них) показали, что его можно модифицировать так, чтобы достичь времени выполнения O(n3). Форд и Фалкерсон (англ.) распространили метод на общие транспортные задачи. В 2006 году было обнаружено, что Якоби нашёл решение задачи о назначениях в XIX веке и опубликовал его в 1890 году на латыни.
Постановка задачи.
Дана неотрицательная матрица размера n×n, где элемент в i-й строке и j-ом столбце соответствует стоимости выполнения j-ого вида работ i-м работником. Нужно найти такое соответствие работ работникам, чтобы расходы на оплату труда были наименьшими. Если цель состоит в нахождении назначения с наибольшей стоимостью, то решение сводится к решению только что сформулированной задачи путём замены каждой стоимости C на разность между максимальной стоимостью и C.