Математические исследования Ньютона. Спор с Лейбницем

Математические дарования, подобно музыкальным, нередко врожденны, проявляются рано и органически определяют склад ума данного человека. Ньютон был таким врожденным математиком. «Для того чтобы научиться математике,— говорил Фонтенелль в похвальном слове памяти Ньютона в 1727 г.,— Ньютон не изучал Эвклида, который казался ему слишком ясным, слишком простым, не стоящим затраты времени; он знал его в некотором смысле раньше, чем его прочитал; один взгляд на текст теорем мгновенно создавал и доказательство. Он перешел сразу к таким книгам, как «Геометрия» Декарта и «Оптика» Кеплера. По отношению к Ньютону можно бы применить то, что Лукиан сказал о Ниле, истоки которого были неизвестны древним: «Человеку не позволено видеть Нил слабым и рождающимся». В этой пышной фразе XVIII в. есть, конечно, преувеличение и даже ошибки. Именно Эвклид, классический геометрический метод древних, был основным орудием математических изысканий Ньютона; Ньютон мыслил геометрически, а на полях экземпляра геометрии Декарта сохранилась собственноручная пометка Ньютона: «Это не геометрия». Недавно найден ньютоновский Эвклид, поля которого испещрены заметками и чертежами Ньютона (рис. 27).

Направление математической мысли Ньютона дано несомненно Барроу, его учителем; он был его непосредственным предшественником в методе флюксий. «Лекции по геометрии» И. Барроу, в редактировании которых Ньютон принимал участие, так же как и «Лекции по оптике», во многом напоминают великого ученика И. Барроу. Замечательно, что геометрические кривые для Барроу в сущности кинематические, так как изменения, выражаемые ими, трактуются как функция времени. Вводная первая лекция Барроу посвящена понятию времени. «Время, по Барроу, есть постоянство вещи в ее существовании» и является «абсолютным количеством». На вопрос о том, существовало ли время прежде вещей и можно ли говорить о времени там, где нет ничего, Барроу отвечает утвердительно, так же как и в отношении пространства. «Время,— пишет он,— не есть актуальное существование, но возможность постоянного длящегося существования, так же как пространство обозначает способность существования величины». Мы узнаем в этих словах первые эскизы ньютоновских определений пространства и времени в «Началах».

Недавно Мор опубликовал неизвестное письмо Ньютона, очень важное для понимания источников математических направлений мысли Ньютона: «Намек на метод (метод флюксий) я получил из способа Ферма проведения касательных; применяя его к абстрактным уравнениям прямо и обратно, я сделал его общим. М-р Грегори и д-р, Барроу применяли и улучшили этот метод проведения касательных. Одна моя статья послужила оказией для д-ра Барроу показать мне его метод касательных до включения его в 10-ю лекцию по геометрии. Ибо я — тот друг, о котором он там упоминает». Из письма явствует, таким образом, с несомненностью влияние работ Ферма как на Барроу, так и на Ньютона. Большое значение для обоих имели также работы Джона Уоллиса, собранные в книге «Универсальная арифметика, или новый метод исследования квадратуры кривых линий» (1665).

Все основные математические работы Ньютона фактически выполнены до того поворотного периода в девяностых годах, о котором говорилось в предыдущей главе, но в печати появились только после переселения Ньютона в Лондон. При этом опубликование математических работ у Ньютона почти во всех случаях было вынужденным главным образом спорами о приоритете с Лейбницем. Это обстоятельство весьма знаменательно. Становится ясным, что математическая работа для Ньютона имела главным образом вспомогательное значение орудия при физических изысканиях.

Выше упоминалось, что в эпоху создания «Начал» Ньютон охотно называл себя «математиком». Но при этом, надо думать, имелась цель главным образом отграничить физику принципов от физики гипотез. Физика принципов с формальной стороны подобна геометрии и построена чисто математически; физика гипотез, по крайней мере во времена Ньютона (Декарт, Гук), была совершенно далека от математической стройности, и только Гюйгенс в своем «Трактате о свете» сделал первый опыт математической обработки гипотезы (волновая гипотеза). Математика в руках Ньютона была могучим средством синтетического исследования природы. Характерно, что даже самая терминология нового исчисления бесконечно малых, введенная Ньютоном: «флюксия», «флюента» (от слова текущий), «момент», взята из механических образов и в этом смысле значительно конкретнее «дпфференциалов» и «интегралов» Лейбница. Характерно также, что в своей «Универсальной арифметике» (Arithmetica Universalis), поясняя текст, Ньютон дает иногда чисто физические задачи. Одна из них вошла во все задачники по физике, хотя происхождение ее и мало кому известно: «Камень падает в колодец; определить глубину колодца по звуку, происходящему при ударе камня о дно».

Служебная практическая роль математики в руках Ньютона не умаляет, конечно, значения его великих открытий в этой области. Новые запросы физики требовали и новой математики, новых методов. Анализ бесконечно малых был совершенно необходим для разрешения задач новой механики. Физика и математика всегда помогали одна другой, и развитие их часто не разделимо. При этом иногда физика опережала математику, ставя перед ней новые задачи, иногда, наоборот, в математике создавались целые большие разделы и главы «в прок». Физика пользовалась ими, в некоторых случаях много позднее их создания. Так, в XIX в. параллельно теории электромагнитного поля развиваются векторный анализ и теория кватернионов; в наше время, в связи с теорией относительности, стимулы к дальнейшему развитию получили тензорное исчисление и неэвклидова геометрия. Ряд задач оптики, теории газов и т. д. настойчиво требует развития теории интегральных уравнений. Для интерпретации квантовых явлений применена математическая теория групп и т. д. В наше время труд дифференцировался. Физики ставят задачи, математики дают методы их решения. Ньютон одновременно делал и то и другое.

Открытие исчисления бесконечно малых является бесспорно важнейшим фактом в истории математики и человеческой мысли вообще. Классический метод Эвклида, Архимеда, Аполлония и других геометров древности дает возможность устанавливать количественные соотношения между различными переменными величинами в некоторых даже весьма сложных случаях. Однако приемы решения почти в каждой задаче различные; нужно было обладать особым геометрическим гением Архимеда, Ньютона, Пуансо с их неисчерпаемой изобретательностью, чтобы проводить геометрический метод систематически. Великое дело Декарта — создание аналитической геометрии — перекинуло мост между алгеброй и геометрией; одно и то же соотношение при помощи метода координат стало возможным изображать аналитически (в виде формулы) или геометрически. Для решения геометрических задач открылся новый путь и обратно: геометрические задачи можно было свести к аналитическим. Оставалось, однако, одно затруднение.

Кривая фигура отличается от фигуры, ограниченной прямыми линиями, тем, что направление ограничивающей линии меняется постоянно и непрерывно: бесконечно малое продвижение по кривой сопровождается и бесконечно малым изменением направления. По таким непрерывным кривым происходят многие изменения в природе: планеты описывают эллипсы, вращающиеся тела — круги, падающие тела — параболы и т. д.; тяжелая нить, подвешенная за два конца, свешивается по так называемой цепной линии. Если изображать графически при помощи системы координат связь между явлениями природы, мы будем также получать кривые, непрерывно изменяющиеся линии. "Изображая, например, связь между объемом и давлением газа по закону Бойля-Мариотта, получим гиперболу; оптические диффракционные явления изображаются спиралью (спираль Корню) и т. д. Прямолинейная зависимость — редкий случай в природе, и потому изучение свойств кривых линий стало насущной задачей науки с давних пор. Но применение математических приемов древности к кривым линиям всегда было затруднительно. Архимед побеждал это затруднение в некоторых случаях. Первые достаточно общие приемы проведения касательных, определяющих направление кривой в каждой точке, были предложены в первой половине и в середине XVII в. Декартом, Ферма, Паскалем, Уоллисом, Барроу и др. В этих приемах было, однако, не мало дефектов. Они не только не распространялись на трансцендентные кривые, но и по отношению к алгебраическим кривым были применимы не во всех случаях. Основным недостатком была также чисто геометрическая трактовка вопроса. Нужно было найти аналитический способ, заменяющий геометрический образ касательной. Эта задача аналитической характеристики бесконечно малых изменений кривых (или, общее, функций) и была разрешена Ньютоном, повидимому, еще в шестидесятых годах XVII в. и позднее — вероятно, совершенно независимо — Лейбницем. Чертеж, изображающий некоторую кривую, отнесенную к определенным осям координат, одновременно наглядно показывает площадь, замыкаемую данной кривой, или ее отрезком. В связи с этим находится вторая основная задача анализа — выражение этих площадей, если дано уравнение кривой (квадратуры, или интегральное исчисление).

В 1669 г. Ньютон передал на просмотр Барроу мемуар «De analysi per aequationes numero terminorum infinitas» (Об анализе уравнениями бесконечных рядов); главный его предмет — квадратуры. Ньютон вычисляет площадь, описываемую кривой, выражающейся уравнением

,

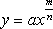и находит для площади выражение

,

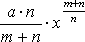Квадратура сложных кривых сводится Ньютоном к квадратуре слагаемых; указываются приемы предварительной обработки уравнении сложных кривых путем разложения дробей и корней в степенные ряды и т. д. Посылая для ознакомления рукопись Ньютона Коллинсу, Барроу рекомендует Ньютона как очень молодого еще магистра с необычайными способностями. Это сочинение, с согласия Ньютона, было издано Джонсом только в 1711 г., в связи с полемикой Ньютона и Лейбница; следов метода флюксий в нем еще нет. Последний был высказан Ньютоном и другом сочинении, изданном только после его смерти Джоном Кользоном в 1736 г. под заглавием «Метод флюксий и бесконечные ряды» (The method of fluxions and infinite series); в собраниях трудов Ньютона то же сочинение печатается под заглавием «Аналитическая геометрия» (Geometria analytica). Ньютон называет флюентами (текущими) переменные величины, входящие в уравнения. Скорости изменения прироста флюент, т. е. отношения бесконечно малого прироста одной флюенты к соответствующему бесконечно малому приросту другой флюенты, Ньютон называет флюксиями. "Бесконечно малый прирост флюенты (в общепринятой терминологии Лейбница — дифференциал) Ньютон обозначает символом о. х, самую же флюксию через х. В указанном трактате Ньютон сначала дает теорию разложения функций в ряды и затем переходит к основной задаче флюксионного исчисления: отысканию отношений флюксий, если дано соотношение между флюентами. Дается также способ вычисления отношения флюксий; далее разбирается вторая основная задача анализа бесконечно малых: из данного отношения между флюксиями найти отношение между флюентами (задача интегрального исчисления). Попутно решается ряд важнейших задач анализа: решение простейших дифференциальных уравнений, определение минимумов и максимумов функций, нахождение касательных и подкасательных, определение кривизны и точек перегиба кривых, вычисление площадей; замыкаемых кривыми, и длин отрезков кривых.

Этот перечень мало что скажет читателю, не знакомому с начатками анализа, для тех же, кому это известно, уже из одного перечня ясно, что по крайней мере дифференциальное исчисление в основных чертах изложено в трактате Ньютона. Последний, как мы уже говорили, был опубликован только после смерти Ньютона, причем издатель пользовался несколькими незаконченными манускриптами. С этой точки зрения трактат многое теряет в глазах скрупулезного судьи в смысле юридического доказательства прав Ньютона на приоритет.

Ньютон знал цену своему великому открытию и закрепил отчасти свои права письмом к Коллинсу от 1672 г. Коллинс, как в свое время говорилось, был центром научной переписки английских математиков с иностранными. Ньютон сообщил Коллинсу о своем открытии в общей форме, не указывая самого метода, а поясняя его несколькими примерами. Это письмо служило впоследствии опорным пунктом в споре Ньютона с Лейбницем.

В связи с этим придется кратко изложить перипетии этого злополучного длительного спора. Письмо к Коллинсу было послано в декабре 1672 г. В начале 1673 г. Лейбниц в течение нескольких месяцев был в Лондоне и часто посещал секретаря Королевского Общества Ольденбурга, который до известной степени был в курсе математических работ Ньютона. Из Лондона Лейбниц направился в Париж, где вместе с Гюйгенсом усиленно занялся математикой. В 1674 г. Ольденбург сообщил Лейбницу о существовании нового общего метода Ньютона, сущность метода при этом, однако, не излагалась. В 1676 г. Лейбниц проездом был снова в Англии и лично познакомился с Коллинсом. Впоследствии, в разгаре спора, защитники прав Ньютона указывали, что при этом случае Лейбниц мог узнать содержание работ Ньютона из рукописей, хранившихся у Коллинса. В 1676 г. Ньютон пишет через Ольденбурга Лейбницу письмо, в котором передает многое новое о разложении в ряды, сообщает и знаменитый бином (без доказательства); о методе бесконечно малых, однако, в письме не говорится. Только в следующем письме к Ольденбургу от 24 октября 1676 г. Ньютон говорит о новом методе. Он приводит результаты, достигнутые этим приемом, примеры его применения, самую же сущность метода сообщает в следующей зашифрованной строчке:

6aeccdae 13eff 7i 3l 9n 4о 4qrr 4s 9t 12vx;

числовые коэффициенты, стоящие перед буквами, указывают, сколько раз данная буква повторяется в тексте зашифрованной фразы. Если знать, что фраза написана по-латински, то при хорошем знакомстве с языком ее можно расшифровать. От этого, впрочем, дело не проясняется. Фраза в расшифрованном виде была опубликована в «Началах». Текст ее следующий: «Data aequatione quotcunque fluentes quantitates involvente fluxiones invenire et vice versa» (Дано уравнение, заключающее в себе текущие количества (флюенты), найти течения (флюксии) и наоборот). Понять отсюда сущность открытия было невозможно. Детальное изложение метода скрыто более сложной шифровкой. Лейбниц парирует загадки Ньютона в письме от 21 июня 1677 г. достаточно ясным изложением основ дифференциального исчисления, отличающегося по существу от метода флюксий только символикой. На этом переписка кончилась. Длительное изучение вопроса привело историков математики к единому выводу: основы анализа бесконечно малых открыты Ньютоном и Лейбницем независимо, причем несомненно, что открытие Ньютона было сделано несколькими годами раньше.

Шифровка Ньютона в письме к Лейбницу и, наоборот, открытое, ясное изложение метода Лейбницем в его ответе ставятся некоторыми историками в упрек Ньютону. Упрек едва ли справедливый. Обычай скрывать еще не вполне обработанные результаты научной работы в виде анаграмм или шифров был распространен в старые времена и сохранился в несколько измененном виде и теперь. Прямая цель при этом — предотвращение параллелизма в научных работах и сохранение за автором его прав на первенство. После того как Ньютон вполне ясно изложил ту область, на которую простирался его метод и главные результаты приложения метода, Лейбницу, конечно, ничего другого не оставалось, как показать совершенно отчетливо Ньютону, что и он, независимо, пришел к тому же методу, причем, несмотря на шифр Ньютона, нужно было изложить и самый метод. Ньютон и Лейбниц высказали в переписке только то, что вынуждены были высказать, и потому противопоставление скрытности Ньютона благородству Лейбница не основательно.

В 1684 г. в лейпцигском журнале «Acta Eruditorum» (Деяния ученых) появляется первый мемуар Лейбница, посвященный дифференциальному исчислению; при этом Лейбниц сделал непонятный тактический промах, совершенно не упоминая имени Ньютона. Ошибка исправляется во втором мемуаре, где излагаются начала интегрального исчисления. Перечисляя длинный ряд имен предшественников, подготовивших почву для создания анализа бесконечно малых, Лейбниц указывает и Ньютона. «Ньютон подошел к открытию квадратур при помощи бесконечных рядов не только совершенно независимо, но он настолько дополнил метод вообще, что издание его работ, до сих пор не получившее осуществления, явилось бы несомненно поводом новых больших успехов в науке». Эта фраза давала неопределенное представление о достижениях Ньютона. Ньютон в следующем году в первом издании «Начал» отозвался о работах Лейбница совершенно объективно.

В знаменитом «Поучении» во второй книге «Начал» Ньютон пишет следующее по поводу метода флюксий: «В письмах, которыми около десяти лет тому назад я обменивался с весьма искусным математиком Г. Г. Лейбницем, я ему сообщал, что обладаю методом для определения максимумов и минимумов, проведения касательных и решения тому подобных вопросов, одинаково приложимых как для членов рациональных, так и для иррациональных, причем я метод скрыл, переставив буквы следующего предложения: «когда задано уравнение, содержащее любое число текущих количеств, найти флюксии и обратно». Знаменитейший муж отвечал мне, что он также напал на такой метод и сообщил мне свой метод, который оказался едва отличающимся от моего, и то только терминами и начертанием формул».

Естественно поставить вопрос, весьма существенный для понимания характера Ньютона: почему же он не опубликовал своевременно своего метода? Вопрос остается и в наше время большой психологической загадкой. Есть основания полагать, как мы уже говорили, что математика в глазах Ньютона играла вспомогательную роль в физическом исследовании. Окончательную обработку мемуара о методе флюксий в 1671 г. (или около этого времени) задержали начавшиеся обширные экспериментальные исследования в области оптики; Ньютон отложил новый метод как менее важное в сравнении; с открывшейся перед ним новой областью опыта, ему некогда было окончить математическую работу. Ко времени окончания основных исследований в области света (1675-1676) началась упомянутая выше переписка Лейбница с Ньютоном, из которой последний убедился, что его метод найден другим. Ньютон закрепил свои права в указанном письме к Лейбницу, и опубликование нового метода потеряло свою остроту — метод стал уже известным, и нужно было только гарантировать приоритет. Ограничившись этим, Ньютон приступил к реализации новых огромных физических замыслов в области механики. Почему Ньютон не обработал «Начал» с математической стороны по новому методу? Об этом уже говорилось при разборе «Начал». Написать «Начала» на новом математическом языке значило сделать их непонятными никому из современников, значило вовлечься в новые неизбежные пререкания чисто математического свойства. Даже такой математик, как Гюйгенс, уже в 1692 г. писал Лейбницу, что ему непонятны преимущества дифференциального исчисления в сравнении со старыми приемами. Математическая сторона в «Началах» для Ньютона имела второстепенное значение в сравнении с их физическим содержанием. Ньютон снова пошел по линии наименьшего сопротивления, ограничившись кратким указанием наличия метода флюксий и решения нескольких задач. После издания «Начал» на очереди снова стояла важная физическая задача: детальное изучение движения Луны. Снова не было времени, и слова физика и астрономия стояли на первом месте в сравнении с математикой. Таково одно из возможных объяснений того обстоятельства, что Ньютон не печатал своего «Метода флюксий» до девяностых годов XVII в. Гигантская работа, не оставлявшая времени для издания своих трудов, кончилась, как мы знаем, умственным переутомлением и психической болезнью, после которой и характер и размеры деятельности Ньютона резко изменились. Административный пост, связанный с работой, далекой от науки, шумная жизнь Лондона, активная деятельность в Королевском Обществе — все это, конечно, отрывало от продолжения регулярных исследований.

Математический гений еще сохранился, старый лев изредка показывал когти. В 1697 г. Иоганн Бернулли сделал геометрам вызов: решить задачу о кривой, по которой тело под действием одной силы тяжести переходит из одной точки в другую. Ньютон решил задачу в несколько часов. Читая неподписанное решение в «Philosophical Transactions», Бернулли тотчас отгадал автора «tamquam ex ungue leonem» (как льва по когтям).

В девяностых годах новый анализ в форме Лейбница начал быстро прививаться. Сначала Якоб Бернулли, затем его брат Иоганн достигли поразительных успехов в новом исчислении. Во Франции маркиз Л'Опиталь издал в 1693 г. первый подробный курс дифференциального исчисления. Новый метод был принят математиками Европы и естественно связывался только с именем Лейбница, давшим анализу удобные, изящные формы и приемы. Как бы предчувствуя неизбежную борьбу за приоритет, Лейбниц в 1693 г. обратился к Ньютону с предложением возобновить переписку. Ответ Ньютона дружественный и спокойный. «Наш Уоллис,— пишет Ньютон,— присоединил к своей «Алгебре» только что появившиеся некоторые из писем, которые я писал к тебе35 в свое время. При этом он потребовал от меня, чтобы я изложил открыто тот метод, который я в то время скрыл от тебя переставлением букв; я сделал это коротко, насколько мог. Надеюсь, что я при этом не написал ничего, что было бы тебе неприятно, если же это случилось, то прошу сообщить, потому что друзья мне дороже математических открытий». Переписка на этом, однако, пресеклась.

Следует подчеркнуть необычайное спокойствие и беззаботность Ньютона по поводу своих прав в это время. Триумфальное шествие нового исчисления под маркою дифференциального исчисления Лейбница начинает, однако, беспокоить национальную гордость английских патриотов. В 1695 г. престарелый Уоллис пишет характерное письмо Ньютону: «Вы не заботитесь как следует о Вашей чести и чести нации, удерживая столь долго Ваши ценные открытия». Однако даже такие вызовы не действовали на Ньютона: он попрежнему молчал. Непосредственным зачинщиком распри Ньютона с Лейбницем явился женевский математик, переселившийся в Лондон, Фацио Дюилье (Fatio de Duillier). Обиженный на Лейбница по различным причинам, Фацио напечатал в 1699 г. небольшую книгу, в которой, между прочим, не только подчеркнул, что Ньютон первый открыл новый метод, но сделал легкий намек на возможность плагиата со стороны Лейбница. Лейбниц отнесся к этому обвинению спокойно и указал, что не имеет никакого намерения вступать с Ньютоном в прения о первенстве: он исполнен к нему глубокого уважения и уверен, что Ньютон не одобряет писаний Фацио.

Распря разгорелась снова в связи с появлением в 1704 г. «Оптики» Ньютона. К первому изданию «Оптики» Ньютон приложил два трактата: «De quadratura curvarum» (О квадратуре кривых) и «Enumeratio. linearum tertii ordinis» (Перечисление линий третьего порядка). С «Оптикой» эти мемуары соединены чисто внешним образом и в последующих изданиях опущены; появление их, несомненно, связано с начавшимися спорами, как на это и указано в предисловии. В первом трактате Ньютон дает, наконец, долгожданное печатное изложение метода флюксий и применяет его к квадратурам. Оба мемуара в своей основной части относятся, несомненно, к семидесятым годам. В безымянной, но написанной, очевидно, Лейбницем рецензии на «Оптику» в «Acta eruditorum» при всех похвалах, расточаемых по адресу Ньютона, рецензент истолковывает выводы Ньютона в терминах дифференциального исчисления Лейбница. Сам Ньютон, как он утверждал позднее, понял эту рецензию как прямое обвинение в плагиате. Распря началась; один из самых ревностных учеников Ньютона Джон Кейль обернул аргументацию рецензента и в своем мемуаре «О законе центральных сил» в 1708 г. поместил такой абзац: «Все это следует из столь знаменитого теперь метода флюксий, первым изобретателем которого был, без сомнения, сэр Исаак Ньютон, как в этом легко убедится каждый, кто прочтет его письма, опубликованные Уоллисом. То же исчисление опубликовано позднее Лейбницем в «Acta eruditorum», причем он только изменил название, вид и способ обозначений». Лейбниц, как член Королевского Общества, обратился с жалобой на Кейля к секретарю Общества. Однако обвинения Лейбница в плагиате стали раздаваться еще определеннее. Общество избрало специальную комиссию для разбора спора Лейбница с Кейлем. (Большинство комиссии состояло из приверженцев и учеников Ньютона. В середине 1713 г. вышла книга, являющаяся результатом работы комиссии, под заглавием «Commercium epistolicum D. Johanius Collins et aliorum de Analysi promota» (Переписка Д. Н. Коллинса и других о новом анализе). В книге изложена уже известная нам переписка и приведено мотивированное решение комиссии, кончающееся следующей фразой: «По этим основаниям мы считаем Ньютона первым изобретателем и думаем, что Кейль, утверждая это, не сделал ничего несправедливого по отношению к Лейбницу». «Переписка» вторым изданием появилась в 1722 г., а также вышла во Франции.

Мы не предполагаем излагать сложных перипетий этого бесполезного спора, отравлявшего последние годы жизни и Ньютону и Лейбницу. Лейбниц отвечал на «Переписку» безымянным листком, где Ньютону бросался ряд упреков; напоминалась полемика Ньютона с Гуком, присваивание Ньютоном астрономических наблюдений Флэмстида и пр. В спор вовлекались все ученики Ньютона — Кейль, Котс, Тэйлор и др. До 1714 г. сам Ньютон старался оставаться в тени, но позднее ему пришлось вести полемику и от своего имени. Спором как спортивным развлечением заинтересовался двор, разыскивались различные посредники-примирители, еще более разжигавшие страсти. Спор не кончился и со смертью Лейбница в 1716 г., принимая характер научного состязания на новом математическом поприще. Силы Ньютона слабели, ученикам же было далеко до учителя, и зачастую они терпели поражение. Ньютон умер непримиренным. В 1717 г. в примечаниях к «Истории флюксионного исчисления» Джозефа Рафсона он писал: «Заимствовал ли Лейбниц метод, или изобрел сам, не имеет абсолютного значения, ибо второй изобретатель не имеет прав». В третьем издании «Начал», изданных Пембертоном, Ньютон исключил и то знаменитое «Поучение», которое мы приводим выше и в котором отдавалось должное Лейбницу. «Поучение» заменено другим, в котором передается содержание письма к Коллинсу.

В наше время, наконец, страсти остыли. Английские историки вполне оценили заслуги Лейбница, и, наоборот, немецкие историки, по крайней мере до-гитлеровского периода, признали приоритет Ньютона. Спор остается бессмысленным фактом, на который были затрачены последние силы двух гениальных людей. Сами они спора не хотели и вовлеклись в него рядом случайностей.

Великое открытие Ньютона и Лейбница — анализ бесконечно малых — продолжало неуклонно развиваться, развивается и теперь. Это — основная математическая форма современного естествознания и техники, и нет возможности учесть те неисчислимые благие результаты, которые принес с собою анализ в области теории и техники. В символах дифференциальных и интегральных уравнений и так называемого вариационного исчисления нашли свое выражение самые общие принципы физики. Отвлеченная идея непрерывности естественных процессов и явлений, лежащая в основе анализа бесконечно малых, оказалась если не совершенно верной, то необычайно плодотворной. Новая физика в некоторых пунктах отказалась от идеи непрерывности, идея атомизации, скачков, прерывностей глубоко проникла в современную науку. Атомизируется масса, электрический заряд, энергия, действие; классические дифференциальные уравнения получают статистический смысл и предполагаются верными только для среднего значения большого числа отдельных элементарных процессов. Но и при этом ограничении принципы анализа бесконечно малых сохраняют свое руководящее значение.

Математические труды Ньютона не ограничиваются открытием флюксиониого исчисления. Знаменитая биноминальная теорема, метод приближенного решения уравнений, целый ряд замечательных геометрических теорем в «Началах», изящный трактат о кривых третьего порядка ставят Ньютона и помимо открытия анализа в число первых математиков его времени. Чтение его «Универсальной арифметики», составившейся из лекций в Кэмбридже и указанного «Перечисления кривых третьего порядка», доставит и теперь глубокое удовольствие всякому геометру и любителю математики36.

Нужно, однако, отметить еще раз, что все математические исследования Ньютона в основной части были выполнены до девяностых годов. После переезда в Лондон в 1695 г. настоящая творческая работа кончилась; с этого времени Ньютон с помощью учеников и сотрудников только подводил итоги своего творческого периода.