Методические указания к изучению дисциплины

МАТЕМАТИКА

(ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА)

Методические указания к изучению дисциплины

и выполнению семестровой работы для студентов

(выбор варианта по последней цифре зачетной книжки)

работа – №5 см. стр. 71 и

разобранный типовой пример на стр. 31

Выбор варианта описан в начале типового примера.

Содержание

1. Общие положения……………………………………………...4

2. Методические указания к изучению дисциплины.…………..4

3. Методические указания к выполнению заданий № 1- № 4

Комментарии к задаче № 1

§1. Случайные события. Основные понятия…………………….5

§2. Случайные события. Операции………………………………6

§3. Классическое определение вероятности……………………..6

§4. Примеры задач на классическую вероятностную схему……8

§5. О статистической и геометрической вероятностях…………9

§6. Простейшие свойства вероятностей………………………..10

§7. Условные вероятности. Независимость событий………….11

§8. Вероятность наступления хотя бы одного события……….12

§9. Формула полной вероятности………………………………14

§10. Формула Байеса……………………………………………..16

Комментарии к задаче № 2

§11. Повторные независимые испытания………………………17

§12. Другие формулы вычисления вероятностей для схемы Бернулли…………………………………………………………..19

Комментарии к задаче № 3

§13. Случайные величины дискретного типа…………………..22

§14. Функция распределения…………………………………….23

§15. Математическое ожидание случайной величины

дискретного типа…………………………………………………24

§16. Дисперсия случайной величины…………………………..26

§17. Биномиальный и пуассоновский законы распределения…26

Комментарии к задаче № 4

§18. Случайные величины непрерывного типа…………………28

§19. Нормальный закон распределения и его характеристики……………………………………………………30

§20. Другие законы распределения непрерывных случайных величин……………………………………………………………31

4. Методические указания к выполнению задания № 5……….32

5. Контрольные задания № 1- № 4.……………………………...53

6. Контрольные задания № 5.……………………………………71

7. Выбор варианта. Требования к оформлению контрольной работы.…………………………………………..79

8. Список литературы……………………………………….…...80

Приложение 1 Таблица случайных чисел…………….………...81

Приложение 2 Нормированная функция Лапласа.………….………83

Приложение 3 Значения чисел q в зависимости от объёма выборки n и надёжности 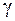для определения доверительного интервала среднего квадратического отклонения 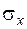.….……..85

Приложение 4 Критические точки распределения 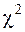...………86

Приложение 5 Содержание дисциплины..……………………..87

Приложение 6 Образец оформления титульного листа контрольной работы.…………………………………………….90

Приложение 7 Перечень контрольных вопросов для

проверки знаний по дисциплине.……………………………….91

ОБЩИЕ ПОЛОЖЕНИЯ

Цель дисциплины «Математика (Теория вероятностей и математическая статистика)» - дать необходимый математический аппарат и привить навыки его использования при решении инженерно-экономических задач. Для этого при изучении курса студенты осваивают методы математического моделирования экономических и иных возникающих на практике ситуаций, вероятностные методы их исследования и решения, методы обработки статистических данных (аналитически и при помощи вычислительной техники), а также методы дальнейшего анализа полученных результатов. Это способствует также развитию логического и алгоритмического мышления.

Теория вероятностей опирается на предшествующие разделы математики, как на курс средней школы, так и на разделы, изучавшиеся на 1 курсе (множества, функции, непрерывность, производные, интегралы, ряды).

Студенты 2 курса, имеющие зачтенные контрольные работы № 3 и № 4, допускаются к экзамену по математике.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИЗУЧЕНИЮ ДИСЦИПЛИНЫ

Изучение дисциплины следует начать с теоретической части данных методических указаний. Поскольку методические указания не являются учебником и теоретический материал здесь изложен кратко, полезно обратиться к учебникам, перечисленным в списке литературы.

Для изучения дисциплины в общепринятом логическом порядке полезно сверяться с Приложением 5 данного издания.