Задача для самостоятельного решения

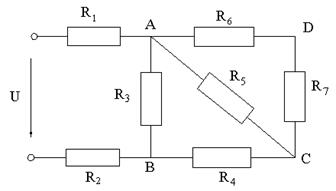
Определить токи, напряжения, мощности на отдельных участках схемы, если напряжение на входе U = 220В, а сопротивления участков схемы: R₁ = R₂ = 0,5Ом; R₃ = R₅ = 10Ом; R₄ = R₆ = R₇ = 5Ом. Составить баланс мощности.

Лабораторная работа №3

Исследование неразветвленной электрической цепи
синусоидального тока

Цель работы

Подтвердить основные теоретические соотношения для однофазной цепи синусоидального тока при последовательном соединении реальной индуктивной катушки и конденсатора экспериментом. В частности, подтвердить законы Ома и Кирхгофа для цепей синусоидального тока, резонанса напряжений и основные энергетические соотношения.

Теоретическая часть

Резонансом в электрических цепях называется режим участка электрической цепи, содержащей индуктивный и емкостный элементы, при котором угол сдвига фаз напряжения и тока участка равен нулю.

Резонанс напряжений возможен на участке цепи с последовательным соединением элементов, параметры которых r, L, и C, т.е. в последовательном контуре (см.рис. 3.2). Активное сопротивление r, показанное на схеме отдельно, может быть как сопротивлением специально включенного резистора, так и сопротивление проводов катушки индуктивности.

Действующее значение тока в последовательной цепи r, L, C определяется по закону Ома для синусоидального тока:

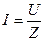, (3.1)

где: U – действующее значение напряжения, приложенного к цепи;

Z – модуль комплексного сопротивления цепи.

Если цепь содержит несколько последовательно соединенных приемников, то модуль комплексного сопротивления этой ветви равен

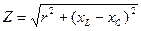, (3.2)

где: r – активное сопротивление;

x_L, x_C – соответственно индуктивное и емкостное реактивные сопротивления;

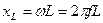; (3.3)

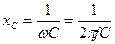, (3.4)

где L – индуктивность катушки;

С – емкость конденсатора;

ω, f – соответственно круговая частота и частота сети (в лабораторной установке f = 50 Гц).

Падения напряжения (действующее значение) на отдельных элементах последовательной цепи:

на резисторном элементе

U_r = Ir; (3.5)

на емкостном элементе

U_C = Ix_C; (3.6)

на идеальном индуктивном элементе

U_L = Ix_L (3.7)

Из соотношений (3.5) – (3.7), если известны падения напряжения на отдельных элементах, например, в результате эксперимента определяются параметры элементов:

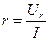; (3.8)

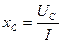; (3.9)

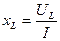. (3.10)

Падение напряжения, измеряемое на внешних зажимах реальной индуктивной катушки, равно:

U_к = IZ_к, (3.11)

откуда модуль комплексного сопротивления реальной индуктивной катушки

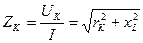. (3.12)

Активная мощность цепи

P = UIcosφ. (3.13)

Кроме того, активная мощность цепи с пассивными приемниками электрической энергии, которые выделяются только в резистивных элементах, равна:

P = I² r. (3.14)

Так как резистивный элемент при выполнении данной лабораторной работы не используется, активное сопротивление проводов обмотки реальной индуктивной катушки при известной мощности и токе в цепи определяется из соотношения (3.14) по формуле:

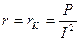. (3.15)

Реактивная мощность цепи определяется по формуле

Q = UI sinφ, (3.16)

или

Q = Q_L – Q_C, (3.17)

где: Q_L = I²x_L – реактивная мощность;

Q_C = I²x_C – реактивная емкостная мощность;

Угол сдвига фаз

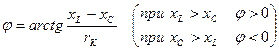. (3.18)

Полная мощность цепи

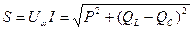. (3.19)

Ток I, напряжение U, мощность P определяются по показаниям соответствующих приборов лабораторной установки.

Для более глубокого анализа электрического состояния цепей синусоидального тока применяются векторные диаграммы. Построение векторных диаграмм начинают с выбора масштаба тока и напряжения, т.е. задаются такими значениями тока и напряжения в 1мм, которые обеспечивают хорошее заполнение рисунка векторной диаграммы. Масштабы тока и напряжения выбирают независимыми друг от друга.

При последовательном соединении элементов построение векторной диаграммы на комплексной плоскости для удобства начинают с построения в масштабе комплексного тока, полагая, что начальная фаза его равна нулю. Комплекс тока в масштабе откладывается по действительной положительной оси из начала координат. Начальная фаза приложенного напряжения к последовательной цепи для каждого опыта будет при этом различной.

Векторная диаграмма напряжений строится согласно уравнению, составленному по второму закону Кирхгофа для исследуемой последовательной цепи r, L, C

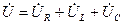. (3.20)

Комплекс напряжения 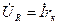(т.к. r = r_к т.е. отдельно резистивный элемент в цепи не используется) в масштабе напряжение откладывается по направлению комплекса тока, т.к. угол сдвига фаз между напряжением и током в резистивном элементе равен нулю.

А так как ток в идеальном индуктивном элементе отстает от напряжения на 90º, то комплекс напряжения 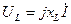в масштабе напряжения откладывается из конца вектора 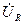под углом 90º к комплексу тока I. Ток в емкостном элементе опережает напряжение на 90º, поэтому комплекс напряжения 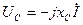в масштабе напряжения откладывается из конца вектора 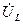под углом –90º к комплексу тока .

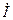В соответствии с уравнением (3.20) комплекс приложенного к цепи напряжения равен сумме комплексов напряжения 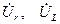и 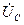. Поэтому на векторной диаграмме комплекс приложенного к цепи напряжения 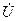определяется вектором, направленным из начала координат к концу вектора .

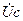При исследовании электрического состояния последовательной цепи r, L, C наиболее характерны случаи, когда x_L < x_C, x_L = x_C (резонанс напряжений) и x_L > x_C. Для указанных случаев на рис.1.1 построены векторные диаграммы тока и напряжений.