Краткие методические указания к заданиям 6 и 7

При разработке конструкторской и технологической документации различных изделий (например, сложных составных воздуховодов) часто возникает необходимость построения линий пересечения поверхностей.

Две поверхности пересекаются по линии (совокупности линий), которая одновременно принадлежит каждой из них. В зависимости от вида и взаимного положения поверхностей линия их пересечения может быть прямой (пересечение двух плоскостей); плоской (пересечение многогранника плоскостью) или пространственной (пересечение двух многогранников) ломаной; плоской (пересечение кривой поверхности плоскостью) или пространственной (пересечение двух кривых поверхностей) кривой.

Построение этой линии независимо от её формы сводится к построению ряда точек, принадлежащих одновременно каждой из пересекающихся поверхностей, и последующим их соединением в определенном порядке.

Точки, образующие линию пересечения, разделяются на опорные и промежуточные. Опорными точками являются: 1) точки, принадлежащие участвующим в пересечении ребрам многогранника; 2) очерковые точки, т.е. точки принадлежащие очеркам соответствующей проекции поверхности, которые, как правило, являются точками смены видимости линии пересечения; 3) экстремальные точки, т.е. ближайшая и самая дальняя точки линии пересечения относительно той или иной плоскости проекций. Положение опорных точек определяется в первую очередь.

Основным способом построения точек, принадлежащих линии пересечения, является способ вспомогательных поверхностей. Сущность его заключается в следующем:

Пусть заданы две пересекающиеся поверхности Ф и Ψ (рис.10).

Для построения точек линии пересечения этих поверхностей введем вспомогательную секущую поверхность S, которая пересечет поверхности Ф и Ψ по линиям m и n соответственно. Линии m и n пересекутся между собой в точках 1 и 2, поскольку они принадлежат одной поверхности S.

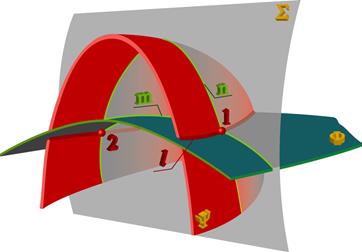Рис. 10. Взаимное пересечение поверхностей

Точки 1 и 2 будут лежать на линии l пересечения поверхностей Ф и Y, так как эти точки лежат одновременно на обеих пересекающихся поверхностях.

В качестве вспомогательных секущих поверхностей-посредников наиболее часто используют плоскости (способ вспомогательных плоскостей) или сферы (способ вспомогательных сфер). При этом всякая из проведенных поверхностей-посредников должна пересекать каждую из заданных поверхностей по линиям, проекции которых являются графически простыми линиями, например, прямыми линиями или окружностями.

Построение произвольных точек, принадлежащих линии пересечения поверхностей осуществляется по следующей схеме:

1. Вводим вспомогательную поверхность-посредник S, пересекающую заданные поверхности F и Ψ по простейшим сечениям (рис. 10).

2. Строим линии m и n пересечения поверхности S с каждой из заданных поверхностей.

3. Искомые точки 1 и 2, принадлежащие линии пересечения l заданных поверхностей, определяем в пересечении построенных линий m и n.

4. Полученные точки соединяем в требуемой последовательности с учетом видимости.

Последовательность соединения точек определяется на той плоскости проекций, где вводились вспомогательные поверхности. Видимость линии пересечения определяется простым правилом – линия является видимой на видимой поверхности.

Многократное применение указанной схемы позволяет определить необходимое количество точек (опорных и промежуточных), принадлежащих линии пересечения. Следует обратить внимание на то, что чем большее число поверхностей-посредников участвует в построениях, тем более точно выявляется характер линии (линий) пересечения поверхностей.

Задание 6

Задание 6. Построить горизонтальную проекцию шара со сквозным отверстием в виде трехгранной призмы. Радиус шара R=50мм; центр шара расположен в точке О с координатами х=90мм, y=55мм и z=50мм; фронтальная проекция отверстия задана треугольником .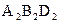

Координаты x и z точек A, B и D приведены в таблице 3. Вариант задания выбирается по последней цифре учебного шифра.

Задание может быть представлено, как задача построения линии пересечения многогранной и кривой поверхностей.

Линия пересечения многогранной и кривой поверхностей является совокупностью нескольких плоских кривых, каждая из которых - результат пересечения кривой поверхности с одной из граней многогранника (отверстия). Эти плоские кривые AB ( 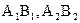), BD ( 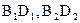) и AD ( 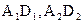) на рис. 16 попарно пересекаются в точках A ( 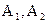), B ( 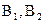) и D ( 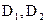) пересечения ребер многогранника (отверстия) с кривой поверхностью. В нашем случае пересечение относится к виду проницание, поэтому эта совокупность плоских кривых распадается на две части – переднюю и заднюю.

Таблица 3