Проверка гипотезы о значимости коэффициента регрессии.

Не всегда можно утверждать, что предполагаемая линейная зависимость действительно имет место.

Построив модель, описывающую изменения величин, необходимо определить верна ли она.

В регрессионном анализе проверяют гипотезы о значимости свободного члена а и о значимости коэффициента регрессии .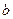

1. Определяем гипотезы H₀ и H₁:

H₀: 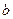=0 (между величинами нет линейной зависимости),

H₁: 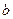≠0.

2. Зададим уровень значимости α.

3. Статистика критерия (Слайд 19).

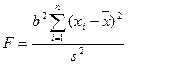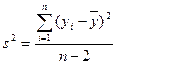, где

Статистика F имеет распределение Фишера с 1 и (n-2) степенями свободы.

4. Критические точки и критическая область.

│F│>F_α,1,n-2

5. Если 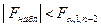, то H₀ отвергается, т.е. можно сделать вывод, что линейная зависимость значима.

Если 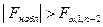, то у нас нет оснований отвергать H₀, т.е. можно сделать вывод, что линейная зависимость – незначима или что данные нельзя описать моделью линейной регрессии.

Необходимо так же просчитывать коэффициент детерминации R-квадрат, который является индикатором степени подгонки модели к данным.

Так как зависимость между величинами можно описать двумя линиями регрессии – регрессией Хна У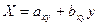

и У на Х. 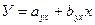, то .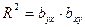

Чем меньше рассеяние наблюдаемых пар значений относительно прямых регрессии, чем больше точки примыкают к прямым, тем точнее эти прямые определены. Если значение коэффициента детерминации велико, то это означает, что точки концентрируются около прямой регрессии, а следовательно лучше будет прогноз.

Если R²=0,81, то это означает, что 81% общего рассеяния можно объяснить изменением линейной регрессии при изменении независимой случайной величины.

Задачами регрессионного анализа являются:

1. Оценить коэффициент регрессии и свободный член;
2. Определить приближенное уравнение регрессии и оценить допускаемую ошибку;
3. Проверить гипотезу о значимости регрессии.
4. Оценить степень адекватности модели.

Корреляционный анализ.

Для достаточно полного описания особенностей корреляционной зависимости между величинами недостаточно определить форму этой зависимости и в случае линейной зависимости описать ее вид по величине коэффициента регрессии. Необходимо так же оценить тесноту связи.

Корреляционный анализ экспериментальных данных для двух случайных величин заключает в себе следующие основные приемы:

1. Вычисление выборочных коэффициентов корреляции.

2. Составление корреляционной таблицы.

3. Проверка статистической гипотезы значимости связи.

Линейная корреляция

ОПРЕДЕЛЕНИЕ:Корреляционная зависимость между случайными величинами Х и 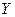называется линейной корреляцией, если обе функции регресси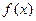и и 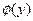являются линейными. В этом случае обе линии регрессии являются прямыми; они называются прямыми регрессии.