Тема 3. Векторная алгебра и аналитическая геометрия в пространстве

Разберите решение задачи 3 из данного пособия.

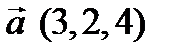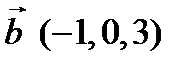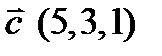Задача 3. Даны координаты векторов , и . Требуется найти:

1) длины векторов 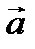, 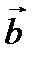и 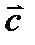; 2) скалярное произведение векторов 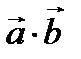и косинус угла между ними; 3) векторное произведение 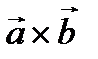и площадь треугольника, построенного на этих векторах; 4) смешанное произведение 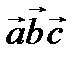и объем тетраэдра, построенного на этих векторах; 5) высоту данного тетраэдра.

Решение:

1. Длина (модуль) вектора 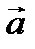вычисляется по формуле

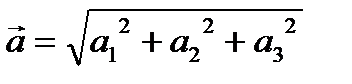(1)

Подставляя в формулу (1) координаты векторов 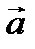, 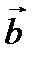и 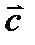, находим их модули:

; ;

.

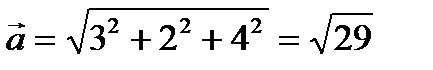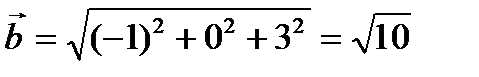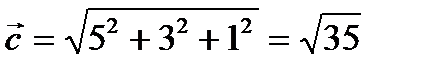2. Косинус угла 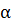, образованного векторам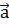и и 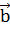равен их скалярному произведению, деленному на произведение их модулей:

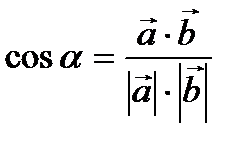(2)

Так как скалярное произведение двух векторов, заданных своими координатами, равно сумме попарных произведений одноименных координат то, 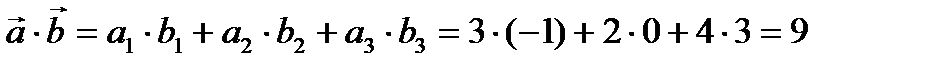. Применяя (2) имеем

.

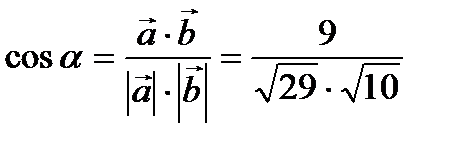3. Векторное произведение выражается формулой

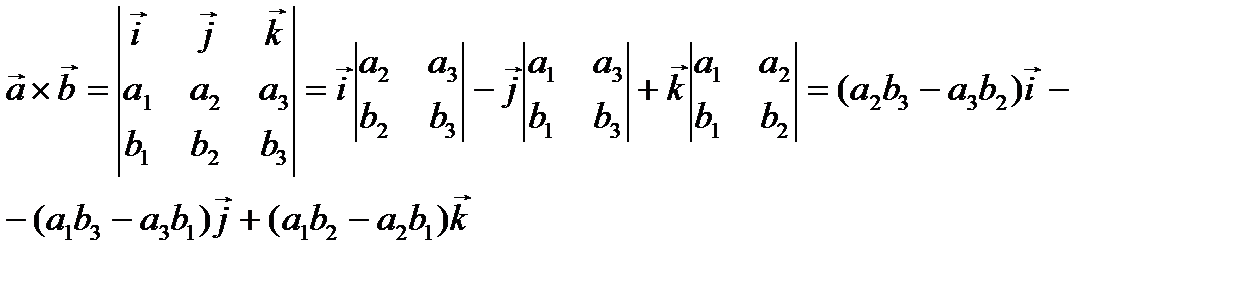
Найдем векторное произведение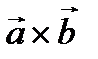

.

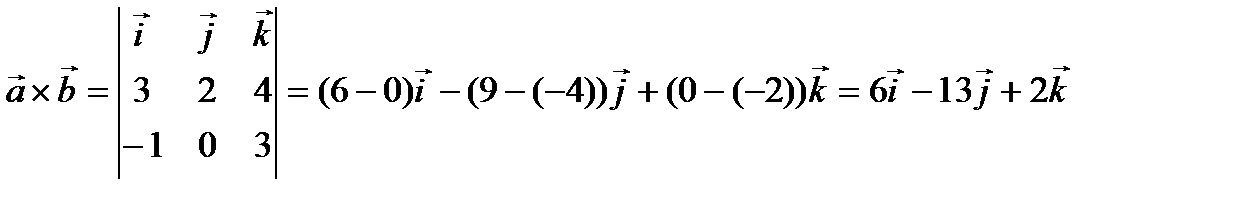Длина (модуль) векторного произведения 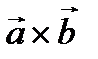численно равна площади параллелограмма, построенного на векторах 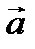и 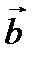. Следовательно, площадь треугольника

.

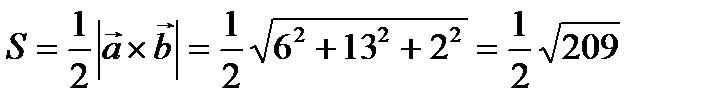4. Смешанное произведение векторов выражается формулой

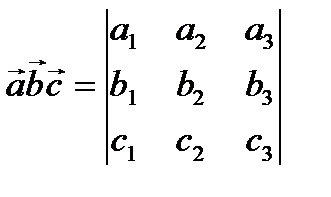
Определитель будем находить по правилу треугольников, получим

.

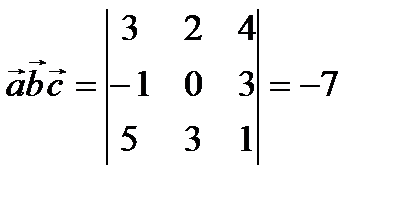Модуль смешанного произведения 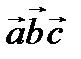равен объему V параллелепипеда, построенного на этих векторах. Объем тетраэдра 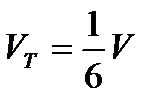, тогда .

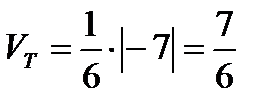5. Объем тетраэдра можно найти по формуле объема пирамиды 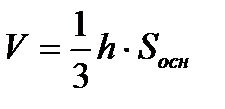, следовательно,

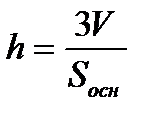(3)

Подставляя в формулу (3) полученные из пунктов 3 и 4 величины, найдем высоту тетраэдра .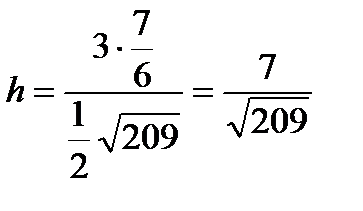

Вопросы для самопроверки

1. Какие величины называются скалярными? Векторными?

2. Какие векторы называются коллинеарными?

3. Какие два вектора называются равными?

4. Как сложить два вектора? Как их вычесть?

5. Как найти координаты вектора по координатам точек его начала и конца?

6. Назовите правила сложения, вычитания векторов, заданных в координатной форме. Как умножить вектор на скаляр?

7. Дайте определение скалярного произведения двух векторов. Перечислите основные свойства скалярного произведения.

8. Как найти скалярное произведение двух векторов по их координатам?

9. Напишите формулу для определения угла между двумя векторами.

10. Напишите условия: коллинеарности двух векторов; их перпендикулярности.

11. Напишите общее уравнение плоскости.

12. Напишите уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.

13. Какой вид имеет уравнение плоскости, проходящей через три данных точки?

14. Напишите формулу для определения расстояния от точки до плоскости.