Бигармоническое уравнение
БИГАРМОНИЧЕСКОЕ УРАВНЕНИЕ (от лат. bi-, в сложных словах - двойной, двоякий и греч. harmonikos - слаженный, соразмерный, гармоничный) - дифференц. ур-ние 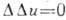 , где
, где 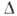 - Лапласа оператор. Решения Б. у. наз. бигармонич. функциями, к к-рым относятся, напр., гармонические функции. В приложениях чаще встречается двумерное Б. у.:
- Лапласа оператор. Решения Б. у. наз. бигармонич. функциями, к к-рым относятся, напр., гармонические функции. В приложениях чаще встречается двумерное Б. у.:
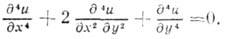
Осн. краевая задача состоит в отыскании ф-ции и(х, у), непрерывной вместе с первыми производными в замкнутой области S, удовлетворяющей Б. v. внутри S, а на её границе С -условиям: 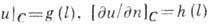 , где
, где 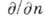 - производная но нормали к С, a g(l)и h(l) - непрерывные ф-ции дуги l. Бигармонич. ф-цию можно представить при помощи двух аналитич. ф-ций
- производная но нормали к С, a g(l)и h(l) - непрерывные ф-ции дуги l. Бигармонич. ф-цию можно представить при помощи двух аналитич. ф-ций 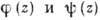 комплексного переменного z=x+iy :
комплексного переменного z=x+iy : 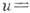
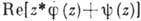 ,
, 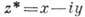 . Представление и в данном случае позволяет свести осн. краевую задачу к системе краевых задач для аналитич. ф-ций. Этот метод используют в разл. плоских задачах теории упругости и гидродинамики.
. Представление и в данном случае позволяет свести осн. краевую задачу к системе краевых задач для аналитич. ф-ций. Этот метод используют в разл. плоских задачах теории упругости и гидродинамики.
Бигармоническая функция — функция 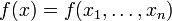 действительных переменных, определённая в области D евклидового пространства
действительных переменных, определённая в области D евклидового пространства 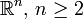 , имеющая непрерывные частные производные 4-го порядка включительно, и удовлетворяющая в D уравнению:
, имеющая непрерывные частные производные 4-го порядка включительно, и удовлетворяющая в D уравнению:
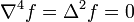
где  — оператор набла,
— оператор набла, 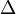 — оператор Лапласа.
— оператор Лапласа.
Данное уравнение называется бигармоническим уравнением. В декартовой системе координат в случае трёх переменных уравнение имеет вид:
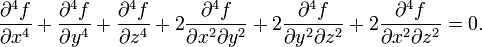
В полярных координатах:
Класс бигармонических функций включает класс гармонических функций и является подклассом класса полигармонических функций. Каждая бигармоническая функция является аналитической функцией координат xi.
Наибольшее значение с точки зрения практических применений имеют бигармонические функции 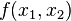 двух переменных. Такие бигармонические функции записываются с помощью гармонических функций f1, f2 или g1, g2 в виде
двух переменных. Такие бигармонические функции записываются с помощью гармонических функций f1, f2 или g1, g2 в виде
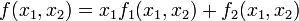
или
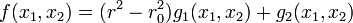
где 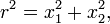 а
а 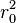 — константа.
— константа.
Основная краевая задача для бигармонических функций заключается в следующем: найти бигармоническую функцию в области D, непрерывную вместе с производными 1-го порядка в замкнутой области 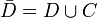 , удовлетворяющую на границе C условиям
, удовлетворяющую на границе C условиям
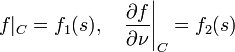
где 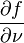 — производная по нормали до C, f1(s), f2(s) — заданные непрерывные функции длины дуги s на контуре C.
— производная по нормали до C, f1(s), f2(s) — заданные непрерывные функции длины дуги s на контуре C.
Указанные выше представления бигармонических функций позволяют получить решения краевой задачи в явному виде в случае круга D, исходя из интеграла Пуассона для гармонических функций.
Бигармонические функции двух переменных допускают также запись
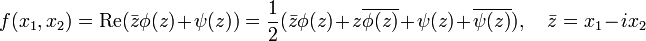
с помощью двух аналитических функций 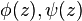 комплексной переменной
комплексной переменной 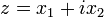 . Это представление позволяет свести краевую задачу для произвольной области D к системе краевых задач для аналитических функций, метод решения которой детально разработан Р. В. Колосовым и Н. И. Мусхелишвили. Эта методика получила развитие при решении разных плоских задач теории упругости, в которых основным бигармоническими функциями являются функция напряжений и функция Эйри.
. Это представление позволяет свести краевую задачу для произвольной области D к системе краевых задач для аналитических функций, метод решения которой детально разработан Р. В. Колосовым и Н. И. Мусхелишвили. Эта методика получила развитие при решении разных плоских задач теории упругости, в которых основным бигармоническими функциями являются функция напряжений и функция Эйри.
