Дисперсионный анализ. Регрессионный анализ (построение уравнения регрессии методом наименьших квадратов)
28.1 Дисперсионный анализ используется, когда при обработке и анализе результатов моделирования ставится задача сравнения средних значений выборок.
Допустим, изучаемый фактор Х привел к выборке значений неслучайной величины Y следующего вида: y1, y2, ¼, yk, где k – количество уровней фактора Х.
Влияние фактора Х опишем неслучайной величиной Dx, называемой факторной дисперсией
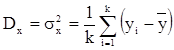 ,
,
где 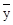 - среднее арифметическое величины Y.
- среднее арифметическое величины Y.
Пусть серия наблюдений на уровне yi имеет вид: yi1, yi1, ¼, yin, где n – число повторных наблюдений на i-м уровне. Тогда на i-м уровне среднее значение наблюдений определяется как
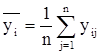 ,
,
а среднее значение наблюдений по всем уровням
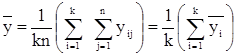 .
.
Тогда общая выборочная дисперсия всех наблюдений равна
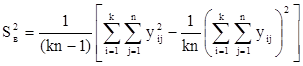 .
.
При этом, разброс значений Y определяется суммарным влиянием случайных причин и фактора Х.
Задача дисперсионного анализа состоит в том, чтобы разложить общую дисперсию D[y] на составляющие, связанные со случайными и неслучайными причинами.
Оценка генеральной дисперсии, связанной со случайными факторами
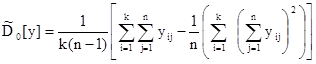 ,
,
а оценка факторной дисперсии
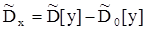 .
.
Так как факторная дисперсия наиболее заметна при анализе средних значений на
i-м уровне фактора, а остаточная дисперсия (дисперсия случайности) для средних значений в n раз меньше, чем для отдельных измерений, найдем более точную оценку выборочной дисперсии вида
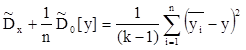 .
.
Умножив обе части этого выражения на n, получим в правой части выборочную дисперсию Sв2 , имеющую (k-1) степеней свободы. Влияние фактора Х будет значимым, если при заданном g выполняется неравенство
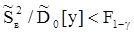 .
.
В противном случае влиянием фактора Х на результаты моделирования можно пренебречь и считать гипотезу о равенстве средних значений на различных уровнях справедливой.
Таким образом, при помощи дисперсионного анализа можно проверять гипотезу о тождественности выборочной и генеральной дисперсий.
28.2 Регрессионный анализ дает возможность построить модель, наилучшим образом соответствующую набору данных, полученных в ходе работы имитационной модели. Под наилучшим понимается минимизированная функция ошибки, являющаяся разностью между прогнозируемой моделью и данными эксперимента.
Рассмотрим случай, когда независимая переменная – одна, а уравнение линейно. Коэффициенты будем обозначать через b с разными индексами. Таким образом, для случая объекта с одним входом и выходом, результаты измерения xi и yi могут иметь вид, как это показано на рисунке 16.
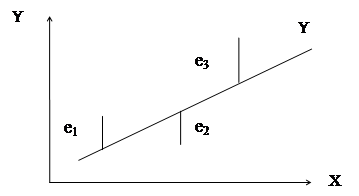 |
Рисунок 16 – Построение уравнения регрессии
Из анализа расположения точек xi и yi можно сделать вывод, что модель объекта может быть представлена уравнением прямой линии (19). Численным подтверждением этого предположения может служить величина коэффициента корреляции
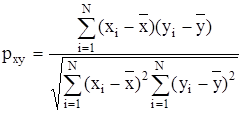 , (20)
, (20)
где 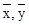 - средние значения, вычисляемые по формуле (15).
- средние значения, вычисляемые по формуле (15).
Если 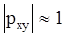 , то имеет место линейная зависимость вида (19). В противном случае, если
, то имеет место линейная зависимость вида (19). В противном случае, если 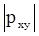 <<1, то между x и y линейная связь отсутствует. Полагая наличие линейной зависимости (19), определяют такие значения коэффициентов b0 и b1, при которых сумма квадратов ошибок является минимальной. На рисунке ошибка
<<1, то между x и y линейная связь отсутствует. Полагая наличие линейной зависимости (19), определяют такие значения коэффициентов b0 и b1, при которых сумма квадратов ошибок является минимальной. На рисунке ошибка 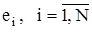 для каждой экспериментальной точки определяется как расстояние по вертикали от этой точки до линии регрессии y. Обозначим расчетные yi через
для каждой экспериментальной точки определяется как расстояние по вертикали от этой точки до линии регрессии y. Обозначим расчетные yi через 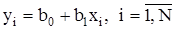 . Тогда выражение для ошибок, разность между опытными значения yi и расчетными yi, будет иметь вид
. Тогда выражение для ошибок, разность между опытными значения yi и расчетными yi, будет иметь вид
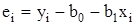 .
.
Трудность заключается в том, что наименьшим должно быть не одно такое отклонение, а сумма всех отклонений сразу
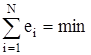 ,
,
но тогда отклонения рассматриваются не только по величине, а и по знаку. Потребуем, чтобы сумма отклонений была минимальной по абсолютной величине
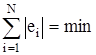 .
.
Нахождение минимума связано с дифференцированием, а продифференцировать сумму не всегда возможно. Абсолютные величины как функции имеют точку излома при значении, равном нулю; в этой точке производная имеет разрыв. Поэтому желательно найти другую функцию, которая так же, как абсолютная величина, всегда была бы неотрицательной. Простейшая из таких функций – квадрат. Если мы начнем суммировать квадраты отклонений 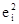 , то все члены суммы будут неотрицательны. Поэтому чаще всего задачу аппроксимации функции по опытным точкам решают на основе критерия
, то все члены суммы будут неотрицательны. Поэтому чаще всего задачу аппроксимации функции по опытным точкам решают на основе критерия
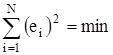 .
.
Такой вид аппроксимации называют методом наименьших квадратов. Тогда функция ошибки имеет вид
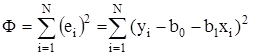 .
.
Для получения b0 и b1, при которых Ф является минимальной, принимаются необходимые условия минимума:
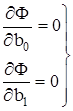 .
.
Дифференцируя (при дифференцировании следует помнить, что производная суммы равна сумме производных) Ф по b0 и b1 ,получаем:
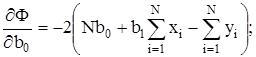 (21)
(21)
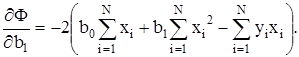 (22)
(22)
Приравняв к нулю уравнения (21) и (22) и сократив на постоянный множитель
(-2), получим нормальные уравнения
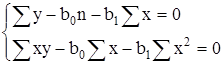 .
.
Решая эти уравнения относительно b0 и b1, получаем:
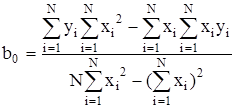 ; (23)
; (23)
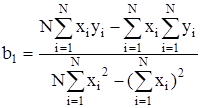 . (24)
. (24)
Мерой ошибки регрессионной модели служит среднеквадратичное отклонение
s= 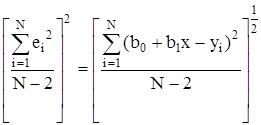 .
.
Для нормально распределенных процессов приблизительно 67% точек находится в пределах одного отклонения s от линии регрессии и 95% точек - в пределах 2s. Для проверки точности используются критерии Фишера и Стьюдента.
29 Понятие адекватности. Критерии согласия: Пирсона (c2 – критерий), Смирнова, Стьюдента (t - критерий), Фишера (F - критерий), Кохрена (У - критерий), Чеснокова, Колмогорова
Если результаты моделирования подтверждаются и могут служить основой для прогнозирования процессов, протекающих в исследуемых объектах, то говорят, что модель адекватна объекту. При этом адекватность модели зависит от цели моделирования и принятых критериев.
Задача проверки адекватности модели заключается в построении критерия для проверки нулевой гипотезы Н0.
29.1 Критерий согласия Пирсона (критерий c2). Н0 – о виде распределения.
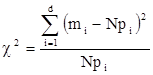 ,
,
где 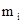 - количество значений случайной величины h, попавших в i-й подинтервал;
- количество значений случайной величины h, попавших в i-й подинтервал;
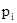 - вероятность попадания случайной величины h в i-й подинтервал, вычисленный из теоретического распределения;
- вероятность попадания случайной величины h в i-й подинтервал, вычисленный из теоретического распределения;
d - количество подинтервалов, на которые разбит интервал измерения.
Была выдвинута гипотеза H0 o том, что полученные интервалы времени на набор строк задания подчиняются нормальному закону распределения. По вычисленному U=c2, числу степеней свободы k=d-r-1 (r – число параметров теоретического закона распределения) и таблиц находят вероятность 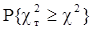 . Если эта вероятность превышает некоторый уровень значимости g, то гипотеза Н0 принимается.
. Если эта вероятность превышает некоторый уровень значимости g, то гипотеза Н0 принимается.
29.2 Критерий согласия Кокрена (Y - критерий). Н0 – однородность выборки. Используется следующая формула
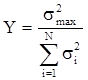 .
.
где 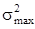 - максимальная из всех дисперсий параллельных опытов;
- максимальная из всех дисперсий параллельных опытов;
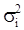 - оцениваемая дисперсия.
- оцениваемая дисперсия.
По вычисленному Y, числу степеней свободы k=N-1 и таблиц находят 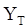 - табличные значения. Гипотеза Н0 применяется, если
- табличные значения. Гипотеза Н0 применяется, если 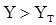 при некотором уровне значимости g.
при некотором уровне значимости g.
29.3 Критерий согласия Колмогорова. Н0 – о виде распределения.
В качестве меры распределения случайной величены используется D, вычисленная по формуле
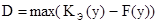 .
.
Из теоремы Колмогорова следует, что 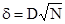 ,
, 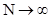 и имеет функцию распределения:
и имеет функцию распределения:
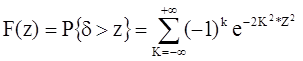 , z>0.
, z>0.
Если вычисленное на основе экспериментальных данных значение d меньше, чем табличное при выбранном уровне значимости g, то гипотезу Н0 принимают. В противном случае расхождение между FЭ(y) и F(y) считается неслучайным и Н0 отвергают.
Данный критерий целесообразно применять в тех случаях, когда известны все параметры теоретической функции распределения.
29.4 Критерий согласия Чеснокова. В ситуациях, когда приходится анализировать материалы свободного описания объектов, т.е. выбирать произвольно избирательные качественные критерии, возникает необходимость установить значимость сходства характеристик приписываемых различным объектам. Это реализуется с помощью вычисления дефекта связи D и ее объема C между двумя наборами соответствующих характеристик.
Если К0 – число элементов характеристик, вошедших в оба ряда свойств сравниваемых объектов;
К1 – число элементов, включенных в ряд описания 1-го объекта;
К2 – число элементов, включенных в ряд описания 2-го объекта;
то для вычисления дефекта связи D и объема связи С:
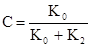 ,
, 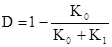 .
.
Если 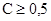 , а
, а 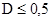 , то между двумя рядами характеристик существует значимая связь, а сходство рассматриваемых в описании объектов достоверное.
, то между двумя рядами характеристик существует значимая связь, а сходство рассматриваемых в описании объектов достоверное.
29.5 Критерий согласия Фишера (F-критерий). Н0 заключающейся в принадлежности двух выборок одной и той же генеральной совокупности.
Пусть надо сравнить две дисперсии 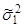 и
и 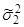 , полученные результаты при моделировании со степенями свободы k1 и k2, k1=N1-1, k2=N2-1. Причем
, полученные результаты при моделировании со степенями свободы k1 и k2, k1=N1-1, k2=N2-1. Причем 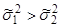 , для того, чтобы опровергнуть нулевую гипотезу Н0:
, для того, чтобы опровергнуть нулевую гипотезу Н0: 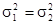 , надо при уровне значимости g указать значимость расхождения между
, надо при уровне значимости g указать значимость расхождения между 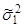 и
и 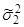 . При условии независимости выборок, взятых из нормативных совокупностей, в качестве критерия значимости используется F-критерий
. При условии независимости выборок, взятых из нормативных совокупностей, в качестве критерия значимости используется F-критерий
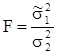 .
.
Вычисляют F, определяют k1 и k2 и при выбранном уровне значимости g по таблицам F-распределений находят значения границ критической области:
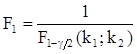 и
и 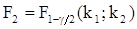 .
.
Затем проверяется неравенство: 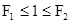 . Если неравенство выполняется, то с доверительной вероятностью b гипотеза Н0 принимается.
. Если неравенство выполняется, то с доверительной вероятностью b гипотеза Н0 принимается.
29.6 Критерий согласия Стьюдента (t-критерий). Сравнение средних значений двух независимых выборок, взятых из нормальных совокупностей с неизвестными, но равными дисперсиями D[u]=D[z], сводится к проверке нулевой гипотезы Н0: 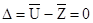 .
.
Для проверки гипотезы необходимо вычислить t:
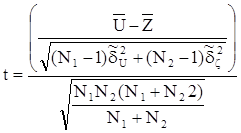 ,
,
где N1 и N2 – объем выборок для оценки 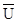 и
и 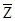 ;
;
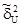 и
и 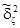 - оценки дисперсий.
- оценки дисперсий.
Затем определяется число степеней свободы k и при выбранном уровне значимости g и таблиц сравнивают t и tg. Если |t|<tg, то гипотезу Н0 принимают.
29.7 Критерий согласия Смирнова. Н0: две выборки принадлежат одной и той же генеральной совокупности. Если выборки независимы между собой и законы распределения совокупностей F(u) и F(z), из которых извлечены выборки, являются непрерывными функциями своих аргументов n и z, то для проверки нулевой гипотезы Н0 можно использовать критерий Смирнова.
По имеющимся результатам вычисляют эмпирические функции распределений Fэ(u) и Fэ(z) и определяют
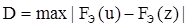 .
.
Если при выбранном уровне значимости g выполняется соотношение
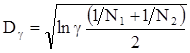 ,
,
где N1 и N2 объемы сравниваемых выборок для FЭ(u) и FЭ(z) и проводится сравнение D и Dg, если D> Dg, то нулевая гипотеза Н0 о тождественности законов распределений F(u) и F(z) с доверительной вероятностью 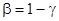 отвергается.
отвергается.
