Дифференциал функции одной переменной для приближенных вычислений

Коль скоро мы не объяснили (на данный момент) строго, что такое производная функции, то не имеет смысла объяснять, и что такое дифференциал функции. В самой примитивной формулировке дифференциал – это «почти то же самое, что и производная». Точнее – это производная, умноженная на приращение аргумента функции.

Производная функции чаще всего обозначается через .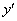

Дифференциал функции стандартно обозначается через 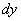(так и читается – «дэ игрек»)

Дифференциал функции одной переменной записывается в следующем виде:

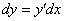
Другой вариант записи: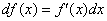

Простейшая задача: Найти дифференциал функции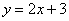

1) Первый этап. Найдем производную:

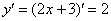
2) Второй этап. Запишем дифференциал:

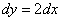
Готово.

Дифференциал функции одной или нескольких переменных чаще всего используют для приближенных вычислений.

Помимо других задач с дифференциалом время от времени встречается и «чистое» задание на нахождение дифференциала функции. Кроме того, как и для производной, для дифференциала существует понятие дифференциала в точке. И такие примеры мы тоже рассмотрим.

Пример 7

Найти дифференциал функции .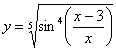

Перед тем, как находить производную или дифференциал, всегда целесообразно посмотреть, а нельзя ли как-нибудь упростить функцию (или запись функции) ещё додифференцирования? Смотрим на наш пример. Во-первых, можно преобразовать корень:

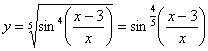(корень пятой степени относится именно к синусу).

Во-вторых, замечаем, что под синусом у нас дробь, которую, очевидно, предстоит дифференцировать. Формула дифференцирования дроби очень громоздка. Нельзя ли избавиться от дроби? В данном случае – можно, почленно разделим числитель на знаменатель:

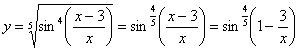
Функция сложная. В ней два вложения: под степень вложен синус, а под синус вложено выражение 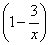. Найдем производную, используя правило дифференцирования сложной функции 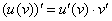два раза:

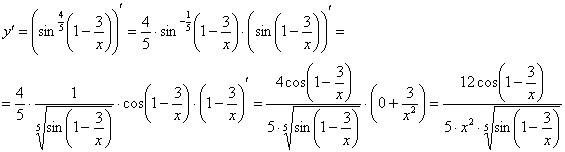
Запишем дифференциал, при этом снова представим 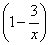в первоначальном «красивом» виде:

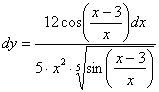
Готово.

Когда производная представляет собой дробь, значок 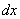обычно «прилепляют» в самом конце числителя (можно и справа на уровне дробной черты).

Пример 8

Найти дифференциал функции .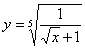

Это пример для самостоятельного решения.

Следующие два примера на нахождение дифференциала в точке.

Пример 9

Вычислить дифференциал функции 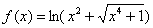в точке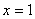

Найдем производную:

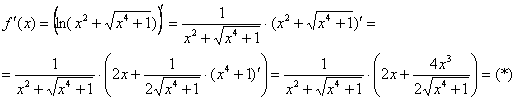
Производная вроде бы найдена. Но в это всё предстоит еще подставлять число, поэтому результат максимально упрощаем:

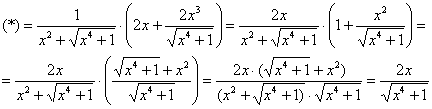
Труды были не напрасны, записываем дифференциал:

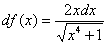
Теперь вычислим дифференциал в точке :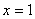

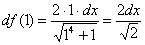
В значок дифференциала 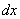единицу подставлять не нужно, он немного из другой оперы.

Ну и хорошим тоном в математике считается устранение иррациональности в знаменателе. Для этого домножим числитель и знаменатель на 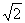. Окончательно:

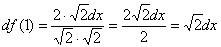
Пример 10

Вычислить дифференциал функции 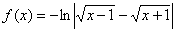в точке 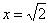. В ходе решения производную максимально упростить.

Это пример для самостоятельного решения. Примерный образец оформления и ответ в конце урока.

Вторая производная

Всё очень просто. Вторая производная – это производная от первой производной: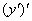

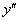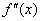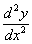Стандартные обозначения второй производной: , или (дробь читается так: «дэ два игрек по дэ икс квадрат»).

Чаще всего вторую производную обозначают первыми двумя вариантами. Но третий вариант тоже встречается, причем, его очень любят включать в условия контрольных заданий, например: «Найдите 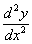функции…». А студент сидит и битый час чешет репу, что это вообще такое, и почему в дроби d не сокращены.

Рассмотрим простейший пример. Найдем вторую производную от функции .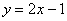

Для того чтобы найти вторую производную, как многие догадались, нужно сначала найти первую производную:

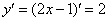
Теперь находим вторую производную:

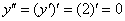
Готово.

Рассмотрим более содержательные примеры.

Пример 11

Найти вторую производную функции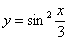

Найдем первую производную:

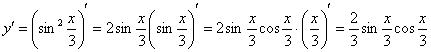
На каждом шаге всегда смотрим, нельзя ли что-нибудь упростить? Сейчас нам предстоит дифференцировать произведение двух функций, и мы избавимся от этой неприятности, применив известную тригонометрическую формулу 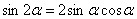. Точнее говоря, использовать формулу будем в обратном направлении: :

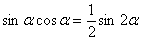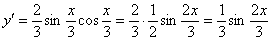
Находим вторую производную:

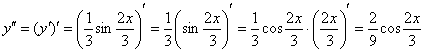
Готово.

Можно было пойти другим путём – понизить степень функции еще перед дифференцированием, используя формулу :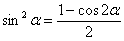

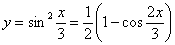
Если интересно, возьмите первую и вторую производные снова. Результаты, естественно, совпадут.

Отметим, что понижение степени бывает очень выгодно при нахождении частных производных функции. Здесь же оба способа решения будут примерно одинаковой длины и сложности.

Как и для первой производной, можно рассмотреть задачу нахождения второй производной в точке.

Например: Вычислим значение найденной второй производной в точке :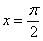

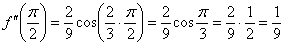
Необходимость находить вторую производную и вторую производную в точке возникает при исследовании графика функции на выпуклость/вогнутость и перегибы.

Пример 12

Найти вторую производную функции 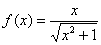. Найти .

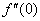Это пример для самостоятельного решения.

Аналогично можно найти третью производную, а также производные более высоких порядков. Такие задания встречаются, но значительно реже.

Решения и ответы:

Пример 2: Найдем производную:

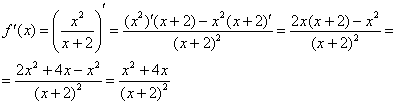
Вычислим значение функции в точке :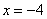

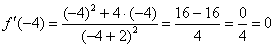
Пример 4: Найдем производную:

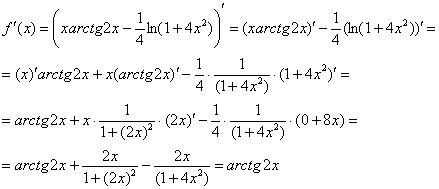
Вычислим производную в заданной точке:

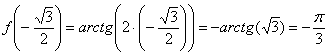
Пример 6: Уравнение касательной составим по формуле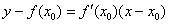

1) Вычислим значение функции в точке :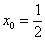

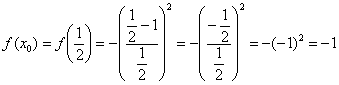
2) Найдем производную. Перед дифференцированием функцию выгодно упростить:

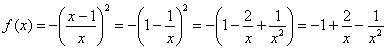
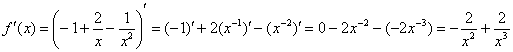
3) Вычислим значение производной в точке :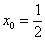

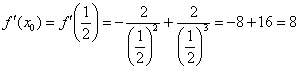
4) Подставим значения 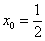, 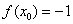и 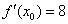в формулу :

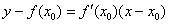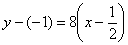
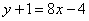
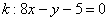
Пример 8: Преобразуем функцию:

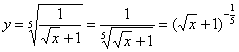
Найдем производную:

Запишем дифференциал:

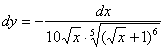
Пример 10: Найдем производную:

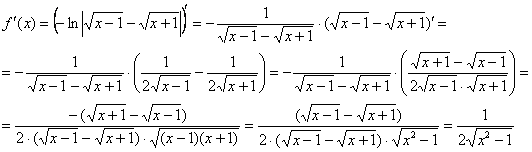
Запишем дифференциал:

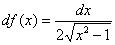
Вычислим дифференциал в точке :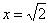

.

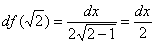Пример 12: Найдем первую производную:

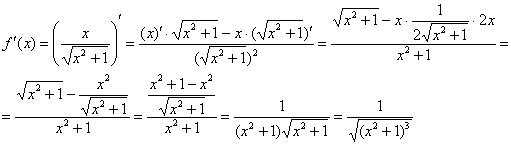
Найдем вторую производную:

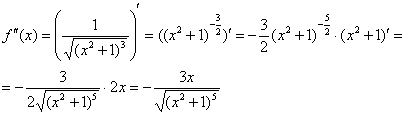
Вычислим: 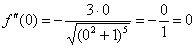.