Мультиколлинеарность факторов, экономическая сущность

Мультиколлинеар­ность - линейная взаимосвязь двух или нескольких объясняющих пе­ременных. Причем, если объясняющие переменные связаны строгой функциональной зависимостью, то говорят о совершенной мультикол­линеарности. На практике можно столкнуться с очень высокой (или близкой к ней) мультиколлинеарностью - сильной корреляционной зависимостью между объясняющими переменными.

Суть мультикол­линеарности:

Мультиколлинеарность может быть проблемой - в случае множественной регрессии. Её суть можно представить на примере со­вершенной мультиколлинеарности.

Пусть уравнение регрессии имеет вид Y= β₀+ β₁×X₁+ β₂×X₂+ε (1)

Пусть также между объясняющими переменными существует строгая линейная зависимость: X₂= γ₀+γ₁×X₁ (2) 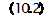Подставив (2) в (1), получим:

Y= β₀+ β₁×X₁+ β₂×( γ₀+γ₁×X₁ ) + ε или Y= (β₀+ β₂× γ₀) +(β₁+ β₂× γ₁)X₁ + ε

Обозначив β₀+ β₂× γ₀=a, β₁+ β₂× γ₁=b получаем уравнение парной линейной регрессии:

Y= a +b×X₁ + ε (3)

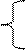Определяем коэффициенты а и b. Полу­чим систему двух уравнений (4):

β₀+ β₂× γ₀=a

β₁+ β₂× γ₁=b

В систему (4) входят три неизвестные β_0, β_1,β₂ (коэффициен­ты γ₀ и γ₁ определены в (2)). Такая система в подавляющем числе случаев имеет бесконечно много решений. Таким образом, совершенная мультиколлинеарность не позволяет однозначно определить коэффициенты регрессии уравнения (1) и разделить вклады объяс­няющих переменных X₁ и X₂ в их влиянии на зависимую переменную У. В этом случае невозможно сделать обоснованные статистические выводы об этих коэффициентах. Следовательно в случае мультиколлинеарности выводы по коэффициентам и по самому уравнению рег­рессии будут ненадежными.

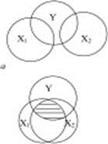Совершенная мультиколлинеарность является скорее теоретиче­ским примером. Реальна же ситуация, когда между объясняющими переменными существует довольно сильная корреляционная зависи­мость, а не строгая функциональная. Такая зависимость называется несовершенной мультиколлинеарностью. Она характеризуется высо­ким коэффициентом корреляции ρ между соответствующими объяс­няющими переменными. Причем, если значение ρ по абсолютной ве­личине близко к единице, то говорят о почти совершенной мультиколлинеарности. В любом случае мультиколлинеарность затрудняет разделение влияния объясняющих факторов на поведение зависимой переменной и делает оценки коэффициентов регрессии ненадежными Данный вывод наглядно подтверждается с помощью диафаммы Венна (рис. 1).

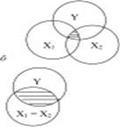
На рис. 1. а) коррелированность между объясняющими переменными X₁ и X₂ отсутствует и влияние каждой из них на Y находит отражение в наложении кругов X₁ и X₂ на круг Y. По мере усиления линейной зависимости между X₁ и X₂ соответствующие круги все больше накладываются друг на друга. Заштрихованная область отражает совпадающие части влияния X₁ и X₂ на Y. На рис. 1б при со­вершенной мультиколлинеарности невозможно разграничить степени индивидуального влияния объясняющих переменных X₁ и X₂ на зави­симую переменную Y.

Последствия мультиколлинеарности:

Обычно выделяются следующие последствия мультиколлинеарности:

1. Большие дисперсии (стандартные ошибки) оценок. Это затрудняет нахождение истинных значений определяемых величин и расширя­ет интервальные оценки, ухудшая их точность.

2. Уменьшаются t-статистики коэффициентов, что может привести к неоправданному выводу о существенности влияния соответствую­щей объясняющей переменной на зависимую переменную.

3. Оценки коэффициентов по MIIK и их стандартные ошибки стано­вятся очень чувствительными к малейшим изменениям данных, т. е. они становятся неустойчивыми.

4. Затрудняется определение вклада каждой из объясняющей пере­менных в объясняемую уравнением регрессии дисперсию зависи­мой переменной.

5. Возможно получение неверного знака у коэффициента регрессии.

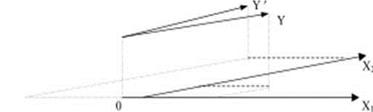
Причину последствий 3, 4 можно наглядно проиллюстрировать на примере регрессии (1) - как проекцию вектора Y на плоскость векторов X₁ и X₂. Если между этими векторами существует тесная линейная зависимость, то угол между векторами X₁ и X₂ мал. В силу этого операция проектирования становится неустойчивой: небольшое изменение в исходных данных может привести к существенному изменению оценок. На рис. 2 векторы Y и Y' различаются незначительно, но в силу малого угла между X₁ и X₂ координаты векторов Y и Y' не только значительно различаются по величине, но и по знаку.

Определение мультиколлинеариости (признаки, по которым м.б. установлено наличие):

1. Коэффициент детерминации R² достаточно высок, но некоторые из коэффициентов регрессии статистически незначимы, т.е. они имеют низкие t-статисгики.

2. Парная корреляция между малозначимыми объясняющими пере­менными достаточно высока. Данный признак будет надежным лишь в случае двух объясняющих переменных. При большем их количество более целесо­образным является использование частных коэффициентов корреля­ции.

3. Высокие частные коэффициенты корреляции.

Частные коэффициенты корреляции определяют силу линейной зависимости между двумя переменными без учета влияния на них других переменных. Однако при изучении многомерных связей в ряде случаев парные коэффициенты корреляции могут давать совершенно неверные представления о характере связи между двумя переменны­ми. Например, между двумя переменными X и Y может быть высокий положительный коэффициент корреляции не потому, что одна из них стимулирует изменение другой, а оттого, что обе эти переменные из­меняются в одном направлении под влиянием других переменных, как учтенных в модели, так и, возможно, неучтенных. Поэтому имеется необходимость измерять действительную тесноту линейной связи ме­жду двумя переменными, очищенную от влияния на рассматриваемую пару переменных других факторов. Коэффициент корреляции между двумя переменными, очищенными от влияния других переменных, на­зывается частным коэффициентом корреляции.

4) Сильная вспомогательная (дополнительная регрессия)

Мультиколлинеарность может иметь место вследствие того, что какая-либо из объясняющих переменных является линейной комбинацией других объясняющих переменных. Для данного анализа строятся уравнения регрессии каждой из объясняющих переменных X_j, где j=1,2 …,m на оставшиеся объясняющиеся переменные вспомогательные регрессии. Вычисляются соответствующие коэффициенты детерминации 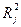и рассчитывается их статистическая значимость на основе F-статистики

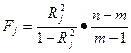n – число наблюдений, m – число объясняющих переменных в первоначальном уравнении регрессии. Статистика F имеет распределение Фишера с ν₁=m-1 и ν₁=n-m степенями свободы. Если 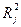статически не значим, то X_j не является линейной комбинацией других переменных и её можно оставить в уравнении регрессии. Иначе, есть основания считать, что X_j существенно зависти от других объясняющих переменных и имеет место мультиколлинеарность.