Решение линейных алгебраических систем

ЕТИ.М. 01

Егорьевск 2010

Составитель доцент, к.ф-м.н. Коняшкин А.К.

Рецензент доцент, к.ф-м.н. Бармакова Т.В.

При выполнении первой лабораторной работы студенты осваивают стандартные программные структуры и команды EXCEL,: числа, матрицы, , действия с массивами.

Методические указания предназначены для студентов 1и 2 курсов, обучающихся по специальностям: 151001 «Технология машиностроения», 220301- «Автоматизация технологических процессов и производств (машиностроения)», 080502 -- «Экономика и управление на предприятии (в машиностроении)», 330200 -- "Инженерная защита окружающей среды"

Методические указания обсуждены на заседании кафедры естественно-научных дисциплин.

Протокол № 4 от 21 января 2010 г.

Заведующий кафедрой А.П. Нилов

Методические указания рассмотрены и одобрены методическим советом института

Протокол № от

Председатель совета А.Д.Семенов

СОДЕРЖАНИЕ

1. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.. 3

2. РЕШЕНИЕ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ СИСТЕМ... 4

2.1. Табличные формулы и операции с матрицами. 5

2.2. Группировка рабочих листов. 6

2.3. Метод Крамера. 8

2.4. Матричный способ решения. 10

2.5. Поиск решения. 11

3. ЗАДАНИЕ ДЛЯ ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ... 13

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ... 16

СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Многие задачи экономического характера сводятся к решению систем линейных уравнений. Систему [1] вида

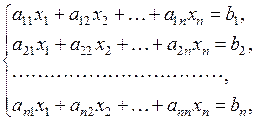(1)

принято называть системой n линейных алгебраических уравнений (СЛАУ) с n неизвестными. При этом произвольные числа a_ij (i = 1, 2,…, n; j = 1, 2,…, n) называются коэффициентами системы (коэффициентами при неизвестных), а числа b_i (i = 1, 2,…, n) – свободными членами. Такая форма записи (1) алгебраической линейной системы называется нормальной. Решением СЛАУ (1) называется совокупность чисел x_i (i = 1, 2,…, n), при подстановке которых в систему каждое из ее уравнений обращается в тождество.

Систему (1) можно записать в матричной форме

A ´ X = B,

(2)

где A – матрица коэффициентов при неизвестных (матрица системы):

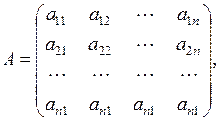(3)

X – вектор-столбец неизвестных X = (x₁, x₂, …, x_n)^T:

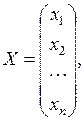(4)

B – вектор-столбец свободных членов:

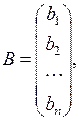(5)

или B = (b₁, b₂,..., b_n)^T. Целое число n называется размерностью системы.

Система (2) может быть записана в развернутом виде

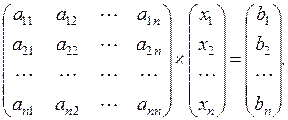(6)

Система уравнений (6) называется совместной, если она имеет хотя бы одно решение, и несовместной – в противном случае. Совместная система (6) называется определенной, если она имеет единственное решение, и неопределенной, если она имеет больше одного решения.

РЕШЕНИЕ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ СИСТЕМ

Вопросы исследования СЛАУ (6) на совместность оставим за пределами нашего рассмотрения. Все же методы решения линейных алгебраических систем принято делить на два класса: прямые и итерационные. Прямыми называются методы решения СЛАУ, которые приводят к решению за конечное число арифметических операций. В случае точной реализации операций решение будет точным, поэтому и прямые методы иногда называют точными. Итерационными методами называют такие методы, в которых точное решение может быть получено за счет реализации многократно повторяющихся действий (итераций). Эффективность способов решения системы (6) во многом определяется свойствами матрицы (3) A (размерностью, симметричностью, заполненностью и т.д.). MS Excel располагает рядом возможностей для работы с матрицами.