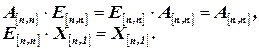Матрицы и действия над ними
Системы линейных уравнений
Понятия системы линейных уравнений и ее решения
Системы линейных уравнений – это системы уравнений первой степени с несколькими неизвестными:
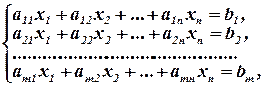
где 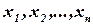 - неизвестные;
- неизвестные;
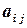 - коэффициент при неизвестном
- коэффициент при неизвестном 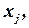
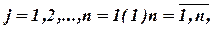 в
в 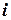 -ом уравнении,
-ом уравнении, 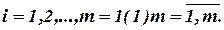
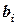 - свободный член
- свободный член 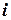 -ого уравнения.
-ого уравнения.
В компактном виде эту систему можно представить в записи:
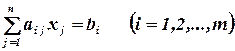 .
.
В отличие от элементарной алгебры в линейной алгебре изучаются системы линейных уравнений с произвольным числом уравнений и неизвестных.
Решением системы линейных уравнений называется такая совокупность 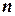 чисел
чисел 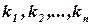 , что каждое из этих уравнений обращается в тождество после замены в нем неизвестных
, что каждое из этих уравнений обращается в тождество после замены в нем неизвестных 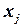 соответствующими числами
соответствующими числами 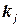 ,
, 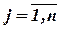 .
.
Несовместной называется система линейных уравнений, которая не имеет ни одного решения.
Совместной называется система линейных уравнений, которая обладает решениями.
Определенной называется совместная система линейных уравнений, если она обладает одним – единственным решением, а неопределенной, если решений больше, чем одно.
Неизвестные (переменные) в системе линейных уравнений могут быть представлены вектором размерности 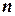 :
:
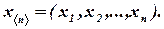
Тогда и решение системы линейных уравнений может быть представлено вектором той же размерности:
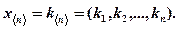
Решением неопределенной системы линейных уравнений является множество векторов.
Задача теории систем линейных уравнений состоит:
1) в установлении совместности системы линейных уравнений;
2) в установлении определенности совместной системы линейных уравнений;
3) в указании способа нахождения решений совместной системы линейных уравнений.
Вопросы для самопроверки
¨ Какие уравнения называются линейными?
¨ Что является решением системы линейных уравнений?
¨ Какая система линейных уравнений называется несовместной?
¨ Относятся ли определенная и неопределенная системы линейных уравнений к совместным?
¨ Может быть неопределенная система линейных уравнений несовместной?
¨ Чем отличаются между собой определенная и неопределенная системы линейных уравнений?
¨ В чем состоит задача теории систем линейных уравнений?
Решение определенной системы линейных уравнений
Матрицы и действия над ними
Матрицей из 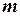 строк и
строк и 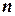 столбцов называется составленная из коэффициентов при неизвестных в системе линейных уравнений прямоугольная таблица
столбцов называется составленная из коэффициентов при неизвестных в системе линейных уравнений прямоугольная таблица
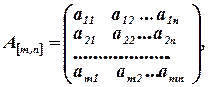
где 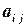 - элемент матрицы,
- элемент матрицы, 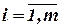 ,
, 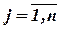 .
.
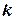 - мерным вектором называется упорядоченная система
- мерным вектором называется упорядоченная система 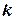 чисел:
чисел:
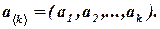

Компонентами (муж. род) вектора 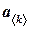 называются числа
называются числа 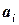 ,
, 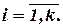
Строки матрицы 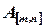 являются
являются 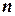 -мерными векторами
-мерными векторами 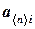 ,
, 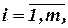 а столбцы -
а столбцы - 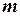 -мерными векторами
-мерными векторами 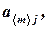
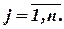
Любой вектор может быть представлен как матрица:
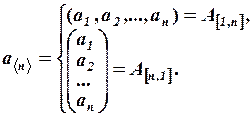
Действия над матрицами соответствуют действиям над векторами.
Суммой двух матриц 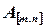 и
и 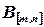 является матрица
является матрица 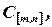 элементы которой есть сумма соответствующих элементов слагаемых матриц:
элементы которой есть сумма соответствующих элементов слагаемых матриц:
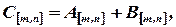
где 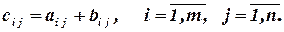
Суммируются матрицы только одинаковой размерности.
Произведением матрицы 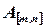 на число
на число 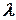 называется матрица
называется матрица 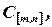 элементы которой есть произведения элементов матрицы
элементы которой есть произведения элементов матрицы 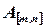 на число
на число 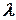 :
:
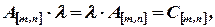
где 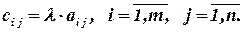
Произведением матрицы 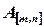 на матрицу
на матрицу 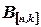 называется матрица
называется матрица 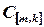 , каждый элемент которой есть сумма произведений соответствующих элементов из строки матрицы
, каждый элемент которой есть сумма произведений соответствующих элементов из строки матрицы 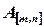 и из столбца матрицы
и из столбца матрицы 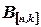 (по правилу “строка на столбец”):
(по правилу “строка на столбец”):
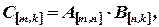
где 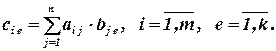
Умножаются первая матрица на вторую только в том случае, когда число столбцов первой матрицы равно числу строк второй матрицы. Получаемая в результате этого произведения матрица имеет столько же строк, сколько имеет первая матрица-сомножитель, и столько столбцов, сколько имеет вторая матрица-сомножитель.
▼
Примеры
Дано:
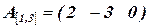 и
и 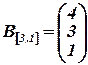 .
.
Найти 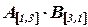 и
и 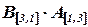 .
.
Решение:
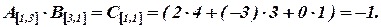
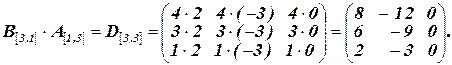
Дано:
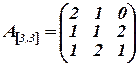 и
и 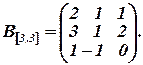
Найти 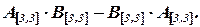
Решение:
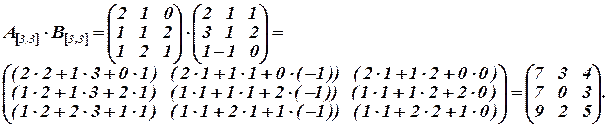
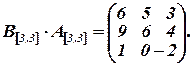
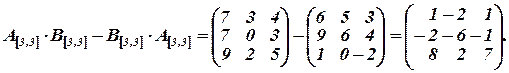
▲
Как правило, 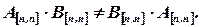
Матрица, у которой число строк равно числу столбцов, называется квадратной.
Квадратная матрица
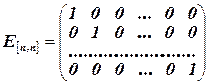
называется единичной.
Умножение на нее обладает следующими свойствами: