Простейшие понятия теории вероятностей
Раздел 12. Теория вероятностей.
1. Введение
2. Простейшие понятия теории вероятностей
3. Алгебра событий
4. Вероятность случайного события
5. Геометрические вероятности
6. Классические вероятности. Формулы комбинаторики.
7. Условная вероятность. Независимость событий.
8. Формула полной вероятности и формулы Байеса
9. Схема повторных испытаний. Формула Бернулли и её асимптотика
10. Случайные величины (СВ)
11. Ряд распределения ДСВ
12. Интегральная функция распределения
13. Функция распределения НСВ
14. Плотность вероятности НСВ
15. Числовые характеристики случайных величин
16. Примеры важных распределений СВ
16.1. Биномиальное распределение ДСВ.
16.2. Распределение Пуассона
16.3. Равномерное распределение НСВ.
16.4. Нормальное распределение.
17. Предельные теоремы теории вероятностей.
Введение
Теория вероятностей, подобно многим другим математическим дисциплинам, развивалась из потребностей практики. При этом, изучая реальный процесс, приходилось создавать абстрактную математическую модель реального процесса. Обычно учитывают главные, наиболее существенные движущие силы реального процесса, отбрасывая из рассмотрения второстепенные, которые называются случайными. Конечно, что считать главным, а что второстепенным,- отдельная задача. Решение этого вопроса определяет уровень абстракции, простоту или сложность математической модели и уровень адекватности модели реальному процессу. В сущности, любая абстрактная модель является результатом двух противостоящих устремлений: простоты и адекватности реальности.
Например, в теории стрельбы разработаны достаточно простые и удобные формулы для определения траектории полёта снаряда из орудия, расположенного в точке 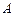 (рис. 1).
(рис. 1).
 |


 А
А
Рис.1
В определённых условиях упомянутая теория является достаточной, например, при массированной артподготовке.
Однако ясно, что если из одного орудия при одинаковых условиях произвести несколько выстрелов, то траектории будут хотя и близкими, но все же отличающимися. И если размер цели мал по сравнению с областью рассеивания, то возникают специфические вопросы, связанные именно с влиянием факторов, неучтённых в рамках предлагаемой модели. При этом учёт дополнительных факторов приведёт к слишком сложной модели, пользоваться которой практически невозможно. К тому же, этих случайных факторов бывает много, природа их чаще всего неизвестна.
В приведённом примере такими специфическими вопросами, выходящими за рамки детерминированной модели, являются, например, следующие: сколько надо произвести выстрелов, чтобы с определённой уверенностью (например, на 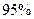 ) гарантировать поражение цели? как надо провести пристрелку, чтобы на поражение цели затратить наименьшее количество снарядов? и т.п.
) гарантировать поражение цели? как надо провести пристрелку, чтобы на поражение цели затратить наименьшее количество снарядов? и т.п.
Как мы увидим в дальнейшем, слова «случайный», «вероятность» станут строгими математическими терминами. Вместе с тем они весьма распространены в обычной разговорной речи. При этом считается, что прилагательное «случайный» является противопоставлением «закономерному». Однако, это не так, ибо природа устроена таким образом, что случайные процессы обнаруживают закономерности, но при определённых условиях.
Основное условие называется массовостью.
Например, если подбросить монету, то нельзя предсказать, что выпадает, герб или цифра,- можно лишь угадать. Однако, если эту монету подбросить большое число раз, что доля выпадений герба будет не сильно отличается от некоторого числа, близкого к 0,5 (в дальнейшем это число мы назовем вероятностью). Причем, с увеличением числа подбрасываний отклонение от этого числа будет уменьшаться. Это свойство называется устойчивостью средних показателей (в данном случае - доли гербов). Надо сказать, что на первых шагах теории вероятностей, когда надо было на практике убедиться в наличии свойства устойчивости, даже большие учёные не считали за труд провести самостоятельно проверку. Так, известен опыт Бюффона, который подбросил монету 4040 раз, и герб выпал 2048 раз, следовательно, доля (или относительная частота) выпадения герба равна 0,508, что близко интуитивно к ожидаемому числу 0,5.
Поэтому обычно даётся определение предмета теории вероятностей как раздела математики, изучающего закономерности массовых случайных процессов.
Надо сказать, что, несмотря на то, что наибольшие достижения теории вероятностей относятся к началу прошлого века, в особенности благодаря аксиоматическому построению теории в работах А.Н. Колмогорова (1903-1987), интерес к изучению случайностей проявился давно.
Сначала интересы были связаны с попытками применить числовой подход к азартным играм. Первые достаточно интересные результаты теории вероятностей принято связывать с работами Л. Пачоли (1494г), Д. Кардано (1526) и Н. Тартальи (1556).
Позже Б. Паскаль (1623-1662), П. Ферма (1601-1665), Х. Гюйгенс (1629-1695) заложили основы классической теории вероятностей. В начале 18 века Я. Бернулли (1654-1705) формирует понятие вероятности случайного события как отношение числа благоприятствующих шансов к числу всех возможных. На использовании понятия меры множества строили свои теории Э. Борель (1871-1956), А. Ломницкий (1881-1941), Р. Мизес (1883-1953).
Теоретико-множественная точка зрения в наиболее законченном виде была изложена в 1933г. А.Н. Колмогоровым в его монографии «Основные понятия теории вероятностей». Именно с этого момента теория вероятностей становится строгой математической наукой.
Большой вклад в развитие теории вероятностей внесли русские математики П.Л. Чебышёв (1821-1894), А.А. Марков (1856-1922), С.Н. Бернштейн (1880-1968) и другие.
Теория вероятностей бурно развивается и в настоящее время.
Простейшие понятия теории вероятностей
Как любая математическая дисциплина, теория вероятностей начинается с введения простейших понятий, которые не определяются, а лишь поясняются.
Одним из основных первичных понятий является опыт. Под опытом понимается некоторый комплекс условий, которые могут воспроизводиться неограниченное число раз. Каждую реализацию этого комплекса и назовем опытом или испытанием. Результаты опыта могут быть различными, в этом и проявляется элемент случайности. Различные результаты или исходы опыта называются событиями (точнее случайными событиями). Таким образом, при осуществлении опыта может произойти то или иное событие. Другими словами, случайное событие – это исход опыта, который при осуществлении опыта может произойти (появиться) или не произойти.
Опыт будем обозначать буквой 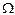 , а случайные события обозначаются обычно заглавными буквами
, а случайные события обозначаются обычно заглавными буквами 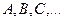
Часто в опыте можно заранее выделить его исходы, которые можно назвать простейшими, которые нельзя разложить на более простые. Такие события называются элементарными событиями (или случаями).
Пример 1. Пусть подбрасывается монета. Исходами опыта являются: выпадение герба (обозначим это событие буквой 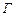 ); выпадение цифры (обозначим
); выпадение цифры (обозначим 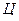 ). Тогда можно записать: опыт
). Тогда можно записать: опыт 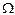 ={подбрасывание монеты}, исходы:
={подбрасывание монеты}, исходы: 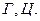 Ясно, что
Ясно, что 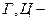 элементарные события в данном опыте. Иначе говоря, перечисление всех элементарных событий опыта полностью его описывает. По этому поводу будем говорить, что опыт есть пространство элементарных событий, и в нашем случае опыт кратко можно записать в виде:
элементарные события в данном опыте. Иначе говоря, перечисление всех элементарных событий опыта полностью его описывает. По этому поводу будем говорить, что опыт есть пространство элементарных событий, и в нашем случае опыт кратко можно записать в виде: 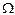 ={подбрасывание монеты}={Г;Ц}.
={подбрасывание монеты}={Г;Ц}.
Пример 2. 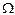 ={монета подбрасывается дважды}=
={монета подбрасывается дважды}= 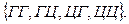 Здесь приведено словесное описание опыта и перечисление всех элементарных событий:
Здесь приведено словесное описание опыта и перечисление всех элементарных событий: 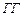 означает, что сначала при первом подбрасывании монеты выпал герб, при втором – тоже герб;
означает, что сначала при первом подбрасывании монеты выпал герб, при втором – тоже герб; 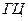 означает, что при первом подбрасывании монеты выпал герб, при втором цифра и т.д.
означает, что при первом подбрасывании монеты выпал герб, при втором цифра и т.д.
Пример 3. В системе координат 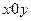 в квадрат
в квадрат 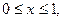
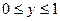 бросаются точки. В этом примере элементарными событиями являются точки с координатами
бросаются точки. В этом примере элементарными событиями являются точки с координатами 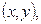 которые удовлетворяют приведенным неравенствам. Кратко это записывается следующим образом:
которые удовлетворяют приведенным неравенствам. Кратко это записывается следующим образом:
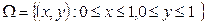 ,
,
Двоеточие в фигурных скобках означает, что 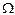 состоит из точек
состоит из точек 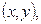 но не любых, а только тех, которые удовлетворяют условию (или условиям), указанным после двоеточия (в нашем примере это неравенства).
но не любых, а только тех, которые удовлетворяют условию (или условиям), указанным после двоеточия (в нашем примере это неравенства).
Пример 4. Монета подбрасывается до первого выпадения герба. Другими словами, подбрасывание монеты продолжается до тех пор, пока не выпадет герб. В этом примере элементарные события перечислить можно, хотя их бесконечное число:
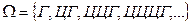
Заметим, что в примерах 3 и 4 пространство элементарных событий насчитывает бесконечное число исходов. В примере 4 их можно перечислить, т.е. пересчитать. Такое множество называется счетным. В примере 3 пространство 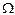 является несчетным.
является несчетным.
Введем в рассмотрение еще два события, которые присутствуют в любом опыте и которые имеют большое теоретические значение.
Назовем событие невозможным, если в результате опыта оно обязательно не произойдет. Будем его обозначать знаком пустого множества 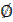 . Наоборот, событие, которое в результате опыта обязательно произойдёт называется достоверным. Достоверное событие обозначается так же, как и само пространство элементарных событий – буквой
. Наоборот, событие, которое в результате опыта обязательно произойдёт называется достоверным. Достоверное событие обозначается так же, как и само пространство элементарных событий – буквой 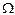 .
.
Например, при подбрасывании игральной кости событие {выпало меньше 9 очков} - достоверное, а событие {выпало ровно 9 очков} невозможное.
Итак, пространство элементарных событий может задаваться словесным описанием, перечислением всех его элементарных событий, заданием правил или условий, по которым получаются все его элементарные события.
Алгебра событий
До сих пор мы говорили лишь об элементарных событиях как непосредственных результатах опыта. Однако в рамках опыта можно говорить и о других случайных событиях, кроме элементарных.
Пример 5. При подбрасывании игральной кости, кроме элементарных событий 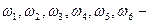 выпадений соответственно единицы, двойки,…, шестерки, можно говорить о других событиях:
выпадений соответственно единицы, двойки,…, шестерки, можно говорить о других событиях: 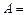 (выпадение четного числа),
(выпадение четного числа), 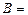 (выпадение нечетного числа),
(выпадение нечетного числа), 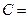 (выпадение числа, кратного трем),
(выпадение числа, кратного трем), 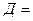 (выпадение числа, меньшего 4) и т.п. В данном примере указанные события, кроме словесного задания, можно задать перечислением элементарных событий:
(выпадение числа, меньшего 4) и т.п. В данном примере указанные события, кроме словесного задания, можно задать перечислением элементарных событий: 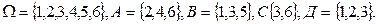
Образование новых событий из элементарных, а также из других событий осуществляется с помощью операций (или действий) над событиями.
Определение. Произведением 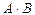 двух событий
двух событий 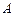 и
и 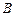 называется событие, состоящее в том, что в результате опыта произойдет и событие
называется событие, состоящее в том, что в результате опыта произойдет и событие 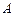 ,и событие
,и событие 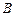 , т. е произойдут оба события вместе (одновременно).
, т. е произойдут оба события вместе (одновременно).
Знак произведения (точку) часто не ставят: 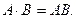
Определение. Суммой 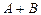 двух событий
двух событий 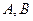 называется событие, состоящее в том, что в результате опыта произойдет или событие
называется событие, состоящее в том, что в результате опыта произойдет или событие 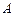 ,или событие
,или событие 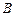 ,или оба вместе (одновременно).
,или оба вместе (одновременно).
В обоих определениях мы намеренно подчеркнули союзы и и или -сцелью привлечь внимание читателя к своей речи при решении задач. Если мы произносим союз «и», то речь идет о произведении событий; если произносится союз «или», то события надо складывать. При этом заметим что союз «или» в обиходной речи часто используется в смысле исключения одного из двух: «только 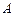 или только
или только 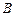 ». В теории вероятностей такое исключение не предполагается: и
». В теории вероятностей такое исключение не предполагается: и 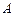 ,и
,и 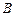 , и
, и 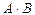 означают появление события
означают появление события 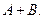
Если 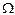 задано перечислением элементарных событий, то сложные события с помощью указанных операций получить просто. Для получения
задано перечислением элементарных событий, то сложные события с помощью указанных операций получить просто. Для получения 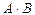 надо найти все элементарные события, принадлежащие обоим событиям, если таковых нет, то
надо найти все элементарные события, принадлежащие обоим событиям, если таковых нет, то 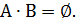 Сумму событий
Сумму событий 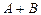 также составить несложно: надо взять любое из двух событий и добавить к нему те элементарные события из другого события, которые не входят в первое.
также составить несложно: надо взять любое из двух событий и добавить к нему те элементарные события из другого события, которые не входят в первое.
В примере 5 получаем, в частности 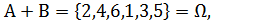
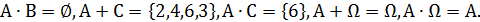
Введенные операции называются бинарными, т.к. определены для двух событий. Большое значение имеет следующая унарная операция (определенная для одного события): событие 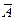 называется противоположным событию
называется противоположным событию 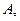 если оно состоит в том, что в данном опыте событие
если оно состоит в том, что в данном опыте событие 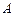 не произошло. Из определения ясно, что всякое событие
не произошло. Из определения ясно, что всякое событие 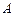 и ему противоположное
и ему противоположное 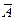 обладают следующими свойствами:
обладают следующими свойствами: 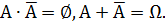 Введённая операция называется дополнением события А.
Введённая операция называется дополнением события А.
Отсюда следует, что если 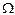 задано перечислением элементарных событий, то, зная задание события
задано перечислением элементарных событий, то, зная задание события 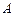 ,легко получить
,легко получить 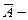 оно состоит из всех элементарных событий пространства
оно состоит из всех элементарных событий пространства 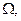 которые не принадлежат
которые не принадлежат 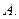 В частности, для примера 5 событие
В частности, для примера 5 событие 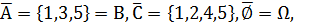
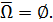 Если нет скобок, то устанавливается следующий приоритет в выполнении операций: дополнение, умножение, сложение.
Если нет скобок, то устанавливается следующий приоритет в выполнении операций: дополнение, умножение, сложение.
Итак, с помощью введённых операций пространство элементарных событий пополняется другими случайными событиями, которые образуют так называемую алгебру событий.
Пример 6. По мишени стрелок произвёл три выстрела. Рассмотрим события 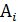 = {стрелок попал в мишень при i-м выстреле}, i = 1,2,3.
= {стрелок попал в мишень при i-м выстреле}, i = 1,2,3.
Составим из этих событий (не забудем и о противоположных 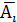 ) некоторые события. Пространных комментариев не приводим; полагаем, что читатель проведёт их самостоятельно.
) некоторые события. Пространных комментариев не приводим; полагаем, что читатель проведёт их самостоятельно.
Событие В = {все три выстрела попали в мишень}. Подробнее: В = {и первый, и второй, и третий выстрелы попали в мишень}. Использовали союз и, следовательно, события перемножаются: 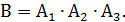
Аналогично:
С = {ни один из выстрелов не попал в цель} 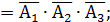
Е = {один выстрел достиг мишени} 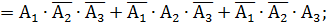
Д = {мишень поражена при втором выстреле} = 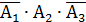 ;
;
F = {мишень поражена двумя выстрелами} 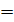
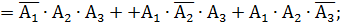
Н = {в мишени окажется хотя бы одно попадание} 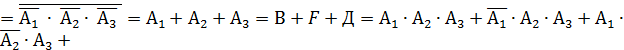
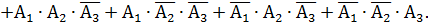
Как известно, в математике большое значение имеет геометрическая интерпретация аналитических объектов, понятий и формул.
В теории вероятностей удобно наглядное представление (геометрическая интерпретация) опыта, случайных событий и операций над ними в виде так называемых диаграмм Эйлера-Венна. Суть состоит в том, что всякий опыт отождествляется (интерпретируется) с бросанием точек в некоторый квадрат. Точки бросаются наугад, так что у всех точек имеются одинаковые шансы попасть в любое место этого квадрата. Квадрат определяет рамки рассматриваемого опыта. Каждое событие в рамках опыта отождествляется с некоторой областью квадрата. Иначе говоря, осуществление события 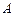 означает попадание случайной точки внутрь области, обозначенной буквой
означает попадание случайной точки внутрь области, обозначенной буквой 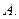 Тогда операции над событиями легко интерпретируются геометрически (рис.2)
Тогда операции над событиями легко интерпретируются геометрически (рис.2)
а) б)














|

 А:
А: 









 В:
В:
















 А
А  В:
В: 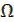
 А + В: всякая
А + В: всякая
штриховка
Рис.2
На рис.2 а) для наглядности событие А выделено вертикальной штриховкой, событие В - горизонтальной. Тогда операции умножения соответствует двойная штриховка - событию 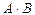 соответствует та часть квадрата которая покрыта двойной штриховкой. При этом, если
соответствует та часть квадрата которая покрыта двойной штриховкой. При этом, если 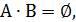 то
то 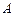 и
и 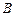 называются несовместными событиями. Соответственно операции сложения соответствует любая штриховка- событие
называются несовместными событиями. Соответственно операции сложения соответствует любая штриховка- событие 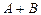 означает часть квадрата, заштрихованная любой штриховкой – вертикальной, горизонтальной и двойной. На рис.2 б) показано событие
означает часть квадрата, заштрихованная любой штриховкой – вертикальной, горизонтальной и двойной. На рис.2 б) показано событие 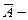 ему соответствует заштрихованная часть квадрата
ему соответствует заштрихованная часть квадрата 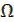 - все, что не входит в область
- все, что не входит в область 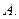 Введенные операции обладают следующими основными свойствами, некоторые из которых справедливы для одноименных операций над числами, но есть и специфические.
Введенные операции обладают следующими основными свойствами, некоторые из которых справедливы для одноименных операций над числами, но есть и специфические.
10. 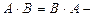 коммутативность умножения;
коммутативность умножения;
20. 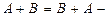 коммутативность сложения;
коммутативность сложения;
30. 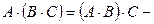 ассоциативность умножения;
ассоциативность умножения;
40. 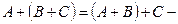 ассоциативность сложения,
ассоциативность сложения,
50. 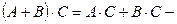 дистрибутивность умножения относительно сложения,
дистрибутивность умножения относительно сложения,
60. 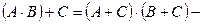 дистрибутивность сложения относительно умножения;
дистрибутивность сложения относительно умножения;
70. 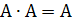
80. 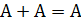
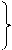 90.
90. 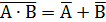 законы двойственности де Моргана,
законы двойственности де Моргана,
100. 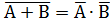
1 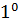 .A
.A 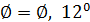 .A+
.A+ 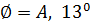 .A·
.A· 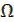 =A, 1
=A, 1 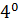 .A+
.A+ 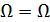 . 1
. 1 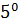 .A·
.A· 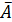 =
= 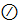 , 1
, 1 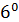 .A+
.A+ 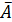 =
= 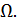
Пример 7. Иван и Петр договорились встретиться на временном промежутке в Т час, например , (0,Т). При этом они условились, что каждый из них, придя на встречу, ждет другого не более 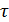 час.
час.
Придадим этому примеру геометрическую интерпретацию. Обозначим: 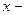 время прихода на встречу Ивана;
время прихода на встречу Ивана; 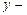 время прихода на встречу Петра. Согласно договоренности: 0
время прихода на встречу Петра. Согласно договоренности: 0 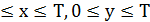 . Тогда в системе координат
. Тогда в системе координат 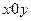 получаем:
получаем: 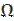 =
= 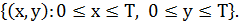 Нетрудно заметить, что в нашем примере пространство элементарных событий представляет собой квадрат.
Нетрудно заметить, что в нашем примере пространство элементарных событий представляет собой квадрат.
Далее введем событие 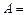 {встреча Ивана и Петра состоится}. По договоренности каждый из них, придя на встречу, ждёт не более
{встреча Ивана и Петра состоится}. По договоренности каждый из них, придя на встречу, ждёт не более 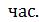 И если за эти
И если за эти 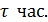 придет второй, то встреча состоится, т.е. встреча состоится если промежуток времени между приходами Ивана и Петра (или Петра и Ивана - смотря по тому, кто придет первым) будет меньше (или равен)
придет второй, то встреча состоится, т.е. встреча состоится если промежуток времени между приходами Ивана и Петра (или Петра и Ивана - смотря по тому, кто придет первым) будет меньше (или равен) 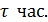 . Формально получаем: A=
. Формально получаем: A= 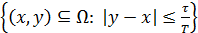 .
.
Изобразим 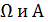 на чертеже (рис.3.)
на чертеже (рис.3.)

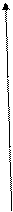 y
y

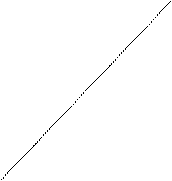


 1
1
 | |||
 |



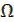 A
A





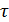

 0
0 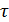 x
x
Рис.3
Для построения области, соответствующей событию 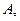 т.е. той части квадрата, которая удовлетворяет неравенству, распишем это неравенство в виде двойного неравенства:
т.е. той части квадрата, которая удовлетворяет неравенству, распишем это неравенство в виде двойного неравенства:
-  ≤y -x≤
≤y -x≤ 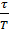
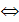 x -
x -  ≤y≤ x+
≤y≤ x+  .
.
Всегда для того, чтобы выявить точки, удовлетворяющие неравенству, начинаем с равенства, т.е. с уравнения. Поэтому рассмотрим уравнение, соответствующее левой части двойного неравенства: y=x – 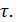 Это уравнение 1-й степени - уравнение прямой, параллельной биссектрисе 1-го координатного угла и сдвинутой вниз на
Это уравнение 1-й степени - уравнение прямой, параллельной биссектрисе 1-го координатного угла и сдвинутой вниз на 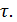 Эта прямая делит всю плоскость (а нас интересует только квадрат) на две части. Неравенству y≥x –
Эта прямая делит всю плоскость (а нас интересует только квадрат) на две части. Неравенству y≥x – 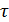 соответствует та часть квадрата, которая расположена выше этой прямой.Аналогично, второму неравенству y≤x+
соответствует та часть квадрата, которая расположена выше этой прямой.Аналогично, второму неравенству y≤x+ 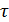 соответствует нижняя часть квадрата относительно прямой а двойному неравенству, т.е. событию
соответствует нижняя часть квадрата относительно прямой а двойному неравенству, т.е. событию 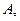 соответствуют точки квадрата, расположенные между этими прямыми (см. рис.3).
соответствуют точки квадрата, расположенные между этими прямыми (см. рис.3).
Пример 8. Рассмотрим две электрические схемы, состоящие из трех элементов 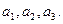 Схема
Схема 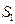 представляет собой последовательное соединение элементов, а схема
представляет собой последовательное соединение элементов, а схема 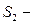 параллельное (рис.4).
параллельное (рис.4).
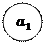
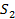



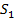
 |  | ||||
 |
Рис.4
Обозначаем события 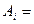 {элемент
{элемент 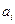 работает},
работает}, 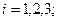
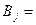 {схема
{схема 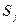 работает},
работает}, 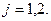 Требуется выразить события
Требуется выразить события 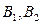 через
через 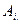
Из физики известно, что схема 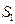 работает, если работают (исправны) все элементы (и
работает, если работают (исправны) все элементы (и 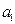 и
и 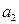 и
и 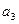 ), следовательно,
), следовательно, 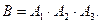 Заметим, что из физики также известно, что схема
Заметим, что из физики также известно, что схема 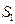 не работает, если откажет хотя бы один элемент этой схемы, т.е. или какой-нибудь один , или какие-нибудь два, или все три, т.е.
не работает, если откажет хотя бы один элемент этой схемы, т.е. или какой-нибудь один , или какие-нибудь два, или все три, т.е. 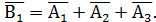 Таким образом, в физике закон двойственности де Моргана:
Таким образом, в физике закон двойственности де Моргана: 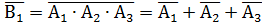 реализуется в последовательном соединении элементов.
реализуется в последовательном соединении элементов.
Аналогичная ситуация имеет место и для схемы 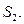 При параллельном соединении схема работает, если работает по крайней мере (хотя бы) один элемент, т.е.
При параллельном соединении схема работает, если работает по крайней мере (хотя бы) один элемент, т.е. 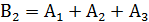 ; и не работает, если не работают все элементы, т.е.
; и не работает, если не работают все элементы, т.е. 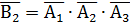 .Таким образом, второй закон двойственности де Моргана:
.Таким образом, второй закон двойственности де Моргана: 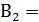
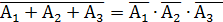 реализуется при параллельном соединении элементов.
реализуется при параллельном соединении элементов.
Приведённый пример показывает, почему теория вероятностей находит большое применение в физике, в частности, в расчетах надежности реальных технических устройств.