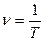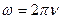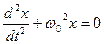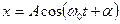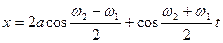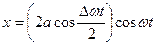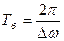Колебания. Характеристики гармонических колебаний
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
План
1. Колебания. Характеристики гармонических колебаний.
2. Свободные (собственные) колебания. Дифференциальное уравнение гармонических колебаний и его решение. Гармонический осциллятор.
3. Энергия гармонических колебаний.
4. Сложение одинаково направленных гармонических колебаний. Биение. Метод векторной диаграммы.
5. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.
6. Затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение. Частота затухающих колебаний. Изохронность колебаний. Коэффициент, декремент, логарифмический декремент затухания. Добротность колебательной системы.
7. Вынужденные механические колебания. Амплитуда и фаза вынужденных механических колебаний.
8. Механический резонанс. Соотношение между фазами вынуждающей силы и скорости при механическом резонансе.
9. понятие об автоколебаниях.
Колебания. Характеристики гармонических колебаний.
Колебания – движение или процессы, обладающие той или иной степенью повторности во времени.
Гармонические (или синусоидальные) колебания – разновидность периодических колебаний, которые могут быть заменены в виде
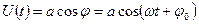 (1)
(1)
где a – амплитуда, 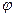 - фаза,
- фаза, 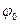 - начальная фаза,
- начальная фаза, 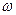 - циклическая частота, t – время (т.е. применяются со временем по закону синуса или косинуса).
- циклическая частота, t – время (т.е. применяются со временем по закону синуса или косинуса).
Амплитуда (а) – наибольшее отклонение от среднего значения величины, совершающей колебания.
Фаза колебаний ( ) 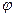 – изменяющийся аргумент функции, описывающей колебательный процесс (величина
– изменяющийся аргумент функции, описывающей колебательный процесс (величина 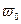 t+
t+ 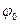 , стоящая под знаком синуса в выражении (1) ).
, стоящая под знаком синуса в выражении (1) ).
Фаза характеризует значение изменяющейся величины в данный момент времени. Значение 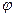 в момент времени t=0 называется начальной фазой (
в момент времени t=0 называется начальной фазой ( 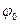 ).
).
В качестве примера на рисунке 27.1 представлены математические маятники в крайних положениях с разностью фаз колебаний 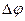 =0 (27.1.а) и
=0 (27.1.а) и 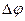 =
= 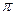 (27.1б)
(27.1б)
 |
Разность фаз колебаний маятников проявляется отличием в положении колеблющихся маятников.
Циклической или круговой частотой называется количество колебаний, совершаемое за 2 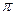 секунд.
секунд.
Частотой колебаний 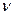 (или линейной частотой) называется число колебаний в единицу времени. За единицу частоты принимается частота таких колебаний, период которых равен 1с. Эту единицу называют Герц (Гц).
(или линейной частотой) называется число колебаний в единицу времени. За единицу частоты принимается частота таких колебаний, период которых равен 1с. Эту единицу называют Герц (Гц).
Промежуток времени, за который совершается одно полное колебание, а фаза колебания получает приращение, равное 2 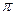 , называется периодом колебания (рис. 27.2).
, называется периодом колебания (рис. 27.2).


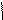
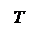
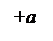 Частота
Частота 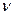 связана с пе-
связана с пе-
 риодом Т соотношении-
риодом Т соотношении-
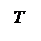 ем
ем

|
|

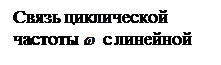
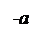

|
рис. 27.2
2. Свободные колебания. Свободными или собственными называются такие колебания, которые происходят в системе, выведенной из положения равновесия и предоставленной самой себе.
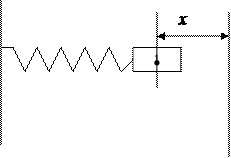
Рассмотрим колебания груза на пружине, совершаемые на гладкой горизонтальной поверхности (рис. 27.3). Если растянуть пружину на некоторое расстояние х, и затем отпустить, то на груз будет действовать упругая
 |

 | |||
| |||
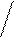
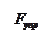
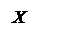









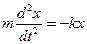 .
.
Поделив обе части уравнений на m
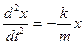
и перенеся в левую часть
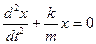 .
.
Обозначив 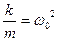 , получим линейное дифференциальное однородное уравнение второго порядка
, получим линейное дифференциальное однородное уравнение второго порядка
|
(линейное – т.е. и сама величина х, и ее производная в первой степени; однородное – т.к. нет свободного члена, не содержащего х ; второго порядка – т.к. вторая производная х).
Уравнение (2) решается (*) подстановкой х = 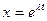 . Подставляя в (2) и проводя дифференцирование
. Подставляя в (2) и проводя дифференцирование
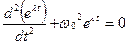
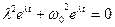 .
.
Получаем характеристическое уравнение
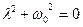 .
.
Это уравнение имеет мнимые корни: 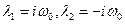 (
( 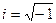 -мнимая единица).
-мнимая единица).
Общее решение имеет вид
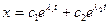
где 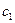 и
и 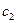 - комплексные постоянные.
- комплексные постоянные.
Подставляя корни, получим
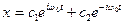 (3)
(3)
(Замечание: комплексным числом z называется число вида z = x + iy, где x,y – вещественные числа, i – мнимая единица ( 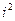 = -1). Число х называется вещественной частью комплексного числа z.. Число у называется мнимой частью z).
= -1). Число х называется вещественной частью комплексного числа z.. Число у называется мнимой частью z).

 (*) В сокращенном варианте решение можно опустить
(*) В сокращенном варианте решение можно опустить
Выражение вида 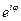 можно представить в виде комплексного числа с помощью формулы Эйлера
можно представить в виде комплексного числа с помощью формулы Эйлера
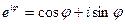
аналогично
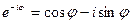
(т.к. 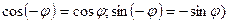 .
.
Положим 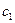 и
и 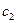 в виде комплексных постоянных
в виде комплексных постоянных 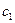 = А
= А 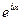 , а
, а 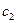 = А
= А 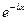 , где А и
, где А и 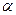 произвольные постоянные. Из (3) получим
произвольные постоянные. Из (3) получим
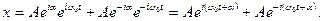
Обозначив 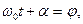 получим
получим
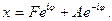
Используя формулу Эйлера
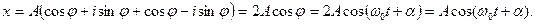
|
(4)
где 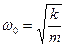 - собственная круговая частота колебаний, А – амплитуда.
- собственная круговая частота колебаний, А – амплитуда.
Смещение х применяется со временем по закону косинуса, т.е. движение системы под действием упругой силы f = -кх представляет собой гармоническое колебание.
Если величины, описывающие колебания некоторой системы периодически изменяются со временем, то для такой системы пользуются термином «осциллятор».
Линейным гармоническим осциллятором называется такой, движение которого описывается линейным уравнением 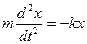 .
.
3. Энергия гармонических колебаний. Полная механическая энергия системы, изображенной на рис. 27.2 равна сумме механической и потенциальной энергий.
Продифференцируем по времени выражение ( 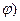 , получим
, получим
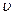 =
= 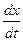 = -a
= -a 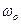 sin(
sin( 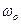 t +
t + 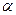 ).
).
Кинетическая энергия груза (массой пружины пренебрегаем) равна
E 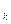 =
= 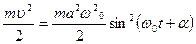 .
.
Потенциальная энергия выражается известной формулой 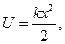 подставляя х из (4), получим
подставляя х из (4), получим
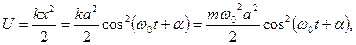 т.к.
т.к. 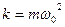 .
.
Полная энергия
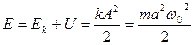
величина постоянная. В процессе колебаний потенциальная энергия переходит в кинетическую и наоборот, но каждая энергия остается неизменной.
4. Сложение одинаково направленных колебаний.. Обычно одно и то же тело участвует в нескольких колебаниях. Так, например, звуковые колебания, воспринимаемые нами при слушании оркестра представляют собой сумму колебаний воздуха, вызываемых каждым из музыкальных инструментов в отдельности.
Рассмотрим сложение двух гармонических колебаний одинакового направления. Смещение х колеблющегося тела будет суммой смещений 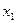 и
и 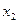 . Положим равными, для простоты, амплитуды
. Положим равными, для простоты, амплитуды 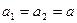 и начальные фазы
и начальные фазы 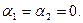 Тогда
Тогда
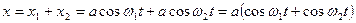 .
.
Воспользовавшись формулой суммы косинусов, получим
|
(5)
Биения. Пусть два складываемых гармонических колебания одинакового направления мало отличаются по частоте. Обозначим частоту одного из колебаний 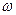 , частоту второго
, частоту второго 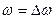 . При этом
. При этом 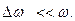 Амплитуды обоих колебаний будем полагать одинаковыми и равными а. Начальные фазы для упрощения задачи положим равными нулю. Тогда
Амплитуды обоих колебаний будем полагать одинаковыми и равными а. Начальные фазы для упрощения задачи положим равными нулю. Тогда
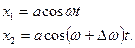
Сложим эти колебания, воспользовавшись формулой (5), получим
|
(6)
Во втором сомножителе (6) пренебрегли 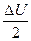 по сравнению с
по сравнению с 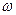 . Множитель
. Множитель 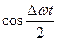 меняется гораздо медленнее, чем
меняется гораздо медленнее, чем 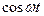 (т.к.
(т.к. 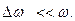 ). Результирующее колебание х можно рассматривать как гармоническое с частотой
). Результирующее колебание х можно рассматривать как гармоническое с частотой 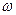 , амплитуда которого меняется по закону
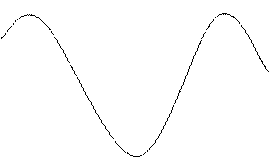
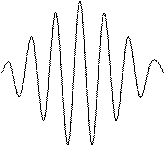
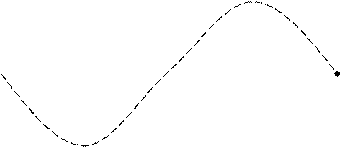
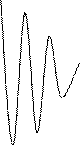
, амплитуда которого меняется по закону 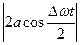 от -2а до +2а (амплитуда – величина положительная). Такие колебания называются биениями. Они представлены на рис.27.4.
от -2а до +2а (амплитуда – величина положительная). Такие колебания называются биениями. Они представлены на рис.27.4.
 |
|
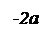
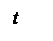


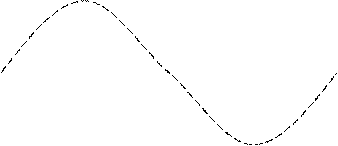

Частота пульсаций амплитуды называется частотой биений.Промежуток времени между соседними моментами времени, когда амплитуда максимальна, называется периодом биений Тб. За это время разность фаз изменяется на 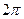 , т.е.
, т.е.
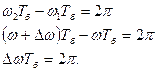
Таким образом период биений
|