Метод решения несобственного интеграла с точкой разрыва на отрезке интегрирования

Такие примеры встречаются на практике относительно редко, поэтому ограничимся только обзором. Пример опять же будет, в известной степени, условным. Рассмотрим несобственный интеграл

.

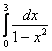На концах отрезка интегрирования всё хорошо. Но подынтегральная функция терпит бесконечный разрыв прямо на отрезке в точке x = 1. Подынтегральная функция является четной, но это не имеет никакого значения, поскольку отрезок интервал интегрирования не симметричен относительно нуля.

Метод решения – тот же старый. Представим несобственный интеграл в виде суммы двух несобственных интегралов:

.

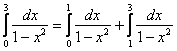Интегралы правой части вам уже знакомы.

Решения и ответы:

Пример 2: Решение:

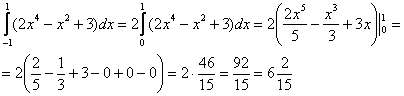
Пример 5: Решение:

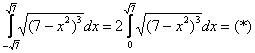
Проведем замену:

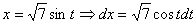
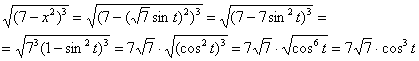
Новые пределы интегрирования:

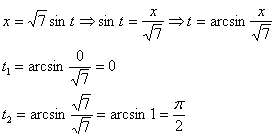
Пример 8: Решение:

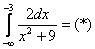
Подынтегральная функция непрерывна на интервале .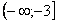

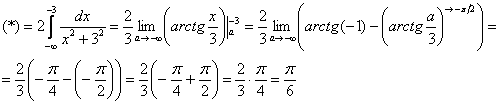
Пример 11: Решение:

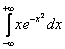
Подынтегральная функция непрерывна на всей числовой прямой. Представим интеграл в виде суммы двух интегралов:

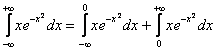
Проверим сходимость интегралов правой части:

Сходится.

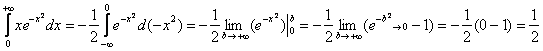
Сходится. Оба интеграла сходятся, значит, сходится и весь интеграл:

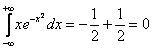
Ответ:

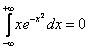
Примечание: Будет серьезной оплошностью сразу записать, что

,

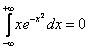пользуясь нечетностью подынтегральной функции и симметричностью интервала интегрирования. Стандартный алгоритм обязателен!!!

Пример 13: Решение:

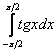
Подынтегральная функция терпит бесконечные разрывы в точках

.

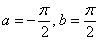Представим данный интеграл в виде суммы двух интегралов:

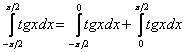
Исследуем сходимость интегралов правой части:

Несобственный интеграл расходится, значит, расходится и весь интеграл.

Интеграл

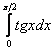- можно уже не проверять.

Ответ:интеграл

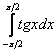– расходится

Приложение 1. Числа

Наиболее общие закономерности и законы экономических явлений выясняются путем качественного анализа, но конкретное выражение их возможно лишь с помощью меры и числа.

Число - важнейшее математическое понятие, меняющееся на протяжении веков. Первые представления о числе возникли из счета людей, животных, плодов, различных изделий и пр. Результатом являются натуральные числа: 1, 2, 3, 4…

При счете отдельных предметов единица есть наименьшее число, и делить ее на доли не нужно, а иногда и нельзя, однако уже при грубых измерениях величин приходится делить 1 на доли.

Исторически первым расширением понятия числа является присоединение к натуральному числу дробных чисел.

Дробью называется часть (доля) единицы или несколько равных ее частей.

Дроби обозначаются, как 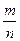; где m и n - целые числа.

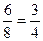- это сокращение дроби; а 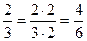- это расширение дроби.

Дроби со знаменателем 10 - это десятичные дроби, которые обозначаются с помощью запятой, разделяющей целую и дробную части: .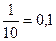

Среди десятичных дробей особое место занимают периодические дроби.

Различают 2 случая:

1) чистая периодическая дробь, как 0,2525…=0,(25)= ;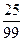

2) смешанная периодическая дробь, как 1,2555…=1,2(5)= .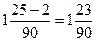

Дальнейшее расширение понятия числа вызвано уже развитием самой математики. Рене Декарт в 17 веке ввёл понятие отрицательного числа. Объединение множеств целых (положительных и отрицательных) чисел, дробных (положительных и отрицательных) чисел и нуля получили название рациональных чисел (rational numbers).

Определение: Всякое рациональное число может быть записано в виде отношения двух целых чисел, одно из которых (в знаменателе) не равно нулю.

Определение: Всякое рациональное число может быть записано в виде конечной дроби (с конечным числом знаков после запятой) или периодической дроби.

Для изучения непрерывно изменяющихся переменных величин оказалось необходимым новое расширение понятия числа - ввели действительные (вещественные) числа (real numbers).

Объединение множеств рациональных (положительных и отрицательных) и иррациональных (положительных и отрицательных) чисел получило название множества действительных чисел.

Определение: Всякое иррациональное число может быть записано в виде бесконечной десятичной непериодической дроби.

Иррациональные числа (irrational numbers) появились при измерении несоизмеримых отрезков (таких, как сторона и диагональ квадрата).

В алгебре иррациональные числа появились при извлечении корней 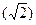. Примером трансцендентного, или иррационального числа являются числа π, е.

Все действительные числа можно изобразить на числовой оси.

Числовая ось(числовая прямая) это:

а) прямая линия с выбранным на ней направлением;

б) на оси задано начало отсчета – нулевая точка (0);

в) на оси задана единица масштаба.

Х

-2 -1 1 2 3

Комплексные числа.После действительных чисел (real numbers) не появилось «недействительных чисел», но возникли так называемые «комплексные числа» (complex numbers). «Комплексное число» - это не число в обычном понимании, характеризующееся одним параметром, а математический объект, составленный из двух элементов, каждый из которых - действительное число.

Геометрически комплексное число может быть представлено, как точка на плоскости (элемент плоскости), на которой задана прямоугольная система координат: две взаимно перпендикулярные числовые оси (0X и 0Y) с общей нулевой точкой (0) начала отсчёта. Произвольная точка такой координатной плоскости определяется упорядоченной парой чисел (x; y), где x и y называют обычно координатами точки по соответствующим осям. Пара называется упорядоченной, т. к. при перестановке чисел x; y местами в скобках получается другое комплексное число (другая пара): (x; y) ¹ (y; x).

Определение: Всякое комплексное число представимо в виде упорядоченной пары действительных чисел: z =(x; y), где и x, и y – действительные числа, а z – «название» этой пары. Причём первое в паре число (x) называют действительной частью комплексного числа, а второе в паре число (y) – мнимой частью комплексного числа.

Действительные числа после этого определения стали обозначать, как x º (x; 0), и отмечать их на числовой оси 0X, а мнимые числа (мнимые части комплексных чисел) – как y º (0; y). Для комплексных чисел ввели особые алгебраические операции. Оказалось, что комплексные числа представимы в виде векторов и просто «алгебраически», как: z = x + i∙y, если величину i º (0; 1) назвать мнимой единицей (смотрите раздел Комплексные числа).