Базисные функции вейвлет-преобразования /1, 3/
ВЕЙВЛЕТНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
Wavelet transformations of signals
Тема 20. СВОЙСТВА ВЕЙВЛЕТ-преобразования
Изложение вопроса будет неполным, пока в той или иной форме мы не оговорим всех условий.
Джон Стюарт Милль. Английский философ, XIX в.
Оговорить можно. Только если в этих условиях не потонет смысл самого вопроса.
Игорь Широков. Московский геофизик Уральской школы, XX в.
Содержание
Введение.
1. Базисные функции вейвлет-преобразования. Определение вейвлета. Свойства вейвлета. Отображение преобразования. Вейвлетные функции.
2. Свойства вейвлет-преобразования.
3. Вейвлет-преобразование простых сигналов.
Введение.
Аналитика вейвлетных преобразований сигналов определяются математической базой разложения сигналов, которая аналогична преобразованиям Фурье. Основной отличительной особенностью вейвлет-преобразований является новый базис разложения сигналов - вейвлетные функции. Свойства вейвлетов принципиально важны как для самой возможности разложения сигналов по единичным вейвлетным функциям, так и для целенаправленных действий над вейвлетными спектрами сигналов, в том числе с последующей реконструкцией сигналов по обработанным вейвлетным спектрам.
Вейвлеты могут быть ортогональными, полуортогональными, биортогональными. Эти функции могут быть симметричными, асимметричными и несимметричными, с компактной областью определения и не имеющие таковой. Некоторые функции имеют аналитическое выражение, другие – быстрый алгоритм вычисления вейвлет-преобразования. Вейвлеты различаются также степенью гладкости. Для практики желательно было бы иметь ортогональные симметричные и асимметричные вейвлеты. К сожалению, такими вейвлетами являются лишь вейвлеты Хаара, которые не обладают достаточной гладкостью и не подходят для большинства приложений. Наибольшее применение находят биортогональные вейвлеты.
Базисные функции вейвлет-преобразования /1, 3/.
Базисными функциями вейвлет-преобразований, которые собственно и называются вейвлетами, могут быть самые различные функции с компактным носителем - модулированные импульсами синусоиды, функции со скачками уровня и т.п. Они обеспечивает хорошее отображение и анализ сигналов с локальными особенностями, в том числе со скачками, разрывами и перепадами значений с большой крутизной, при подборе соответствующего типа вейвлетов.
Следует, однако, различать вейвлеты по целевым задачам вейвлетных преобразований с позиций декомпозиции – реконструкции сигналов. По аналогии с преобразованием Фурье, было бы желательно иметь такое вейвлет-преобразование сигналов, которое обеспечивало бы полную информационную эквивалентность нового представления сигналов (вейвлетного спектра) временному (динамическому, координатному) представлению, и, соответственно, однозначность как декомпозиции сигналов, так и их реконструкции из вейвлетных спектров. Однако это возможно только при использовании ортогональных базисных функций, к числу которых относится достаточно ограниченное количество ортогональных и биортогональных вейвлетов. Этим вейвлетам и будет уделено основное внимание. Вместе с тем для качественного анализа сигналов и локальных особенностей в сигналах может применяться гораздо более обширная номенклатура вейвлетных функций, которые хотя и не обеспечивают реконструкцию сигналов, но позволяют по новому оценить информационное содержание сигналов и динамику изменения этой информации.
Определение вейвлета.В общем случае к вейвлетам относятся локализованные функции, которые конструируются из одного материнского вейвлета y(t) (или по любой другой независимой переменной) путем операций сдвига по времени (b) и изменения временного масштаба (а):
yab(t) = (1/ 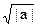 ) y((t-b)/a), (a, b)ÎR, y(t)ÎL2(R).
) y((t-b)/a), (a, b)ÎR, y(t)ÎL2(R).
где множитель (1/ 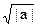 ) обеспечивает независимость нормы функций от масштабирующего числа 'a'.
) обеспечивает независимость нормы функций от масштабирующего числа 'a'.
Непрерывное (интегральное) вейвлет-преобразование сигнала s(t)ÎL2(R), которое применяется для качественного частотно-временного анализа, по смыслу соответствует преобразованию Фурье с заменой гармонического базиса exp(-jwt) на вейвлетный y((t-b)/a):
W(a, b) = ás(t), yab(t)ñ = (1/ 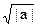 )
) 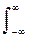 s(t) y((t-b)/a) dt, (a, b)ÎR, a¹0.
s(t) y((t-b)/a) dt, (a, b)ÎR, a¹0.
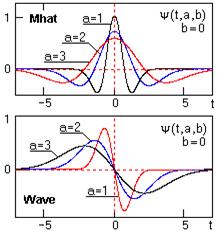 Рис. 2.1.1. Вейвлеты Mhat и Wave. Рис. 2.1.1. Вейвлеты Mhat и Wave. |
Вейвлетный масштабно-временной спектр W(a,b) в отличие от фурье-спектра является функцией двух аргументов: временного масштаба вейвлета 'а' (в единицах, обратных частоте), и временному смещению вейвлета по сигналу 'b' (в единицах времени), при этом параметры 'а' и 'b' могут принимать любые значения в пределах областей их определения.
На рис. 2.1.1 приведены примеры простейших неортогональных вейвлетов четного (Mhat) и нечетного (Wave) типов.
Для количественных методов анализа (декомпозиция сигналов с возможностью последующей линейной реконструкции сигналов из обработанных вейвлет-спекторов) строго с математических позиций в качестве вейвлетных базисов можно использовать любые локализованные функции y(t)Î L2(R), если для них существуют функции-двойники (парные функции) y#(t), такие, что семейства {yab(t)} и {y#ab(t)} могут образовывать парные базисы функционального пространства L2(R). Вейвлеты, определенные таким образом, позволяют представить любую произвольную функцию в пространстве L2(R) в виде ряда:
s(t) = 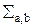 С(a,b) y#ab(t), (a, b)ÎI,
С(a,b) y#ab(t), (a, b)ÎI,
где коэффициенты С(a,b) – проекции сигнала на вейвлетный базис пространства, которые определяются скалярным произведением
С(a,b) = ás(t), yab(t)ñ = 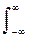 s(t) yab(t) dt.
s(t) yab(t) dt.
Если вейвлет y(t) обладает свойством ортогональности, то y#(t) ≡ y(t) и вейвлетный базис ортогонален. Вейвлет может быть неортогональным, однако если он имеет двойника, и пара (y(t), y#(t)) дает возможность сформировать семейства {ymk(t)} и {y#zp(t)}, удовлетворяющие условию биортогональности на целых числах I:
áymk(t), y#zp(t)ñ = dmz·dkp, m,k,z,p Î I,
то возможно разложение сигналов на вейвлетные ряды с построением обратной формулы реконструкции. С точностью обратного вейвлет-преобразования связано большинство ограничений, накладываемых на вейвлеты.
Свойства вейвлета, которые принципиально важны для реализации вейвлетных преобразований:
· Локализация. Вейвлет должен быть непрерывным, интегрируемым, иметь компактный носитель и быть локализованным как во времени (в пространстве), так и по частоте. Если вейвлет в пространстве сужается, то его "средняя" (доминирующая) частота повышается, спектр вейвлета перемещается в область более высоких частот и расширяется. Этот процесс должен быть линейным – сужение вейвлета вдвое должно повышать его доминирующую частоту и ширину спектра также вдвое.
Вейвлетную функцию можно считать достаточно хорошо локализованной при выполнении условий:
y(t) ≤ C/(1+|t|)1+e, Y(f) ≤ C/(1+|f|)1+e, при e > 0.
· Нулевое среднее значение, т.е. выполнение условия для нулевого момента:
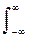 y(t) dt = 0,
y(t) dt = 0,
что обеспечивает выделение локальных особенностей сигналов в пределах вейвлетного носителя на уровне региональных изменений и тренда, нулевое усиление постоянной составляющей сигналов с нулевым значением частотного спектра вейвлета при w=0, и локализацию спектра вейвлета в виде полосового фильтра с центром на определенной (доминирующей) частоте w0 вейвлетной функции. Для игнорирования регулярных полиномиальных составляющих сигнала и анализа мелкомасштабных флюктуаций и особенностей высокого порядка, как правило, требуются и нулевые значения определенного количества последующих моментов:
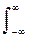 tm y(t) dt = 0.
tm y(t) dt = 0.
Такие вейвлеты называются вейвлетами m-го порядка.
· Ограниченность. Необходимое и достаточное условие:
||y(t)||2 = 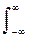 |y(t)|2 dt < ¥
|y(t)|2 dt < ¥
Оценка хорошей ограниченности и локализации может выполняться с использованием выражений:
|y(t)| < 1/(1+|t|n), или |Y(ω)| < 1/(1+|ωo|n).
где wo – средняя частота вейвлета. Число n должно быть как можно больше.
· Автомодельность базиса или самоподобие. Форма всех базисных вейвлетов yab(t) должна быть подобна материнскому вейвлету y(t), т.е. должна оставаться одной и той же при сдвигах и масштабировании (растяжении/сжатии), иметь одно и то же число осцилляций.
Отображение преобразования. Результатом вейвлет-преобразования одномерного числового ряда (сигнала) является двумерный массив значений коэффициентов С(a,b). Распределение этих значений в пространстве (a,b) - временной масштаб, временная локализация, дает информацию об изменении во времени относительного вклада в сигнале вейвлетных компонент разного масштаба и называется спектром коэффициентов вейвлет-преобразования, масштабно-временным (частотно-временным) спектром или просто вейвлет-спектром (wavelet spectrum).
Спектр C(a,b) одномерного сигнала представляет собой поверхность в трехмерном пространстве. Способы визуализации спектра могут быть самыми различными. Наиболее распространенный способ – проекция на плоскость ab с изолиниями (изоуровнями), что позволяет проследить изменения коэффициентов на разных масштабах во времени, а также выявить картину локальных экстремумов этих поверхностей ("холмов" и "впадин"), так называемый "скелет" (skeleton) структуры анализируемого процесса. При широком диапазоне масштабов применяются логарифмические координаты (log a, b). Пример вейвлетного спектра простейшего сигнала при его разложении вейвлетом Mhat приведен на рис. 2.1.2.

Рис. 2.1.2. Сигнал, вейвлетный Mhat - спектр и масштабные сечения спектра.
По вертикальным сечениям (сечениям сдвига b) вейвлет-спектр отражает компонентный состав сигнала (из данного комплекта вейвлетов) в каждый текущий момент. По смыслу преобразования, как скалярного произведения сигнала с вейвлетом, ясно, что значения коэффициентов в каждой текущей временной точке по масштабным сечениям тем больше, чем сильнее корреляция между вейвлетом данного масштаба и поведением сигнала в окрестностях этой точки. Соответственно, масштабные сечения по параметру 'а' демонстрируют изменения в сигнале компоненты данного масштаба 'a' со временем.
Заметим, что вейвлетные составляющие сигнала в сечениях его спектра не имеют ничего общего с синусоидами, и представлены, как правило, сигналами достаточно сложной и не всегда понятной формы, что может затруднять их наглядное представление и понимание. Примеры отображения вейвлет-преобразований для различных типов сигналов приводятся ниже.
Вейвлетные функции.Выбор анализирующего вейвлета во многом определяется тем, какую информацию необходимо извлечь из сигнала. С учетом характерных особенностей различных вейвлетов во временном и в частотном пространстве, можно выявлять в анализируемых сигналах те или иные свойства и особенности, которые незаметны на графиках сигналов, особенно в присутствии сильных шумов. При этом задача реконструкции сигнала может и не ставится, что расширяет семейство используемых регулярных и симметричных вейвлетных функций. Более того, вейвлет может конструироваться непосредственно под ту локальную особенность в сигнале, которая подлежит выделению или обнаружению, если ее форма априорно известна.
При анализе сигналов вейвлетами четного типа (симметричными или близкими к симметричным) гармоническим сигналам обычно соответствуют яркие горизонтальные полосы вейвлетных пиков и впадин на доминирующих частотах вейвлетов, совпадающих с частотой гармоник сигналов. Нарушения гладкости сигналов фиксируются вертикальными полосами, пики в сигналах выделяются максимумами, а впадины – минимумами вейвлетных коэффициентов. Напротив, вейвлеты нечетного типа более резко реагируют на скачки и быстрые изменения в сигналах, отмечая их максимумами или минимумами в зависимости от знака дифференциалов. Чем резче выражены особенности сигналов, тем сильнее они выделяются на спектрограммах.
Для конструирования таких вейвлетов часто используются производные функции Гаусса, которая имеет наилучшую локализацию как во временной, так и в частотной областях. В общей форме уравнение базового вейвлета:
yn(x) = (-1)n+1 dn[exp(-x2/2)]/dxn, n ≥ 1, (2.1.1)
Уравнения базовых вейвлетов для первых четырех производных:
y1(x) = -x exp(-x2/2), y2(x) = (1-x2) exp(-x2/2),
y3(x) = (3x-x3) exp(-x2/2), y4(x) = (-4x4+6x2-3) exp(-x2/2),
Уравнения нормированных базисов для временных сигналов:
y(t, a, b) = (Kn/ 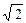 ) yn(x), x=(t-b)/a, K1=1.062, K2=0.867, K3 =0.548, K4=0.293.
) yn(x), x=(t-b)/a, K1=1.062, K2=0.867, K3 =0.548, K4=0.293.
Для сужения базовой формы вейвлетов применяется также упрощенная форма:
yn(x) = (-1)n+1 dn[exp(-x2)]/dxn, n ≥ 1, (2.1.1')
WАVE-вейвлетвычисляется по первой производной (n=1) и приведен на рис. 2.1.3 во временной и частотной области для трех значений масштабных коэффициентов 'а'. Форма вейвлета относится к нечетным функциям и, соответственно, спектр вейвлета является мнимым. Уравнение вейвлета по (2.1.1') с единичной нормой:
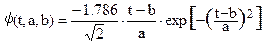 . (2.1.2)
. (2.1.2)
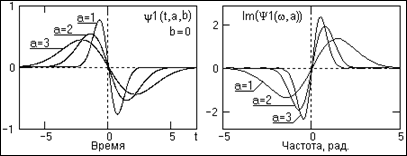 Рис. 2.1.3. Вейвлет Wave. Рис. 2.1.3. Вейвлет Wave. |
На рис. 2.1.4 приведен пример применения вейвлета для анализа двух однотипных сигналов, один из которых осложнен шумами с мощностью на уровне мощности самого сигнала. Как следует из рисунка, контурная масштабно-временная картина вейвлетных коэффициентов, а равно и ее сечения на больших значениях масштабных коэффициентов 'а' (малых доминирующих частотах вейвлетов) очень точно и уверенно фиксирует положение вершины информационного сигнала сменой знака коэффициентов с(a,b).
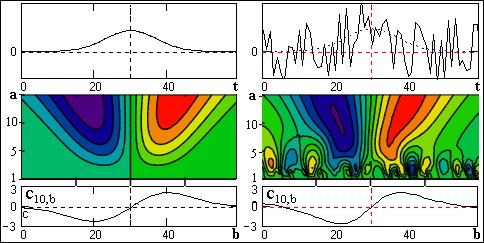
Рис. 2.1.4.
МНАТ-вейвлет (Mexican hat – мексиканская шляпа) вычисляется по второй производной (n=2) и приведен на рис. 2.1.5. Вейвлет симметричен, спектр вейвлета представлен только действительной частью и хорошо локализован по частоте, нулевой и первый моменты вейвлета равны нулю. Применяется для анализа сложных сигналов. Уравнение вейвлета по (2.1.1'):
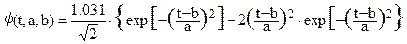 . (2.1.3)
. (2.1.3)
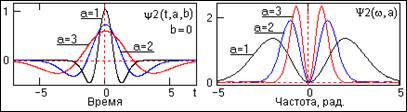
Рис. 2.1.5. Вейвлет MHAT.
На рис. 2.1.6 приведен пример использования вейвлета для анализа сложного сигнала y(t). Модель сигнала образована суммой сигналов разной структуры. Сигналы у1-у2 представляют собой функции Гаусса разного масштабного уровня, сигнал у3 - прямоугольный импульс, сигнал у4 задан в виде тренда с постоянным значением дифференциала. На контурном графике вейвлет-коэффициентов можно видеть выделение всех трех основных структур сигнала при полном исключении тренда. Особенно четко выделяются границы скачков прямоугольной структуры. Справа на рисунке приведена полная трехмерная картина вейвлет-преобразования.
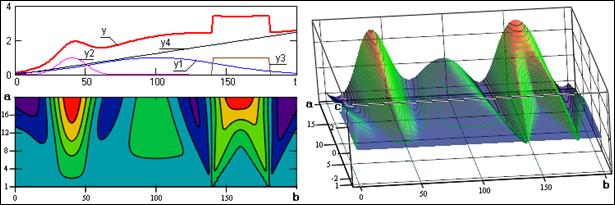
Рис. 2.1.6.
Вейвлет широко используется в двумерном варианте для анализа изотропных полей. На его основе возможно также построение двумерного неизотропного базиса с хорошей угловой избирательностью при добавлении к сдвигам и масштабированию вейвлета его вращения.
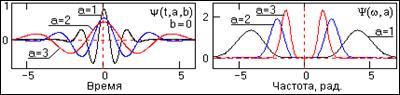 Рис. 2.1.7. Рис. 2.1.7. |
При повышении номера производной функции (2.1.1) временная область определения вейвлета несколько увеличивается при достаточно существенном повышении доминирующей частоты вейвлета и степени его локализации в частотной области. Вейвлеты n-го порядка позволяют анализировать более тонкие высокочастотные структуры сигналов, подавляя низкочастотные компоненты. Пример вейвлета по восьмой производной приведен на рис. 2.1.7.
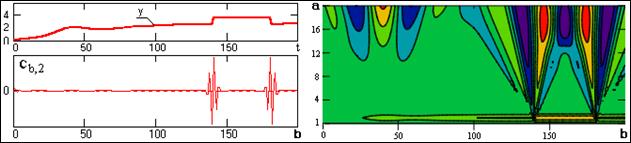
Рис. 2.1.8.
Практическое следствие повышения степени локализации вейвлетов в частотной области наглядно видно на рис. 2.1.8 на примере преобразования той же функции, что и на рис. 2.1.6. Сравнение рисунков показывает существенное повышение чувствительности вейвлета к высокочастотным составляющим сигнала на малых масштабных коэффициентах.
