Вейвлет-преобразование простых сигналов

Вейвлет-преобразование, выполняемое при анализе сигналов для выявления в них каких-либо особенностей и места их локализации без обратной реконструкции, допускает применение любых типов вейвлетов, как ортогональных, так и неортогональных. Чаще всего для этих целей используются симметричные вейвлеты типа Mhat. Ниже приводятся результаты применения вейвлета Mhat для анализа сигналов простых форм. Вычисления выполнены с вейвлетом (2.1.3) по формуле:

с(a,b) = 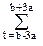s(t) y(t,a,b), (2.3.1)

где суммирование выполняется в растворе угла влияния (по области достоверности) с шагом Dt = Db = Da = 1. Так как при непрерывном разложении скейлинг-функция не используется, отсчет значений 'а' начинается с 1, а ряд коэффициентов c(0,b) оставляется нулевым и определяет нулевой фон контурных графиков спектра.

Импульсы Кронекера (положительный и отрицательный), вейвлет-спектр импульсов и сечения спектра на трех значениях параметра 'а' приведены на рис. 2.3.1. Цветовая гамма спектра здесь и в дальнейшем соответствует естественному цветоряду от красного (большие значения) к фиолетовому (малые значения коэффициентов).

Рис. 2.3.1. Преобразование импульсов Кронекера.

На сечениях спектра видно, что свертка единичных импульсов с разномасштабными вейвлетами повторяет форму вейвлетов, как это и положено при операции свертки. Соответственно, линии максимальных экстремумов на сечениях ("хребты" и "долины", в зависимости от полярности) определяют временное положение импульсов, а боковые экстремумы противоположной полярности образуют характерные лепестки в конусе угла влияния, который хорошо выражен.

Рис. 2.3.2. Преобразование функций Лапласа.

Аналогичный характер спектра сохраняется и для любых локальных неоднородностей на сигналах в форме пиков (рис. 2.3.2) со смещением максимумов (минимумов) коэффициентов с(a,b) со значений а=1 в область больших значений 'а' (в зависимости от эффективной ширины пиков).

Рис. 2.3.3. Преобразование функций Гаусса.

На рис. 2.3.3 приведен спектр функций Гаусса. При сглаживании вершин пиковых неоднородностей форма цветовых конусов также сглаживается, но "хребтовые" ("долинные") линии достаточно точно фиксируют на временной оси положение центров локальных неоднородностей.

Рис. 2.3.4. Преобразование перепада постоянного значения функций.

На рис. 2.3.4 приведены спектры двух разных по крутизне перепадов постоянных значений функции. Центры перепадов фиксируются по переходу через нуль значений коэффициентов c(a,b), а крутизна перепадов отражается, в основном, на значениях функции c(a,b) при малых значениях параметра 'а'.

При изломах функций спектрограммы уверенно фиксируют место изломов максимумами (минимумами) значений коэффициентов c(a,b), как это показано на рис. 2.3.5. При наложении на такие функции шумов точное определение места изломов по масштабным сечениям на малых значениях параметра 'а' становится невозможным, однако на больших значениях параметра 'а' такая возможность сохраняется, естественно, с уменьшением точности локализации.

Рис. 2.3.5. Преобразование изломов функций.

Аналогичный характер имеет влияние шумов и на другие локальные сигналы, приведенные на рис. 2.3.1-2.3.4, и если спектральные особенности сигналов достаточно глубоки по диапазону значений параметра 'а', то остается возможность идентификации этих локальных сигналов и их места на временной оси.

Рис. 2.3.6. Преобразование гармонических функций.

Разделение гармонических функций на масштабной оси спектров, в том числе при наложении сильных шумовых процессов, приведено в примерах на рис. 2.3.6. Приведенный пример имеет чисто иллюстративный характер, так как для выделения гармонических процессов с постоянной частотой во времени целесообразно использовать спектральный анализ и частотные полосовые фильтры. Тем не менее, для локальных сигналов, типа модулированных гармоник, вейвлет-спектры достаточно хорошо показывают место их локализации на временной оси.

Рис. 2.3.7. Изменение фазы гармонического сигнала.

На рис. 2.3.7 приведен пример еще одной характерной особенности гармонического сигнала – изменение его фазы на 180^о, которое хорошо фиксируется на всех масштабах вейвлета, а, следовательно, достаточно легко определяется даже в присутствии сильных шумовых сигналов.

При наложении синусоидальных сигналов на тренд вейвлет-преобразование на больших масштабах позволяет достаточно уверенно выделять характерные особенности тренда. Пример выделения изломов тренда приведен на рис. 2.3.8.

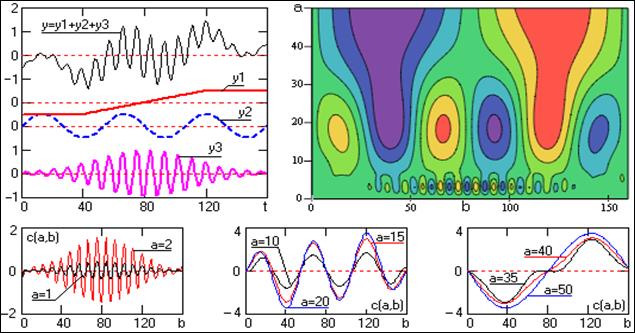
Рис. 2.3.8. Преобразование суммы трех сигналов.

Форма вейвлета (четность или нечетность), доминирующая частота и степень ее локализации существенно влияют на вейвлет-спектры анализируемых сигналов и на возможности выделения его локальных особенностей. На нижеследующих рисунках приведены сравнительные спектры простых сигналов при использовании вейвлетов Wave (нечетный, рис. 2.1.3), Mhat (четный, рис. 2.1.5) и вейвлета по 8-й производной Гаусса (рис. 2.3.9-2.3.16), который также является четным, и имеет в 4 раза более высокую доминирующую частоту, чем вейвлет Mhat.

Рис. 2.3.9. Импульсы Кронекера.

Рис. 2.3.10. Пики Лапласа.

Рис. 2.3.11. Функции Гаусса.

Рис. 2.3.12. Крутые скачки.

Рис. 2.3.13. Сглаженные скачки.

Рис. 2.3.14. Изломы функций

Рис. 2.3.15. Фазовые скачки гармоник.

Рис. 2.3.16. Сумма двух модулированных синусоид.

Заметим, что при анализе произвольных сигналов использование разнотипных вейвлетов позволяет повысить достоверность выделения локальных особенностей сигналов.

литература

1. Астафьева Н.М. Вейвлет-анализ: Основы теории и примеры применения. – Успехи физических наук, 1996, т.166, № 11, стр. 1145-1170.

3. Дьяконов В., Абраменкова И. MATLAB. Обработка сигналов и изображений. Специальный справочник. – СПб.: Питер, 2002, 608 с.

А.В.Давыдов.

26.04.08.

Cайт автора Лекции Практикум

О замеченных ошибках и предложениях по дополнению: [email protected].

Copyright ©2008 Davydov А.V.