Графики тригонометрических функций
Тема: «Методика изучения тригонометрических функций»
В лекции использованы материалы из лекций проф. Ананченко К.О.
 §1 Содержание темы. Перечень знаний и умений по теме.
§1 Содержание темы. Перечень знаний и умений по теме.
Тригонометрия — один из наиболее важных разделов курса алгебры и начал анализа.
Он включает изучениеследующих вопросов:
- введение тригонометрических функций числового аргумента и их простейшие свойства;
- тригонометрические тождества;
- тригонометрические уравнения и неравенства.
Содержание темы по классам:
Класс
- Периодичность функции. Функции y=sin x, y=cos x, 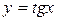 , их свойства и графики.
, их свойства и графики.
- Простейшие тригонометрические уравнения sin x=а, cos x=а, 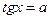 . Тригонометрические уравнения.
. Тригонометрические уравнения.
Тригонометрические функции – класс элементарных функции: синус, косинус, тангенс, котангенс, секанс, косеканс. Они предоставляют удобный аппарат для решения разнообразных геометрических задач. Тригонометрические функции имеют многочисленные приложения в астрономии, геодезии, механике, электротехнике и других науках.
В результате изучения темы “ Тригонометрические функции ” учащиеся должны:
знать определения тригонометрических функций, определение периодической функции, формулировку и доказательство теоремы о периодичности тригонометрических функций, наименьший положительный период для функций синус, косинус, тангенс, котангенс;
уметь исследовать тригонометрические функции на четность и нечётность; применять свойство периодичности тригонометрических функций при вычислении их значений и построении их графиков; уметь по графику находить область определения и область значений, промежутки возрастания и убывания, нули, экстремумы данных функций.
§  2 Определение тригонометрических функций
2 Определение тригонометрических функций
Пусть М-точка окружности с центром в начале координат и радиусом, равным единице; a- угол между осью абсцисс и радиусом ОМ, отсчитываемый от положительного направления оси абсцисс (рис. 18). При этом если отсчёт ведётся против часовой стрелки, то величина угла считается положительной, а если по часовой стрелке – отрицательной. Если (Хa ; Ya) – координаты точки М, то тригонометрические функции синус и косинус определяются формулами :
sin a= Ya ; cos a= Хa
Другие тригонометрические функции определяются формулами :
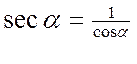
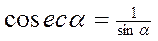
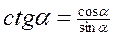
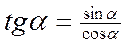


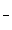

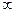
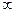 Угол может измеряться как в градусах, так и в радианах и изменяться от - до + . Чаще используется радианное измерение, причём обозначение радиан опускается, и тогда тригонометрические функции считаются функциями числового аргумента.
Угол может измеряться как в градусах, так и в радианах и изменяться от - до + . Чаще используется радианное измерение, причём обозначение радиан опускается, и тогда тригонометрические функции считаются функциями числового аргумента.
В методической литературе предлагаются различные подходы к определению тригонометрических функций. Функции синус и косинус рассматриваются:
 как отношение сторон в прямоугольном треугольнике для острых углов с последующим распространением на любые углы;
как отношение сторон в прямоугольном треугольнике для острых углов с последующим распространением на любые углы;
 как координаты точек единичной окружности или координаты конца подвижного единичного радиуса;
как координаты точек единичной окружности или координаты конца подвижного единичного радиуса;
 как отношение координат конца подвижного радиуса некоторой окружности к длине этого радиуса;
как отношение координат конца подвижного радиуса некоторой окружности к длине этого радиуса;
 как отношение координат конца радиуса-вектора к его длине;
как отношение координат конца радиуса-вектора к его длине;
 как проекции единичного вектора на оси координат;
как проекции единичного вектора на оси координат;
 как отношения проекций вектора на векторные оси к длине указанного вектора.
как отношения проекций вектора на векторные оси к длине указанного вектора.
Графики тригонометрических функций
В методической литературе для построения графиков тригонометрических функций рекомендуются различные подходы. Рассмотрим некоторые из них на примере функций y=sin x.
1. Сначала предлагается построить часть графика функции синус на отрезке [0:p] по точкам:
| x | 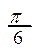 | 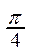 | 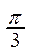 | 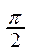 | 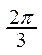 | 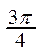 | 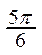 | p | |
| sin x | 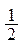 | 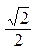 | 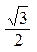 | 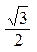 | 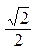 | 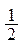 |
Затем воспользовавшись свойством нечётности функции синус, можно построить график функции на отрезке:[- p;0] и продолжить его периодичность на всю ось OX (рис.19)
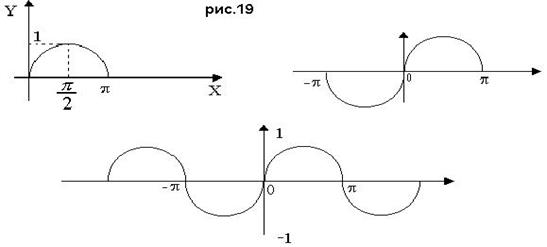 |
2. Существует другой способ построения графика функции y=sin x. Строится единичная окружность и делится на 12 равных дуг, концы которых будут соответствовать значениям аргумента, указанным в таблице:
| x | 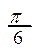 | 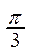 | 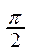 | 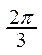 | 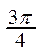 | 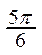 | p | 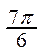 | 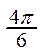 | 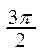 | 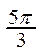 | 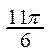 | 2p | |
| sin x | 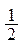 | 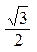 | 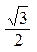 | 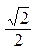 | 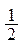 | 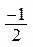 | 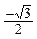 | -1 | 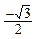 | 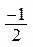 |
Дальнейшее построение графика y = sin x ясно из рассмотрения рис.
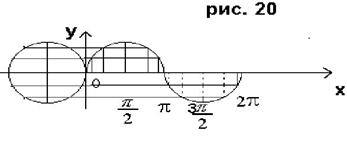 |
Так как наименьший положительный период синуса равен 2p, то график функции y=sin x в промежутке от -2p до 0 будет иметь такой же вид, как и в промежутке от 0 до 2p, то же верно для промежутка от 2p до 4p и т.д.
Исходя из геометрических соображений можно построить график тригонометрической функции с любой степенью точности, что зависит от числа делений, на которые делится окружность с радиусом, равным единице.
3. Для построения графика синуса проводится её исследование с помощью производной на любом отрезке длины 2p, например, на отрезке [-p;p]. Находятся производная функции синус и критические точки функции, а затем заполняется таблица:
| x | -p | 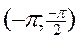 | 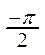 | 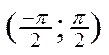 | 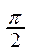 | 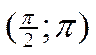 | p | |
| sin x | -1 | - | + | - | -1 | |||
| sin x | -1 | |||||||
| min | max | |||||||
Пользуясь проведённым исследованием, строят график функции y=sin x на отрезке [-p;p], а затем на всей оси OX.
Задание для самостоятельного изучения
1) Ознакомьтесь с действующим учебным пособием “АиНА” и установите, какой способ используется при построении графика функции y=sin x.
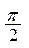 2) Подумайте, с помощью каких преобразований из графика функции y=sin x можно получить график функции y=-2sin(x- )+1.
2) Подумайте, с помощью каких преобразований из графика функции y=sin x можно получить график функции y=-2sin(x- )+1.
Для закрепления навыка построения графиков тригонометрических функций с помощью простейших преобразований графиков рекомендуется провести лабораторную работу на тему “Построение графиков тригонометрических функций”.
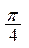
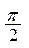
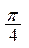 Вариант 1. С использованием шаблона вычертите графики: y=sin x , y=sin x -1 , y=sin(x- ) , y=sin(x+ ).
Вариант 1. С использованием шаблона вычертите графики: y=sin x , y=sin x -1 , y=sin(x- ) , y=sin(x+ ).
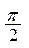 Вариант 2. С использованием шаблона вычертите графики функций : y=cos x , y=cos x+2, y=cos(x+ ) , y=cos(x- ).
Вариант 2. С использованием шаблона вычертите графики функций : y=cos x , y=cos x+2, y=cos(x+ ) , y=cos(x- ).
§4 Свойства и график функции y = sin x
1. Область определения – множество всех действительных чисел.
2. Область значений – отрезок [-1; 1].
3. Функция нечётная.
4. Функция периодическая, основной период равен 2 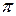 .
.
5. Функция возрастает на промежутках [ 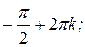
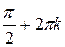 ] и убывает на промежутках [
] и убывает на промежутках [ 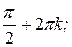
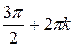 ], k
], k 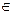 Z
Z
6. В точках 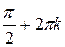 (k
(k 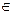 Z) синус имеет максимумы, равные 1; в точках
Z) синус имеет максимумы, равные 1; в точках 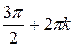 - минимумы, равные –1.
- минимумы, равные –1.
График функции y = sin x изображён на рис. 21.
                y 0 x y 0 x 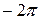 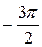 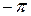 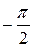 1 1 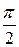 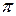 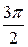 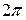 |
рис.21
§5 Свойства и график функции y = cos x.
1. Область определения функции – множество всех действительных чисел.
2. Область значений – отрезок [-1; 1].
3. Функция чётная.
4. Функция периодическая с основным периодом 2 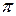 .
.
5. Функция возрастает на промежутках [ 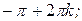
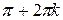 ] и убывает на промежутках [
] и убывает на промежутках [ 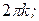
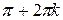 ], k
], k 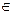 Z
Z
6. Косинус имеет максимумы, равные 1, в точках x = 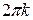 , k
, k 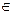 Z; косинус имеет минимумы, равные –1, в точках x =
Z; косинус имеет минимумы, равные –1, в точках x = 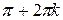 , k
, k 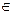 Z.
Z.
График функции y = cos x изображён на рис. 22.
                  y 0 x y 0 x 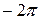 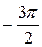 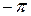 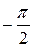 -1 -1 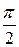 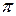 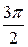 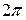 |
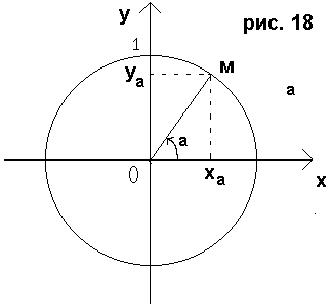
§6 Свойства и график функции 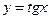
1. Область определения – множество всех действительных чисел, кроме числе вида 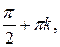 где k Î Z.
где k Î Z.
2. Область определения – вся числовая прямая.
3. Функция нечётная.
4. π – основной период функции.
5. Функция возрастает на промежутках (-π/2 + πk, π/2 + πk), где k Î Z.
6. Функция не имеет экстремумов.
7. График функции 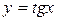 изображён на рисунке 23.
изображён на рисунке 23.