Тема 2. Характеристики продолжительности жизни
Задача 2.1. Используя таблицу смертности, вычислить вероятность для тридцатилетнего мужчины не дожить до 60 лет.
Решение.
Вероятность для человека возраста 
лет умереть в течение ближайших 
лет равна
.
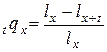Тогда искомая вероятность
.
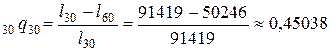Задача 2.2.Рассмотрим семейную пару, в которой жене 30 лет, а мужу 37 лет. Какова вероятность того, что они проживут еще по крайней мере 30 лет?
Решение.
Искомая вероятность представляет собой произведение вероятностей событий «жена проживет по крайней мере 30 лет» и «муж проживет по крайней мере 30 лет». Тогда
.
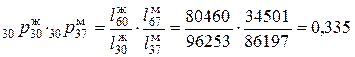Задача 2.3.Функция выживания задана формулой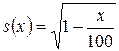 
, 
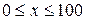. Найти:
a) интенсивность смертности в возрасте 30 лет;
b) вероятность того, что человек возраста 40 лет умрет в возрасте от 60 до 65 лет.
Решение.
a) Интенсивность смертности равна
.
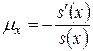Тогда
;
.
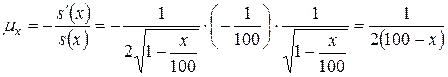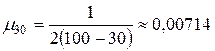b) Вероятность того, что человек возраста лет проживет еще лет, но умрет на протяжении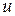 
последующих лет, равна
.
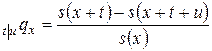Тогда искомая вероятность равна
.
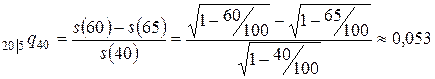Задача 2.4.Интенсивность смертности имеет вид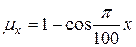 
. Найти функцию выживания 
.
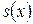Решение.
Функция выживания через интенсивность смертности определяется по формуле
.
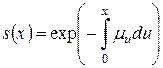Тогда
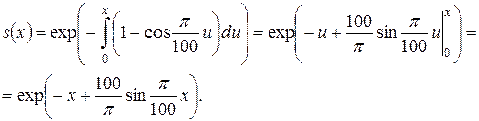
Задача 2.5.Кривая смертей имеет вид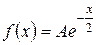 
. Найти:
a) функцию выживания ;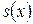
b) дисперсию времени жизни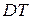 
.
Решение.
a) Найдем неизвестный коэффициент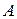 
из условия
.
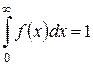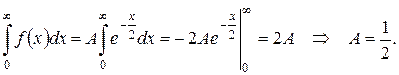
Функция выживания
.
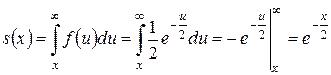b) Дисперсия времени жизни вычисляется по формуле
.
.
.
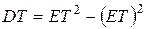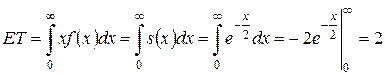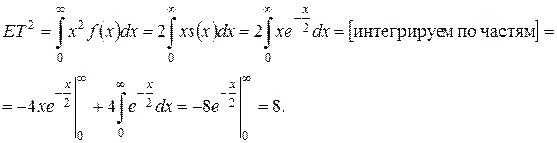
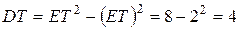Задача 2.6. Найти вероятность того, что 50-летний мужчина проживет еще полгода после своего дня рождения при предположении:
a) равномерного распределения смертей;
b) Балдуччи.
Решение.
a) В предположении равномерного распределения смертей искомая вероятность равна
.
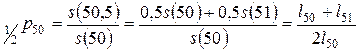Используя данные таблицы смертности, получим
.
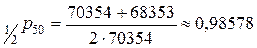b) В предположении Балдуччи искомая вероятность равна
.
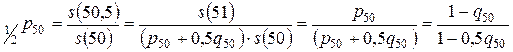Используя данные таблицы смертности, получим
.
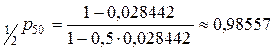Тема 3. Теория страхования на основе использования таблиц продолжительности жизни и связанных с этими таблицами характеристик и функций
Задача 3.1.Известно, что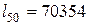 
, 
, 
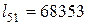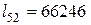, эффективная годовая процентная ставка 
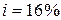. Возраст человека на момент заключения договора 50 лет. Найти актуарную современную стоимость трехлетней временной пожизненной ренты, выплачиваемой раз в год в начале года в размере 50000 рублей.
Решение.
Актуарная современная стоимость временной пожизненной ренты, выплачиваемой раз в год в начале года для суммы в одну денежную единицу равна
,
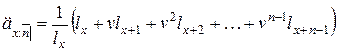где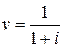 
– коэффициент дисконтирования.
Тогда искомая величина, обозначим ее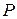 
, равна
.
.
.
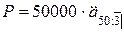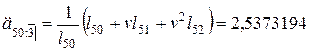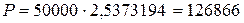Задача 3.2.Родители семилетней девочки оформляют договор на оплату высшего образования ребенка, по достижению им 18 лет. Срок обучения 5 лет, стоимость 90000 рублей в год. Эффективная процентная ставка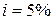 
. Найти стоимость полиса.
Решение.
Стоимость полиса равна
,
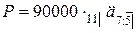Где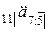 
– актуарная современная стоимость отложенной временной пожизненной ренты, выплачиваемой раз в год в начале года для суммы в одну денежную единицу.
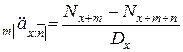– отложенная на 
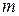лет временная пожизненная рента для человека возраста лет, выраженная через коммутационные числа 
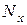и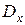 
(эти числа находят по таблице коммутационных чисел).
Тогда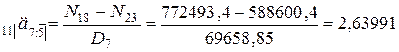 
.
.
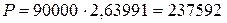Задача 3.3.Мужчина в возрасте 45 лет покупает за 120000 рублей пожизненную ренту (пенсию), выплаты которой начинаются с возраста 65 лет. Эффективная процентная ставка 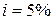. Найти величину ежегодных выплат.
Решение.
Величина ежегодных выплат, обозначим ее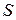 
, равна
.
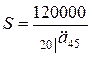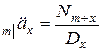– актуарная современная стоимость отложенной пожизненной ренты, выраженная через коммутационные числа 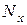и 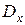(эти числа находят по таблице коммутационных чисел).
.
.
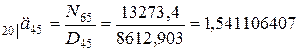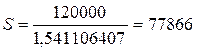Задача 3.4.Мужчина в возрасте 50 лет приобрел пожизненный страховой полис, по которому в случае его смерти наследники должны получить 100000 рублей. Эффективная процентная ставка 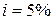. Найти стоимость полиса.
Решение.
Стоимость полиса, обозначим ее 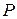, равна
.
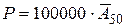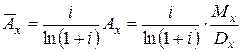– ожидаемая текущая стоимость страховых выплат, осуществляемых в момент смерти, для пожизненного страхования.
.
.
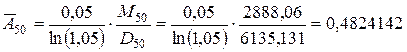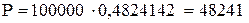Задача 3.5. Мужчина в возрасте 60 лет приобрел пожизненную ренту с выплатой 40000 рублей в конце каждого года. Эффективная процентная ставка 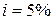. Найти стоимость полиса.
Решение.
Стоимость полиса, обозначим ее 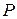, равна
.
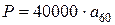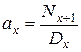– актуарная современная стоимость пожизненной ренты, выраженная через коммутационные числа 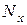и 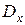(эти числа находят по таблице коммутационных чисел).
.
.
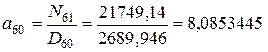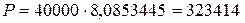Задача 3.6. Страхователь в возрасте 40 лет заключил договор, согласно которому, начиная с 65 лет, пожизненно будет выплачиваться пенсия в размере 50000 рублей в начале каждого года. Эффективная процентная ставка 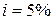. Найти величину годовых взносов, которые будут уплачиваться страхователем с 40 до 65 лет.
Решение.
Искомая величина годовых взносов, обозначим ее 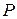, равна
.
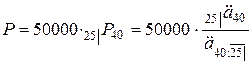Где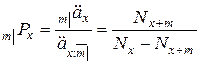 
– величина ежегодного взноса, рассчитанная на сумму в одну условную единицу.
.
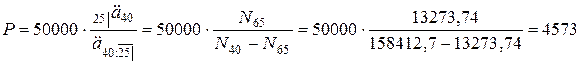Задача 3.7. Мужчина в возрасте 40 лет покупает за 100000 рублей пожизненную ренту (пенсию), выплаты которой начинаются с возраста 65 лет. Эффективная процентная ставка 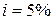. Найти величину ежегодных выплат.
Решение.
Искомая величина ежегодных выплат равна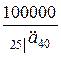 
,
где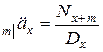 
– актуарная современная стоимость пожизненной отложенной ренты.
.
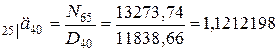Тогда величина ежегодных выплат равна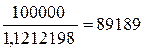 
.
Задача 3.8.Страхователь (женщина) в возрасте 47 лет заключил пожизненный договор страхования с условием ежегодной уплаты взносов, пока он жив. Страховая сумма составляет 150000 рублей, эффективная процентная ставка 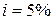. Найти величину годовых взносов.
Решение.
Искомая величина годовых взносов равна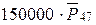 
,
где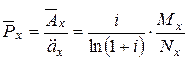 
– величина годового взноса с единичной страховой суммы.
.
Величина годовых взносов тогда равна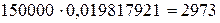 
.
Задача 3.9.Родители пятилетнего мальчика приобрели полис по оплате получения ребенком высшего образования по достижению им 18 лет. Срок обучения 5 лет, стоимость 110000 рублей в год. Эффективная процентная ставка 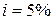. Найти величину ежегодных взносов.
Решение.
Искомая величина ежегодных взносов равна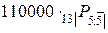 
,
где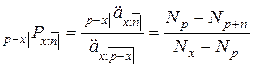 
– величина ежегодного взноса для отложенной срочной ренты.
.
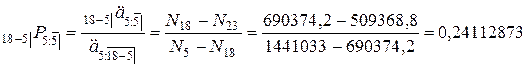Тогда величина ежегодных взносов равна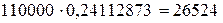 
.